湖北省武汉市2021年中考数学试卷
试卷更新日期:2021-06-24 类型:中考真卷
一、单选题
-
1. 3的相反数是( )A、 3 B、-3 C、 D、2. 下列事件中是必然事件的是( )A、抛掷一枚质地均匀的硬币,正面朝上 B、随意翻到一本书的某页,这一页的页码是偶数 C、打开电视机,正在播放广告 D、从两个班级中任选三名学生,至少有两名学生来自同一个班级3. 下列图形都是由一个圆和两个相等的半圆组合而成的,其中既是轴对称图形又是中心对称图形的是( )A、

B、
B、
C、
C、
D、
D、
4. 计算 的结果是( )A、 B、 C、 D、5. 如图是由4个相同的小正方体组成的几何体,它的主视图是( )
4. 计算 的结果是( )A、 B、 C、 D、5. 如图是由4个相同的小正方体组成的几何体,它的主视图是( ) A、
A、 B、
B、 C、
C、 D、
D、 6. 学校招募运动会广播员,从两名男生和两名女生共四名候选人中随机选取两人,则两人恰好是一男一女的概率是( )A、 B、 C、 D、7. 我国古代数学名著《九章算术》中记载:“今有共买物,人出八,盈三;人出七,不足四,问人数,物价各几何?”意思是现有几个人共买一件物品,每人出8钱.多出3钱;每人出7钱,差4钱.问人数,物价各是多少?若设共有 人,物价是 钱,则下列方程正确的是( )A、 B、 C、 D、8. 一辆快车和一辆慢车将一批物资从甲地运往乙地,其中快车送达后立即沿原路返同,且往返速度的大小不变,两车离甲地的距离 (单位: )与慢车行驶时间 (单位: )的函数关系如图,则两车先后两次相遇的间隔时间是( )
6. 学校招募运动会广播员,从两名男生和两名女生共四名候选人中随机选取两人,则两人恰好是一男一女的概率是( )A、 B、 C、 D、7. 我国古代数学名著《九章算术》中记载:“今有共买物,人出八,盈三;人出七,不足四,问人数,物价各几何?”意思是现有几个人共买一件物品,每人出8钱.多出3钱;每人出7钱,差4钱.问人数,物价各是多少?若设共有 人,物价是 钱,则下列方程正确的是( )A、 B、 C、 D、8. 一辆快车和一辆慢车将一批物资从甲地运往乙地,其中快车送达后立即沿原路返同,且往返速度的大小不变,两车离甲地的距离 (单位: )与慢车行驶时间 (单位: )的函数关系如图,则两车先后两次相遇的间隔时间是( )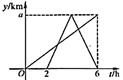 A、 B、 C、 D、9. 如图, 是 的直径, 是 的弦,先将 沿 翻折交 于点 .再将 沿 翻折交 于点 .若 ,设 ,则 所在的范围是( )
A、 B、 C、 D、9. 如图, 是 的直径, 是 的弦,先将 沿 翻折交 于点 .再将 沿 翻折交 于点 .若 ,设 ,则 所在的范围是( )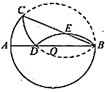 A、 B、 C、 D、10. 已知 , 是方程 的两根,则代数式 的值是( )A、-25 B、-24 C、35 D、36
A、 B、 C、 D、10. 已知 , 是方程 的两根,则代数式 的值是( )A、-25 B、-24 C、35 D、36二、填空题
-
11. 计算 的结果是12. 我国是一个人口资源大国,第七次全国人口普查结果显示,北京等五大城市的常住人口数如下表,这组数据的中位数是.
城市
北京
上海
广州
重庆
成都
常住人口数/万
2 189
2 487
1 868
3 205
2 094
13. 已知点 , 在反比例函数 ( 是常数)的图象上,且 ,则 的取值范围是.14. 如图,海中有一个小岛 ,一艘轮船由西向东航行,在 点测得小岛 在北偏东 方向上;航行 到达 点,这时测得小岛 在北偏东 方向上.小岛 到航线 的距离是 ( ,结果用四舍五入法精确到0.1).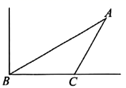 15. 已知抛物线 ( , , 是常数), ,下列四个结论:
15. 已知抛物线 ( , , 是常数), ,下列四个结论:①若抛物线经过点 ,则 ;
②若 ,则方程 一定有根 ;
③抛物线与 轴一定有两个不同的公共点;
④点 , 在抛物线上,若 ,则当 时, .
其中正确的是(填写序号).
16. 如图(1),在 中, , ,边 上的点 从顶点 出发,向顶点 运动,同时,边 上的点 从顶点 出发,向顶点 运动, , 两点运动速度的大小相等,设 , , 关于 的函数图象如图(2),图象过点 ,则图象最低点的横坐标是.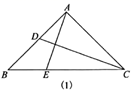

三、解答题
-
17. 解不等式组 请按下列步骤完成解答.(1)、解不等式①,得;(2)、解不等式②,得;(3)、把不等式①和②的解集在数轴上表示出来;
 (4)、原不等式组的解集是.18. 如图, , ,直线 与 , 的延长线分别交于点 , .求证: .
(4)、原不等式组的解集是.18. 如图, , ,直线 与 , 的延长线分别交于点 , .求证: . 19. 为了解落实国家《关于全面加强新时代大中小学劳动教育的意见》的实施情况,某校从全体学生中随机抽取部分学生,调查他们平均每周劳动时间 (单位: ),按劳动时间分为四组: 组“ ”, 组“ ”, 组“ ”, 组“ ”.将收集的数据整理后,绘制成如下两幅不完整的统计图.
19. 为了解落实国家《关于全面加强新时代大中小学劳动教育的意见》的实施情况,某校从全体学生中随机抽取部分学生,调查他们平均每周劳动时间 (单位: ),按劳动时间分为四组: 组“ ”, 组“ ”, 组“ ”, 组“ ”.将收集的数据整理后,绘制成如下两幅不完整的统计图.

根据以上信息,解答下列问题:
(1)、这次抽样调查的样本容量是 , 组所在扇形的圆心角的大小是;(2)、将条形统计图补充完整;(3)、该校共有1500名学生,请你估计该校平均每周劳动时间不少于 的学生人数.20. 如图是由小正方形组成的 网格,每个小正方形的顶点叫做格点,矩形 的四个顶点都是格点.仅用无刻度的直尺在给定网格中完成画图,画图过程用虚线表示. (1)、在图(1)中,先在边 上画点 ,使 ,再过点 画直线 ,使 平分矩形 的面积;(2)、在图(2)中,先画 的高 ,再在边 上画点 ,使 .21. 如图, 是 的直径, 是 上两点, 是 的中点,过点 作 的垂线,垂足是 .连接 交 于点 .
(1)、在图(1)中,先在边 上画点 ,使 ,再过点 画直线 ,使 平分矩形 的面积;(2)、在图(2)中,先画 的高 ,再在边 上画点 ,使 .21. 如图, 是 的直径, 是 上两点, 是 的中点,过点 作 的垂线,垂足是 .连接 交 于点 . (1)、求证: 是 的切线;(2)、若 ,求 的值.22. 在“乡村振兴”行动中,某村办企业以 , 两种农作物为原料开发了一种有机产品, 原料的单价是 原料单价的1.5倍,若用900元收购 原料会比用900元收购 原料少 .生产该产品每盒需要 原料 和 原料 ,每盒还需其他成本9元.市场调查发现:该产品每盒的售价是60元时,每天可以销售500盒;每涨价1元,每天少销售10盒.(1)、求每盒产品的成本(成本=原料费+其他成本);(2)、设每盒产品的售价是 元( 是整数),每天的利润是 元,求 关于 的函数解析式(不需要写出自变量的取值范围);(3)、若每盒产品的售价不超过 元( 是大于60的常数,且是整数),直接写出每天的最大利润.23. 问题提出 如图(1),在 和 中, , , ,点 在 内部,直线 与 交于点 ,线段 , , 之间存在怎样的数量关系?
(1)、求证: 是 的切线;(2)、若 ,求 的值.22. 在“乡村振兴”行动中,某村办企业以 , 两种农作物为原料开发了一种有机产品, 原料的单价是 原料单价的1.5倍,若用900元收购 原料会比用900元收购 原料少 .生产该产品每盒需要 原料 和 原料 ,每盒还需其他成本9元.市场调查发现:该产品每盒的售价是60元时,每天可以销售500盒;每涨价1元,每天少销售10盒.(1)、求每盒产品的成本(成本=原料费+其他成本);(2)、设每盒产品的售价是 元( 是整数),每天的利润是 元,求 关于 的函数解析式(不需要写出自变量的取值范围);(3)、若每盒产品的售价不超过 元( 是大于60的常数,且是整数),直接写出每天的最大利润.23. 问题提出 如图(1),在 和 中, , , ,点 在 内部,直线 与 交于点 ,线段 , , 之间存在怎样的数量关系?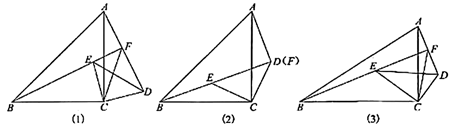 (1)、问题探究:先将问题特殊化.如图(2),当点 , 重合时,直接写出一个等式,表示 , , 之间的数量关系;(2)、再探究一般情形.如图(1),当点 , 不重合时,证明(1)中的结论仍然成立.(3)、问题拓展 如图(3),在 和 中, , , ( 是常数),点 在 内部,直线 与 交于点 ,直接写出一个等式,表示线段 , , 之间的数量关系.24. 抛物线 交 轴于 , 两点( 在 的左边).
(1)、问题探究:先将问题特殊化.如图(2),当点 , 重合时,直接写出一个等式,表示 , , 之间的数量关系;(2)、再探究一般情形.如图(1),当点 , 不重合时,证明(1)中的结论仍然成立.(3)、问题拓展 如图(3),在 和 中, , , ( 是常数),点 在 内部,直线 与 交于点 ,直接写出一个等式,表示线段 , , 之间的数量关系.24. 抛物线 交 轴于 , 两点( 在 的左边).
 (1)、 的顶点 在 轴的正半轴上,顶点 在 轴右侧的抛物线上.
(1)、 的顶点 在 轴的正半轴上,顶点 在 轴右侧的抛物线上.①如图(1),若点 的坐标是 ,点 的横坐标是 ,直接写出点 , 的坐标;
②如图(2),若点 在抛物线上,且 的面积是12,求点 的坐标;
(2)、如图(3), 是原点 关于抛物线顶点的对称点,不平行 轴的直线 分别交线段 , (不含端点)于 , 两点,若直线 与抛物线只有一个公共点,求证 的值是定值.