四川省南充市2021年中考数学试卷
试卷更新日期:2021-06-24 类型:中考真卷
一、单选题
-
1. 满足 的最大整数 是( )A、1 B、2 C、3 D、42. 数轴上表示数 和 的点到原点的距离相等,则 为( )A、-2 B、2 C、1 D、-13. 如图,点O是 对角线的交点,EF过点O分別交AD,BC于点E,F.下列结论成立的是( )
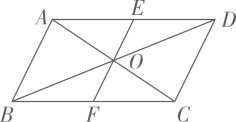 A、 B、 C、 D、4. 据统计,某班7个学习小组上周参加“青年大学习”的人数分别为:5,5,6,6,6,7,7,下列说法错误的是( )A、该组数据的中位数是6 B、该组数据的众数是6 C、该组数据的平均数是6 D、该组数据的方差是65. 端午节买粽子,每个肉粽比素粽多1元,购买10个肉粽和5个素粽共用去70元,设每个肉粽x元,则可列方程为( )A、 B、 C、 D、6. 下列运算正确的是( )A、 B、 C、 D、7. 如图,AB是 的直径,弦 于点E, ,则 的度数为( )
A、 B、 C、 D、4. 据统计,某班7个学习小组上周参加“青年大学习”的人数分别为:5,5,6,6,6,7,7,下列说法错误的是( )A、该组数据的中位数是6 B、该组数据的众数是6 C、该组数据的平均数是6 D、该组数据的方差是65. 端午节买粽子,每个肉粽比素粽多1元,购买10个肉粽和5个素粽共用去70元,设每个肉粽x元,则可列方程为( )A、 B、 C、 D、6. 下列运算正确的是( )A、 B、 C、 D、7. 如图,AB是 的直径,弦 于点E, ,则 的度数为( )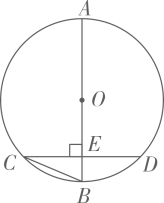 A、 B、 C、 D、8. 如图,在菱形ABCD中, ,点E,F分別在边AB,BC上, , 的周长为 ,则AD的长为( )
A、 B、 C、 D、8. 如图,在菱形ABCD中, ,点E,F分別在边AB,BC上, , 的周长为 ,则AD的长为( ) A、 B、 C、 D、9. 已知方程 的两根分别为 , ,则 的值为( )A、1 B、-1 C、2021 D、-202110. 如图,在矩形ABCD中, , ,把边AB沿对角线BD平移,点 , 分别对应点A,B.给出下列结论:①顺次连接点 , ,C,D的图形是平行四边形;②点C到它关于直线 的对称点的距离为48;③ 的最大值为15;④ 的最小值为 .其中正确结论的个数是( )
A、 B、 C、 D、9. 已知方程 的两根分别为 , ,则 的值为( )A、1 B、-1 C、2021 D、-202110. 如图,在矩形ABCD中, , ,把边AB沿对角线BD平移,点 , 分别对应点A,B.给出下列结论:①顺次连接点 , ,C,D的图形是平行四边形;②点C到它关于直线 的对称点的距离为48;③ 的最大值为15;④ 的最小值为 .其中正确结论的个数是( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 已知 ,则 =;12. 在-2,-1,1,2这四个数中随机取出一个数,其倒数等于本身的概率是.13. 如图,点E是矩形ABCD边AD上一点,点F,G,H分别是BE,BC,CE的中点, ,则GH的长为.
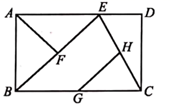 14. 若 ,则15. 如图,在 中,D为BC上一点, ,则 的值为.
14. 若 ,则15. 如图,在 中,D为BC上一点, ,则 的值为.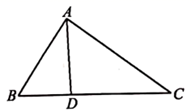 16. 关于抛物线 ,给出下列结论:①当 时,抛物线与直线 没有交点;②若抛物线与x轴有两个交点,则其中一定有一个交点在点(0,0)与(1,0)之间;③若抛物线的顶点在点(0,0),(2,0),(0,2)所围成的三角形区域内(包括边界),则 .其中正确结论的序号是.
16. 关于抛物线 ,给出下列结论:①当 时,抛物线与直线 没有交点;②若抛物线与x轴有两个交点,则其中一定有一个交点在点(0,0)与(1,0)之间;③若抛物线的顶点在点(0,0),(2,0),(0,2)所围成的三角形区域内(包括边界),则 .其中正确结论的序号是.三、解答题
-
17. 先化简,再求值: ,其中 .18. 如图, ,AD是 内部一条射线,若 , 于点E, 于点F.求证: .
 19. 某市体育中考自选项目有乒乓球、篮球和羽毛球,每个考生任选一项作为自选考试项目.(1)、求考生小红和小强自选项目相同的概率.(2)、除自选项目之外,长跑和掷实心球为必考项目.小红和小强的体育中考各项成绩(百分制)的统计图表如下:
19. 某市体育中考自选项目有乒乓球、篮球和羽毛球,每个考生任选一项作为自选考试项目.(1)、求考生小红和小强自选项目相同的概率.(2)、除自选项目之外,长跑和掷实心球为必考项目.小红和小强的体育中考各项成绩(百分制)的统计图表如下:考生
自选项目
长跑
掷实心球
小红
95
90
95
小强
90
95
95

①补全条形统计图.
②如果体育中考按自选项目占50%、长跑占30%、掷实心球占20%计算成绩(百分制),分别计算小红和小强的体育中考成绩.
20. 已知关于x的一元二次方程 .(1)、求证:无论k取何值,方程都有两个不相等的实数根.(2)、如果方程的两个实数根为 , ,且k与 都为整数,求k所有可能的值.21. 如图,反比例函数的图象与过点 , 的直线交于点B和C.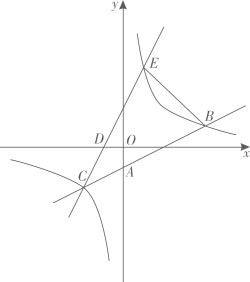 (1)、求直线AB和反比例函数的解析式.(2)、已知点 ,直线CD与反比例函数图象在第一象限的交点为E,直接写出点E的坐标,并求 的面积.22. 如图,A,B是 上两点,且 ,连接OB并延长到点C,使 ,连接AC.
(1)、求直线AB和反比例函数的解析式.(2)、已知点 ,直线CD与反比例函数图象在第一象限的交点为E,直接写出点E的坐标,并求 的面积.22. 如图,A,B是 上两点,且 ,连接OB并延长到点C,使 ,连接AC. (1)、求证:AC是 的切线.(2)、点D,E分别是AC,OA的中点,DE所在直线交 于点F,G, ,求GF的长.23. 超市购进某种苹果,如果进价增加2元/千克要用300元;如果进价减少2元/千克,同样数量的苹果只用200元.(1)、求苹果的进价.(2)、如果购进这种苹果不超过100千克,就按原价购进;如果购进苹果超过100千克,超过部分购进价格减少2元/千克.写出购进苹果的支出y(元)与购进数量x(千克)之间的函数关系式.(3)、超市一天购进苹果数量不超过300千克,且购进苹果当天全部销售完.据统计,销售单价z(元/千克)与一天销售数量x(千克)的关系为 .在(2)的条件下,要使超市销售苹果利润w(元)最大,求一天购进苹果数量.(利润=销售收入 购进支出)24. 如图,点E在正方形ABCD边AD上,点F是线段AB上的动点(不与点A重合).DF交AC于点G, 于点H, , .
(1)、求证:AC是 的切线.(2)、点D,E分别是AC,OA的中点,DE所在直线交 于点F,G, ,求GF的长.23. 超市购进某种苹果,如果进价增加2元/千克要用300元;如果进价减少2元/千克,同样数量的苹果只用200元.(1)、求苹果的进价.(2)、如果购进这种苹果不超过100千克,就按原价购进;如果购进苹果超过100千克,超过部分购进价格减少2元/千克.写出购进苹果的支出y(元)与购进数量x(千克)之间的函数关系式.(3)、超市一天购进苹果数量不超过300千克,且购进苹果当天全部销售完.据统计,销售单价z(元/千克)与一天销售数量x(千克)的关系为 .在(2)的条件下,要使超市销售苹果利润w(元)最大,求一天购进苹果数量.(利润=销售收入 购进支出)24. 如图,点E在正方形ABCD边AD上,点F是线段AB上的动点(不与点A重合).DF交AC于点G, 于点H, , .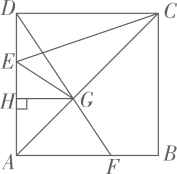 (1)、求 .(2)、设 , ,试探究y与x的函数关系式(写出x的取值范围).(3)、当 时,判断EG与AC的位置关系并说明理由.25. 如图,已知抛物线 与x轴交于点A(1,0)和B,与y轴交于点C,对称轴为 .
(1)、求 .(2)、设 , ,试探究y与x的函数关系式(写出x的取值范围).(3)、当 时,判断EG与AC的位置关系并说明理由.25. 如图,已知抛物线 与x轴交于点A(1,0)和B,与y轴交于点C,对称轴为 .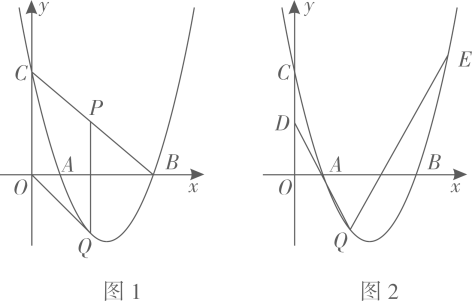 (1)、求抛物线的解析式;(2)、如图1,若点P是线段BC上的一个动点(不与点B,C重合),过点P作y轴的平行线交抛物线于点Q,连接OQ.当线段PQ长度最大时,判断四边形OCPQ的形状并说明理由.(3)、如图2,在(2)的条件下,D是OC的中点,过点Q的直线与抛物线交于点E,且 .在y轴上是否存在点F,使得 为等腰三角形?若存在,求点F的坐标;若不存在,请说明理由.
(1)、求抛物线的解析式;(2)、如图1,若点P是线段BC上的一个动点(不与点B,C重合),过点P作y轴的平行线交抛物线于点Q,连接OQ.当线段PQ长度最大时,判断四边形OCPQ的形状并说明理由.(3)、如图2,在(2)的条件下,D是OC的中点,过点Q的直线与抛物线交于点E,且 .在y轴上是否存在点F,使得 为等腰三角形?若存在,求点F的坐标;若不存在,请说明理由.