四川省成都市2021年中考数学试卷

试卷更新日期：2021-06-24 类型：中考真卷

进入出卷网下载

一、单选题

1. -7的倒数是（）

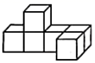
A、 $- \frac{1}{7}$ B、 $\frac{1}{7}$ C、-7 D、7

查看试题解析
2. 如图所示的几何体是由6个大小相同的小立方块搭成，它的俯视图是（）

A、 B、 C、 D、

查看试题解析
3. 2021年5月15日7时18分，天问一号探测器成功着陆距离地球逾3亿千米的神秘火星，在火星上首次留下中国人的印迹，这是我国航天事业发展的又一具有里程碑意义的进展.将数据3亿用科学记数法表示为（）

A、 $3 \times 10^{5}$ B、 $3 \times 10^{6}$ C、 $3 \times 10^{7}$ D、 $3 \times 10^{8}$

查看试题解析
4. 在平面直角坐标系 $x O y$ 中，点 $M (- 4, 2)$ 关于x轴对称的点的坐标是（）

A、 $(- 4, 2)$ B、 $(4, 2)$ C、 $(- 4, - 2)$ D、 $(4, - 2)$

查看试题解析
5. 下列计算正确的是（）

A、 $3 m n - 2 m n = 1$ B、 ${(m^{2} n^{3})}^{2} = m^{4} n^{6}$ C、 ${(- m)}^{3} \cdot m = m^{4}$ D、 ${(m + n)}^{2} = m^{2} + n^{2}$

查看试题解析
6. 如图，四边形 $A B C D$ 是菱形，点E，F分别在 $B C ， D C$ 边上，添加以下条件不能判定 $△ A B E ≌ △ A D F$ 的是（）

A、 $B E = D F$ B、 $∠ B A E = ∠ D A F$ C、 $A E = A D$ D、 $∠ A E B = ∠ A F D$

查看试题解析
7. 菲尔兹奖是数学领域的一项国际大奖，常被视为数学界的诺贝尔奖，每四年颁发一次，最近一届获奖者获奖时的年龄（单位：岁）分别为：30，40，34，36，则这组数据的中位数是（）

A、34 B、35 C、36 D、40

查看试题解析
8. 分式方程 $\frac{2 - x}{x - 3} + \frac{1}{3 - x} = 1$ 的解为（）

A、 $x = 2$ B、 $x = - 2$ C、 $x = 1$ D、 $x = - 1$

查看试题解析
9. 《九章算术》卷八方程第十题原文为：“今有甲、乙二人持钱不知其数甲得乙半而钱五十，乙得甲太半而亦钱五十.问：甲、乙持钱各几何？”题目大意是：甲、乙两人各带了若干钱.如果甲得到乙所有钱的一半，那么甲共有钱50；如果乙得到甲所有钱的 $\frac{2}{3}$ ，那么乙也共有钱50，问：甲、乙两人各带了多少钱？设甲、乙两人持钱的数量分别为x，y，则可列方程组为（）

A、 ${\begin{array}{l} x + \frac{1}{2} y = 50 \\ y + \frac{2}{3} x = 50 \end{array}$ B、 ${\begin{matrix} x - \frac{1}{2} y = 50 \\ y + \frac{2}{3} x = 50 \end{matrix}$ C、 ${\begin{matrix} 2 x - y = 50 \\ x - \frac{2}{3} x = 50 \end{matrix}$ D、 ${\begin{array}{l} 2 x - y = 50 \\ x - \frac{2}{3} y = 50 \end{array}$

查看试题解析
10. 如图，正六边形 $A B C D E F$ 的边长为6，以顶点A为圆心， $A B$ 的长为半径画圆，则图中阴影部分的面积为（）

A、 $4 π$ B、 $6 π$ C、 $8 π$ D、 $12 π$

查看试题解析

二、填空题

11. 因式分解： $x^{2} - 4 =$ .

查看试题解析
12. 如图，数字代表所在正方形的面积，则A所代表的正方形的面积为.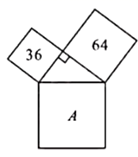

查看试题解析
13. 在平面直角坐标系 $x O y$ 中，若抛物线 $y = x^{2} + 2 x + k$ 与x轴只有一个交点，则 $k =$ .

查看试题解析
14. 如图，在 $R t △ A B C$ 中， $∠ C = 90 ° ， A C = B C$ ，按以下步骤作图：①以点A为圆心，以任意长为半径作弧，分别交 $A C ， A B$ 于点M，N；②分别以M，N为圆心，以大于 $\frac{1}{2} M N$ 的长为半径作弧，两弧在 $∠ B A C$ 内交于点O；③作射线 $A O$ ，交 $B C$ 于点D.若点D到 $A B$ 的距离为1，则 $B C$ 的长为.

查看试题解析
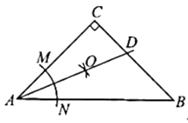15. 在正比例函数 $y = k x$ 中，y的值随着x值的增大而增大，则点 $P (3 ， k)$ 在第象限.

查看试题解析
16. 若m，n是一元二次方程 $x^{2} + 2 x - 1 = 0$ 的两个实数根，则 $m^{2} + 4 m + 2 n$ 的值是.

查看试题解析
17. 如图，在平面直角坐标系 $x O y$ 中，直线 $y = \frac{\sqrt{3}}{3} x + \frac{2 \sqrt{3}}{3}$ 与 $⊙ O$ 相交于A，B两点，且点A在x轴上，则弦 $A B$ 的长为.

查看试题解析
18. 如图，在矩形 $A B C D$ 中， $A B = 4 ， A D = 8$ ，点E，F分别在边 $A D ， B C$ 上，且 $A E = 3$ ，按以下步骤操作：第一步，沿直线 $E F$ 翻折，点A的对应点 $A'$ 恰好落在对角线 $A C$ 上，点B的对应点为 $B'$ ，则线段 $B F$ 的长为；第二步，分别在 $E F ， A^{'} B'$ 上取点M，N，沿直线 $M N$ 继续翻折，使点F与点E重合，则线段 $M N$ 的长为.

查看试题解析
19. 我们对一个三角形的顶点和边都赋给一个特征值，并定义：从任意顶点出发，沿顺时针或逆时针方向依次将顶点和边的特征值相乘，再把三个乘积相加，所得之和称为此三角形的顺序旋转和或逆序旋转和如图1， $a r + c q + b p$ 是该三角形的顺序旋转和， $a p + b q + c r$ 是该三角形的逆序旋转和.已知某三角形的特征值如图2，若从1，2，3中任取一个数作为x，从1，2，3，4中任取一个数作为y，则对任意正整数k，此三角形的顺序旋转和与逆序旋转和的差都小于4的概率是.

查看试题解析

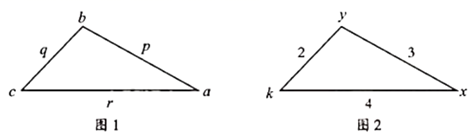
三、解答题

20.

(1)、计算： $\sqrt{4} + {(1 + π)}^{0} - 2 \cos 45 ° + | 1 - \sqrt{2} |$ .

(2)、解不等式组： ${\begin{array}{l} 5 x - 2 > 3 (x + 1) \\ \frac{1}{2} x - 1 \leq 7 - \frac{3}{2} x \end{array}$

查看试题解析
21. 先化简，再求值： $(1 + \frac{2}{a + 1}) \div \frac{a^{2} + 6 a + 9}{a + 1}$ ，其中 $a = \sqrt{3} - 3$ .

查看试题解析
22. 为有效推进儿童青少年近视防控工作，教育部办公厅等十五部门联合制定《儿童青少年近视防控光明行动工作方案（2021－025年）》，共提出八项主要任务，其中第三项任务为强化户外活动和体育锻炼.我市各校积极落实方案精神，某学校决定开设以下四种球类的户外体育选修课程篮球、足球、排球、乒乓球.为了解学生需求，该校随机对本校部分学生进行了“你选择哪种球类课程”的调查（要求必须选择且只能选择其中一门课程），并根据调查结果绘制成如下不完整的统计图表.

课程

人数

篮球

m

足球

21

排球

30

乒乓球

n

根据图表信息，解答下列问题：

(1)、分别求出表中m，n的值；

(2)、求扇形统计图中“足球”对应的扇形圆心角的度数；

(3)、该校共有2000名学生，请你估计其中选择“乒乓球”课程的学生人数.

查看试题解析
23. 越来越多太阳能路灯的使用，既点亮了城市的风景，也是我市积极落实节能环保的举措.某校学生开展综合实践活动，测量太阳能路灯电池板离地面的高度.如图，已知测倾器的高度为1.6米，在测点A处安置测倾器，测得点M的仰角 $∠ M B C = 33 °$ ，在与点A相距3.5米的测点D处安置测倾器，测得点M的仰角 $∠ M E C = 45 °$ （点A，D与N在一条直线上），求电池板离地面的高度 $M N$ 的长.（结果精确到1米；参考数据： $\sin 33 ° \approx 0.54 ， \cos 33 ° \approx 0.84 ， \tan 33 ° \approx 0.65$ ）

查看试题解析
24. 如图，在平面直角坐标系 $x O y$ 中，一次函数 $y = \frac{3}{4} x + \frac{3}{2}$ 的图象与反比例函数 $y = \frac{k}{x} (x > 0)$ 的图象相交于点 $A (a ， 3)$ ，与x轴相交于点B.

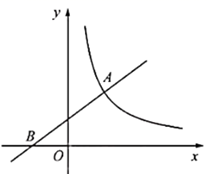(1)、求反比例函数的表达式；

(2)、过点A的直线交反比例函数的图象于另一点C，交x轴正半轴于点D，当 $△ A B D$ 是以 $B D$ 为底的等腰三角形时，求直线 $A D$ 的函数表达式及点C的坐标.

查看试题解析
25. 如图， $A B$ 为 $⊙ O$ 的直径，C为 $⊙ O$ 上一点，连接 $A C ， B C$ ，D为 $A B$ 延长线上一点，连接 $C D$ ，且 $∠ B C D = ∠ A$ .

(1)、求证： $C D$ 是 $⊙ O$ 的切线；

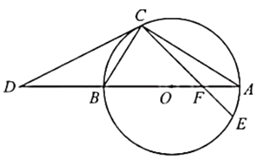(2)、若 $⊙ O$ 的半径为 $\sqrt{5}$ ， $△ A B C$ 的面积为 $2 \sqrt{5}$ ，求 $C D$ 的长；

(3)、在（2）的条件下，E为 $⊙ O$ 上一点，连接 $C E$ 交线段 $O A$ 于点F，若 $\frac{E F}{C F} = \frac{1}{2}$ ，求 $B F$ 的长.

查看试题解析
26. 为改善城市人居环境，《成都市生活垃圾管理条例》（以下简称《条例》）于2021年3月1日起正式施行.某区域原来每天需要处理生活垃圾920吨，刚好被12个A型和10个B型预处置点位进行初筛、压缩等处理.已知一个A型点位比一个B型点位每天多处理7吨生活垃圾.

(1)、求每个B型点位每天处理生活垃圾的吨数；

(2)、由于《条例》的施行，垃圾分类要求提高，现在每个点位每天将少处理8吨生活垃圾，同时由于市民环保意识增强，该区域每天需要处理的生活垃圾比原来少10吨.若该区域计划增设A型、B型点位共5个，试问至少需要增设几个A型点位才能当日处理完所有生活垃圾？

查看试题解析
27. 在 $R t △ A B C$ 中， $∠ A C B = 90 ° ， A B = 5 ， B C = 3$ ，将 $△ A B C$ 绕点B顺时针旋转得到 $△ A^{'} B C^{'}$ ，其中点A，C的对应点分别为点 $A^{'}$ ， $C^{'}$ .

(1)、如图1，当点 $A^{'}$ 落在 $A C$ 的延长线上时，求 $A A^{'}$ 的长；

(2)、如图2，当点 $C^{'}$ 落在 $A B$ 的延长线上时，连接 $C C^{'}$ ，交 $A^{'} B$ 于点M，求 $B M$ 的长；

(3)、如图3，连接 $A A^{'} ， C C^{'}$ ，直线 $C C^{'}$ 交 $A A^{'}$ 于点D，点E为 $A C$ 的中点，连接 $D E$ .在旋转过程中， $D E$ 是否存在最小值？若存在，求出 $D E$ 的最小值；若不存在，请说明理由.

查看试题解析
28. 如图，在平面直角坐标系 $x O y$ 中，抛物线 $y = a {(x - h)}^{2} + k$ 与x轴相交于O，A两点，顶点P的坐标为 $(2 ， - 1)$ .点B为抛物线上一动点，连接 $A P ， A B$ ，过点B的直线与抛物线交于另一点C.

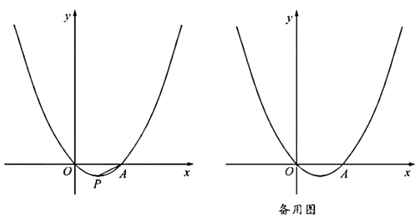(1)、求抛物线的函数表达式；

(2)、若点B的横坐标与纵坐标相等， $∠ A B C = ∠ O A P$ ，且点C位于x轴上方，求点C的坐标；

(3)、若点B的横坐标为t， $∠ A B C = 90 °$ ，请用含t的代数式表示点C的横坐标，并求出当 $t < 0$ 时，点C的横坐标的取值范围.

查看试题解析

课程	人数
篮球	m
足球	21
排球	30
乒乓球	n