浙江省杭州市下城区2021届九年级上学期数学10月月考试卷
试卷更新日期:2021-06-24 类型:月考试卷
一、单选题
-
1. y=x2﹣2x+3的对称轴是直线( )A、x=﹣1 B、x=1 C、y=﹣1 D、y=12. 二次函数y=x(1﹣x)﹣2的一次项系数是( )A、1 B、﹣1 C、2 D、﹣23. 下列事件中,是必然事件的是( )A、从一个只有白球的盒子里摸出一个球是白球 B、任意买一张电影票,座位号是3的倍数 C、掷一枚质地均匀的硬币,正面向上 D、汽车走过一个红绿灯路口时,前方正好是绿灯4. 已知二次函数y=ax2+bx+c(a≠0)的最大值为 ,则( )A、 , B、 , C、 , D、 ,5. 五张完全相同的卡片上,分别画有圆、平行四边形、等边三角形、角、线段,现从中随机抽取一张,恰好抽到轴对称图形的概率是( )A、 B、 C、 D、6. 在同一坐标系中,函数y=ax2+b与y=bx2+ax的图象,只可能是下图中的( )A、
 B、
B、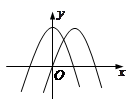 C、
C、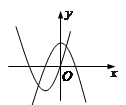 D、
D、 7. 将抛物线C:y=x2+3x-10平移到C′.若两条抛物线C,C′关于直线x=1对称,则下列平移方法中正确的是( )A、将抛物线C向右平移 个单位 B、将抛物线C向右平移3个单位 C、将抛物线C向右平移5个单位 D、将抛物线C向右平移6个单位8. 把一枚六个面编号分别为1,2,3,4,5,6的质地均匀的正方体骰子先后投掷2次,若两个正面朝上的编号分别为m,n,则二次函数 的图象与x轴有两个不同交点的概率是( ).A、 B、 C、 D、9. 二次函数 的图象如图所示,对称轴是直线 .下列结论:① ;② ;③ ;④ ( 为实数).其中结论正确的个数为( )
7. 将抛物线C:y=x2+3x-10平移到C′.若两条抛物线C,C′关于直线x=1对称,则下列平移方法中正确的是( )A、将抛物线C向右平移 个单位 B、将抛物线C向右平移3个单位 C、将抛物线C向右平移5个单位 D、将抛物线C向右平移6个单位8. 把一枚六个面编号分别为1,2,3,4,5,6的质地均匀的正方体骰子先后投掷2次,若两个正面朝上的编号分别为m,n,则二次函数 的图象与x轴有两个不同交点的概率是( ).A、 B、 C、 D、9. 二次函数 的图象如图所示,对称轴是直线 .下列结论:① ;② ;③ ;④ ( 为实数).其中结论正确的个数为( ) A、1个 B、2个 C、3个 D、4个10. 已知二次函数y=﹣(x﹣k+2)(x+k)+m,其中k,m为常数.下列说法正确的是( )A、若k≠1,m≠0,则二次函数y的最大值小于0 B、若k<1,m>0,则二次函数y的最大值大于0 C、若k=1,m≠0,则二次函数y的最大值小于0 D、若k>1,m<0,则二次函数y的最大值大于0
A、1个 B、2个 C、3个 D、4个10. 已知二次函数y=﹣(x﹣k+2)(x+k)+m,其中k,m为常数.下列说法正确的是( )A、若k≠1,m≠0,则二次函数y的最大值小于0 B、若k<1,m>0,则二次函数y的最大值大于0 C、若k=1,m≠0,则二次函数y的最大值小于0 D、若k>1,m<0,则二次函数y的最大值大于0二、填空题
-
11. 把二次函数y=﹣ x2+3x+3化成y=a(x+m)2+k的形式为.12. 同时掷两枚质地均匀的骰子,则至少有一枚骰子的点数是 这个随机事件的概率为 .13. 已知二次函数的图象经过原点及点(﹣3,﹣2),且图象与x轴的另一交点到原点的距离为1,则该二次函数的解析式为.14. 一个不透明的口袋里有10个黑球和若干个黄球,它们除颜色外其余都相同,从口袋中随机摸出一球记下其颜色,再把它放回口袋中摇匀,重复上述过程,共实验200次,其中有120次摸到黄球,由此估计袋中的黄球有个.15. 已知函数y=x2﹣2mx+2015(m为常数)的图象上有三点:A(x1 , y1),B(x2 , y2),C(x3 , y3),其中x1=m﹣ ,x2=m+ ,x3=m﹣1,则y1、y2、y3的大小关系是.16. 对于二次函数y=x2﹣2mx﹣3,下列正确的说法是.
①它的图象与x轴有两个公共点;
②如果当x≤1时,y随x的增大而减小,则m=1;
③如果将它的图象向左平移3个单位后过原点,则m=﹣1;
④如果当x=﹣8时的函数值与x=2020时的函数值相等,则当x=2012时的函数值为﹣3.
三、解答题
-
17. 已知抛物线y=﹣x2+ax+b经过点A(1,0),B(0,﹣4).(1)、求抛物线的解析式;(2)、求此抛物线的顶点坐标.18. 一个不透明的布袋里装有3个白球,1个黑球和若干个红球,它们除颜色外其余都相同,从中任意摸出1个球,是白球的概率 .(1)、布袋里红球有多少个?(2)、先从布袋中摸出1个球后不放回,再摸出1个球,求出两次都摸到白球的概率.19. 甲、乙两个不透明的袋子中,分别装有大小材质完全相同的小球,其中甲口袋中小球编号为1、2、3、4,乙口袋中小球编号分别是2、3、4,先从甲口袋中任意摸出一个小球,记下编号为 ,再从乙袋中摸出一个小球,记下编号为 .(1)、请用画树状图或列表的方法表示 所有可能情况;(2)、规定:若 、 都是方程 的解时,小明获胜;若 、 都不是方程 的解时,小刚获胜,请说明此游戏规则是否公平?20. 在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用28m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=xm.
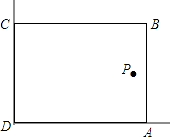 (1)、若花园的面积为192m2 , 求x的值;(2)、若在P处有一棵树与墙CD,AD的距离分别是15m和6m,要将这棵树围在花园内(含边界,不考虑树的粗细),求花园面积S的最大值.21. 新华书店销售一个系列的儿童书刊,每套进价100元,定价为140元,一天可以销售20套.为了扩大销售,增加盈利,减少库存,书店决定采取降价措施.若一套书每降价0.5元,平均每天可多售出1套.设每套书降价x元时,书店一天可获利润y元.(1)、求出y与x的函数关系式;(2)、该书店要获得最大利润,售价应定为每套多少元?(3)、小静说:“当某天的利润最大时,当天的销售额也最大.”你认为对吗?请说明理由.22. 理解发现
(1)、若花园的面积为192m2 , 求x的值;(2)、若在P处有一棵树与墙CD,AD的距离分别是15m和6m,要将这棵树围在花园内(含边界,不考虑树的粗细),求花园面积S的最大值.21. 新华书店销售一个系列的儿童书刊,每套进价100元,定价为140元,一天可以销售20套.为了扩大销售,增加盈利,减少库存,书店决定采取降价措施.若一套书每降价0.5元,平均每天可多售出1套.设每套书降价x元时,书店一天可获利润y元.(1)、求出y与x的函数关系式;(2)、该书店要获得最大利润,售价应定为每套多少元?(3)、小静说:“当某天的利润最大时,当天的销售额也最大.”你认为对吗?请说明理由.22. 理解发现对于三个数a,b,c,用M{a,b,c}表示这三个数的平均数,用min{a,b,c}表示这三个数中最小的数.例如:M{﹣1,2,3}= ;min{﹣1,2,3}=﹣1;min{﹣1,2,a}= ,
解决下列问题:
 (1)、如果min{2,2x+2,4﹣2x}=2,则x的取值范围为≤x≤.(2)、如果M{2,x+1,2x}=min{2,x+1,2x},试求x的值,并请求出从1至9这9个自然数中任取一个,满足x的值的概率.(3)、在同一直角坐标系中作出函数y=x+1,y=(x﹣1)2 , y=2﹣x的图象(不需列表描点).通过观察图象,填空:min{x+1,(x﹣1)2 , 2﹣x}的大值为.23. 如图,在平面直角坐标系中,已知二次函数 图象的顶点为A,与y轴交于点B,异于顶点A的点C(1,n)在该函数图象上.
(1)、如果min{2,2x+2,4﹣2x}=2,则x的取值范围为≤x≤.(2)、如果M{2,x+1,2x}=min{2,x+1,2x},试求x的值,并请求出从1至9这9个自然数中任取一个,满足x的值的概率.(3)、在同一直角坐标系中作出函数y=x+1,y=(x﹣1)2 , y=2﹣x的图象(不需列表描点).通过观察图象,填空:min{x+1,(x﹣1)2 , 2﹣x}的大值为.23. 如图,在平面直角坐标系中,已知二次函数 图象的顶点为A,与y轴交于点B,异于顶点A的点C(1,n)在该函数图象上. (1)、当m=5时,求n的值.(2)、当n=2时,若点A在第一象限内,结合图象,求当y 时,自变量x的取值范围.(3)、作直线AC与y轴相交于点D.当点B在x轴上方,且在线段OD上时,求m的取值范围.
(1)、当m=5时,求n的值.(2)、当n=2时,若点A在第一象限内,结合图象,求当y 时,自变量x的取值范围.(3)、作直线AC与y轴相交于点D.当点B在x轴上方,且在线段OD上时,求m的取值范围.