浙江杭州拱墅区杭州锦绣育才教育集团2020届九年级上学期数学12月月考试卷

试卷更新日期：2021-06-24 类型：月考试卷

进入出卷网下载

一、单选题

1. 由4个小立方体搭成如图所示的几何体，它的左视图是（）

A、 B、 C、 D、

查看试题解析
2. 二次函数y＝x²＋2x－5有

A、最大值－5 B、最小值－5 C、最大值－6 D、最小值－6

查看试题解析
3. 如图所示，四边形ABCD为⊙O的内接四边形，∠BCD=120°，则∠BOD的大小是（）

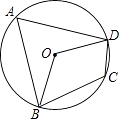A、80° B、120° C、100° D、90°

查看试题解析
4. 在一个不透明的盒子中装有12个白球，若干个黄球，它们除颜色不同外，其余均相同．若从中随机摸出一个球是白球的概率是 $\frac{1}{3}$ ，则黄球的个数为（）

A、18 B、20 C、24 D、28

查看试题解析
5. 已知点 $(- 1 ， y_{1})$ ， $(3 ， y_{2})$ ， $(\frac{1}{2} ， y_{3})$ 在图数 $y = x^{2} + 2 x + 1 + m$ 的图象上，则 $y_{1}$ ， $y_{2}$ ， $y_{3}$ 的大小关系是（）

A、 $y_{1} > y_{2} > y_{3}$ B、 $y_{2} > y_{1} > y_{3}$ C、 $y_{2} > y_{3} > y_{1}$ D、 $y_{3} > y_{1} > y_{2}$

查看试题解析
6. 如图，D、E分别是△ABC的边AB、BC上的点，DE∥AC，若S_△BDE：S_△CDE＝1：3，DC、AE交于点F，则S_△DEF：S_△ACF＝（）

A、 $\frac{1}{3}$ B、 $\frac{1}{4}$ C、 $\frac{1}{9}$ D、 $\frac{1}{16}$

查看试题解析
7. 如图，在正方形网格中，△ABC的位置如图，其中点A、B、C分别在格点上，则sinA的值是（）

A、 $\frac{\sqrt{10}}{10}$ B、 $\frac{1}{3}$ C、 $\frac{\sqrt{5}}{5}$ D、 $\frac{\sqrt{5}}{10}$

查看试题解析
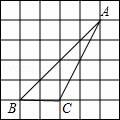8. 一个长方体的三视图如图所示，若其俯视图为正方形，则这个长方体的表面积为（）

A、 $66$ B、 $48$ C、 $48 \sqrt{2} + 36$ D、 $57$

查看试题解析
9. 二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的图象如图所示，则下列说法：① $a b c < 0$ ；② $2 a + b = 0$ ；③ $9 a + 3 b + c > 0$ ；④当 $x < 0$ 时，y随x的增大而减小，其中正确的结论是（）

A、①② B、②③ C、③④ D、②④

查看试题解析
10. 如图，在 $△ A B C$ 中，点D在AB边上， $D E / / B C$ ，与边AC交于点E，连结BE，记 $△ A D E$ ， $△ B C E$ 的面积分别 $S_{1}$ ， $S_{2}$ （）

A、若 $3 A D > A B$ ，则 $5 S_{1} > S_{2}$ B、若 $3 A D > A B$ ，则 $5 S_{1} < S_{2}$ C、若 $3 A D < A B$ ，则 $5 S_{1} > S_{2}$ D、若 $3 A D < A B$ ，则 $5 S_{1} < S_{2}$

查看试题解析

二、填空题

11. 已知圆锥形模具的母线长、半径分别是12cm、4cm，求得这个模具的侧面积是.

查看试题解析
12. 如图，AB是⊙O的直径，∠ACD＝15°，则∠BAD的度数为.

查看试题解析
13. 如图，在正方形网格中，点A、B、C、D都是格点，点E是线段AC上任意一点.如果 $A D = 1$ ，那么当 $A E =$ 时，以点A、D、E为顶点的三角形与 $△ A B C$ 相似.

查看试题解析
14. 已知二次函数 $y = 2 x^{2} - 4 x + 1$ ，当 $0 < x < 4$ 时，y的取值范围是.

查看试题解析
15. 如图，已知花丛中的电线杆AB上有一盏路灯A.灯光下，小明在点C处时，测得他的影长CD＝3米，他沿BC方向行走到点E处时，CE＝2米，测得他的影长EF＝4米，如果小明的身高为1.6米，那么电线杆AB的高度等于米.

查看试题解析
16. 如图，四边形ABCD为正方形. $⊙ O$ 过正方形的顶点A和对角线的交点P，且与AB、AD分别交于点F，E.

(1)、若 $D E = 5$ ，则 $A F =$ .

(2)、若 $A D = 7$ ， $⊙ O$ 的半径为 $\frac{5}{2}$ ，则 $\frac{A E}{D E} =$ .

查看试题解析

三、解答题

17. 计算

(1)、 $\cos^{2} 45 ° + \tan 60 ° \cdot \tan 30 ° + \sin^{2} 45 °$ .

(2)、 $\sqrt{2} \tan 45 ° - \sqrt{3} (\sin 60 ° - 2 \cos 30 °)$ .

查看试题解析
18. 如图， $⊙ O$ 是 $△ A B C$ 的外接圆，AD是 $⊙ O$ 的直径，连结AD，若 $⊙ O$ 的半径 $r = \frac{3}{2}$ ， $A C = 2$ .

(1)、求 $\cos B$ 的值.

(2)、若BC平分 $∠ A C D$ ，求AB的长.

查看试题解析
19. 如图，在 $△ A B C$ 中，AD是角平分线，点E在边AC上，且 $A D^{2} = A E \cdot A B$ ，连接DE.

(1)、求证： $△ A B D ∽ △ A D E$ .

(2)、若 $C D = 3$ ， $C E = \frac{9}{4}$ ，求AC的长.

查看试题解析
20. 如图某幢大楼顶部有广告牌CD．张老师目高MA为1.60米，他站立在离大楼45米的A处测得大楼顶端点D的仰角为30°；接着他向大楼前进14米、站在点B处，测得广告牌顶端点C的仰角为45°．（取 $\sqrt{3} \approx 1.732$ ，计算结果保留一位小数）

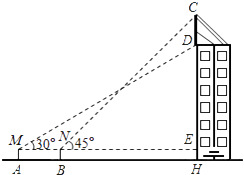(1)、求这幢大楼的高DH；

(2)、求这块广告牌CD的高度．

查看试题解析
21. 如图，已知A、B、C是⊙O上三点，其中 $\overset{⌢}{A B} = 2 \overset{⌢}{B C}$ ，过点B画BD⊥OC于点D.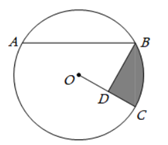

(1)、求证：AB＝2BD；

(2)、若AB＝ $2 \sqrt{3}$ ，CD＝1，求图中阴影部分的面积.

查看试题解析
22. 在平面直角坐标系中，二次函数图象的表达式为 $y = a x^{2} + (a + 1) x$ ，其中 $a \neq 0$ .

(1)、若此函数图象经过点 $(- 2 ， - 6)$ ，求这个二次函数的表达式.

(2)、若 $(x_{1} ， y_{1})$ ， $(x_{2} ， y_{2})$ 为此二次函数图象上两个不同点.
①若 $x_{1} + x_{2} = 4$ ，则 $y_{1} = y_{2}$ ，试求a的值.

②当 $x_{1} > x_{2} \geq 2$ ，对任意的 $x_{1}$ ， $x_{2}$ 都有 $y_{1} < y_{2}$ ，试求a的取值范围.

查看试题解析
23. 如图， $⊙ O$ 经过等边 $△ A B C$ 的顶点A，C（圆心O在 $△ A B C$ 内），分别与AB，CB的延长线交于点D，E，连结DE， $B F ⊥ B C$ 交AE于点F.

(1)、求证： $A D = E C$ .

(2)、当 $A F ： E F = 3 ： 2$ ， $A C = 6$ 时，求 $A E$ 的长.

(3)、设 $\frac{A F}{E F} = x$ ， $\tan ∠ D A E = y$ ，求y关于x的函数表达式.

查看试题解析