四川省绵阳三台县2021届九年级上学期数学12月月考试卷
试卷更新日期:2021-06-24 类型:月考试卷
一、单选题
-
1. 下列标志既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 一元二次方程2x2+x+1=0的根的情况是( )A、有两个相等的实数根 B、有两个不相等的实数根 C、只有一个实数根 D、没有实数根3. 如果关于x的一元二次方程x2+px+q=0的两根分别为x1=3,x2=1,那么这个一元二次方程是( )A、x2+3x+4=0 B、x2﹣4x+3=0 C、x2+4x﹣3=0 D、x2+3x﹣4=04. 一抛物线和抛物线y=-2x2的形状、开口方向完全相同,顶点坐标是(-1,3),则该抛物线的解析式为( )A、y=-2(x-1)2+3 B、y=-2(x+1)2+3 C、y=-(2x+1)2+3 D、y=-(2x-1)2+35. 已知 是关于 的一元二次方程 的两个实数根,是否存在实数 ,使 ,正确的结论是( ).A、 时成立 B、 时成立 C、 或 时成立 D、不存在6. 如图, 是 的直径, 是 的切线, 为切点, 与 交于点 ,连结 .若 ,则 的度数为( )
2. 一元二次方程2x2+x+1=0的根的情况是( )A、有两个相等的实数根 B、有两个不相等的实数根 C、只有一个实数根 D、没有实数根3. 如果关于x的一元二次方程x2+px+q=0的两根分别为x1=3,x2=1,那么这个一元二次方程是( )A、x2+3x+4=0 B、x2﹣4x+3=0 C、x2+4x﹣3=0 D、x2+3x﹣4=04. 一抛物线和抛物线y=-2x2的形状、开口方向完全相同,顶点坐标是(-1,3),则该抛物线的解析式为( )A、y=-2(x-1)2+3 B、y=-2(x+1)2+3 C、y=-(2x+1)2+3 D、y=-(2x-1)2+35. 已知 是关于 的一元二次方程 的两个实数根,是否存在实数 ,使 ,正确的结论是( ).A、 时成立 B、 时成立 C、 或 时成立 D、不存在6. 如图, 是 的直径, 是 的切线, 为切点, 与 交于点 ,连结 .若 ,则 的度数为( ) A、40° B、50° C、60° D、80°7. 如图,AB是⊙O的直径,CD是弦,∠BCD=30°,OA=2,则阴影部分的面积是( )
A、40° B、50° C、60° D、80°7. 如图,AB是⊙O的直径,CD是弦,∠BCD=30°,OA=2,则阴影部分的面积是( )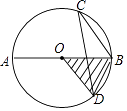 A、 B、 C、π D、2π8. 《九章算术》作为古代中国乃至东方的第一部自成体系的数学专著,与古希腊的《几何原本》并称现代数学的两大源泉.在《九章算术》中记载有一问题“今有圆材埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺,问径几何?”小辉同学根据原文题意,画出圆材截面图如图所示,已知:锯口深为 1寸,锯道AB=1尺(1尺=10寸),则该圆材的直径为( )
A、 B、 C、π D、2π8. 《九章算术》作为古代中国乃至东方的第一部自成体系的数学专著,与古希腊的《几何原本》并称现代数学的两大源泉.在《九章算术》中记载有一问题“今有圆材埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺,问径几何?”小辉同学根据原文题意,画出圆材截面图如图所示,已知:锯口深为 1寸,锯道AB=1尺(1尺=10寸),则该圆材的直径为( )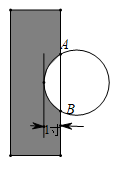 A、13 B、24 C、26 D、289. 如图,正方形 的边长为 ,动点 , 同时从点 出发,在正方形的边上,分别按 , 的方向,都以 的速度运动,到达点 运动终止,连接 ,设运动时间为 , 的面积为 ,则下列图象中能大致表示 与 的函数关系的是( )
A、13 B、24 C、26 D、289. 如图,正方形 的边长为 ,动点 , 同时从点 出发,在正方形的边上,分别按 , 的方向,都以 的速度运动,到达点 运动终止,连接 ,设运动时间为 , 的面积为 ,则下列图象中能大致表示 与 的函数关系的是( )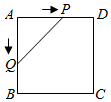 A、
A、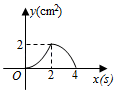 B、
B、 C、
C、 D、
D、 10. 已知:如图,正方形ABCD中,AB=2,AC,BD相交于点O,E,F分别为边BC,CD上的动点(点E,F不与线段BC,CD的端点重合)且BE=CF,连接OE,OF,EF.在点E,F运动的过程中,有下列四个结论:
10. 已知:如图,正方形ABCD中,AB=2,AC,BD相交于点O,E,F分别为边BC,CD上的动点(点E,F不与线段BC,CD的端点重合)且BE=CF,连接OE,OF,EF.在点E,F运动的过程中,有下列四个结论:
①△OEF是等腰直角三角形;
②△OEF面积的最小值是 ;
③至少存在一个△ECF,使得△ECF的周长是 ;
④四边形OECF的面积是1.
所有正确结论的序号是( )
A、①②③ B、③④ C、①②④ D、①②③④11. 不论 取任何实数,抛物线 的顶点都( ).A、在 直线上 B、在直线 上 C、在直线 上 D、不确定12. 若二次函数 的图象与 轴的交点坐标分别是 、 ,且 ,图象上有一点 在 轴下方,对于以下说法:① ;② 是方程 的解;③ ;④ ,对于以上说法正确的是( )A、①②③④ B、①②④ C、③④ D、①③二、填空题
-
13. 如图,在 中, ,将 绕着点 顺时针旋转后,得到 ,且点 在 上,则 的度数为.
 14. 成都轨道交通2号线地质条件最为复杂、盾构施工难度最大的宝长区间顺利贯通.至此,2号线全部38个单线盾构区间全部贯通.当两名乘客通过此地铁闸口时,两名乘客选择不同闸口通过的概率是.
14. 成都轨道交通2号线地质条件最为复杂、盾构施工难度最大的宝长区间顺利贯通.至此,2号线全部38个单线盾构区间全部贯通.当两名乘客通过此地铁闸口时,两名乘客选择不同闸口通过的概率是. 15. 已知 是方程 的两个实数根,则 .16. 若关于 的方程 的解为 ,则方程 的解为.17. 如图,已知 中, 为直径, 平分 ,弦 ,则 半径的为 .
15. 已知 是方程 的两个实数根,则 .16. 若关于 的方程 的解为 ,则方程 的解为.17. 如图,已知 中, 为直径, 平分 ,弦 ,则 半径的为 . 18. 如图,已知直线 与抛物线 与 轴交于点 (点 在点 左侧),与 轴交于点 .点 是 轴上一动点,点 为直线 上一点,则 的最小值为.
18. 如图,已知直线 与抛物线 与 轴交于点 (点 在点 左侧),与 轴交于点 .点 是 轴上一动点,点 为直线 上一点,则 的最小值为.
三、解答题
-
19. 解答下列各题.(1)、解下列方程: .(2)、先化简,再求值: ,其中 满足方程: .20. 李老师为了了解班级学生自主学习、合作交流的具体情况,对九(1)班部分学生进行了为期半个月的跟踪调查,并将调查结果分成四类,A:特别好;B:好;C;一般;D:较差,并将调查结果绘制成以下两幅不完整的统计图.请你根据统计图解答下列问题:
 (1)、本次调查中,李老师一共调查了名同学,其中女生共有名.(2)、将上面的条形统计图补充完整;(3)、为了共同进步,李老师想从被调查的A类和D类学生中分别选取一位同学进行“一帮一”互助学习,请求所选两位同学恰好是一位男同学和一位女同学的概率.21. 在平面直角坐标系中,△ABC的顶点坐标分别是A(2,4)、B(1,2)、C(5,3),如图:
(1)、本次调查中,李老师一共调查了名同学,其中女生共有名.(2)、将上面的条形统计图补充完整;(3)、为了共同进步,李老师想从被调查的A类和D类学生中分别选取一位同学进行“一帮一”互助学习,请求所选两位同学恰好是一位男同学和一位女同学的概率.21. 在平面直角坐标系中,△ABC的顶点坐标分别是A(2,4)、B(1,2)、C(5,3),如图: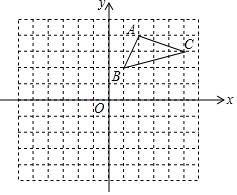
(1)以点(0,0)为旋转中心,将△ABC顺时针转动90°,得到△A1B1C1 , 在坐标系中画出△A1B1C1 , 写出A1、B1、C1的坐标;
(2)在(1)中,若△ABC上有一点P(m,n),直接写出对应点P1的坐标.
(3)作出△ABC关于点O的中心对称图形△A2B2C2.22. 某工厂计划在每个生产周期内生产并销售完某型设备,设备的生产成本为10万元/件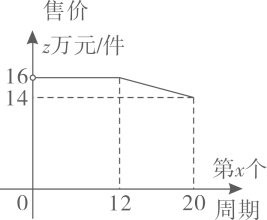 (1)、如图,设第x(0<x≤20)个生产周期设备售价z万元/件,z与x之间的关系用图中的函数图象表示,求z关于x的函数解析式(写出x的范围).(2)、设第x个生产周期生产并销售的设备为y件,y与x满足关系式y=5x+40(0<x≤20).在(1)的条件下,工厂在第几个生产周期创造的利润最大?最大为多少万元?(利润=收入-成本)23. 如图,在 中, .(1)、如图1,若 为 的中点,以 为圆心, 为半径作 交 于点 ,过 作 ,垂足为 .
(1)、如图,设第x(0<x≤20)个生产周期设备售价z万元/件,z与x之间的关系用图中的函数图象表示,求z关于x的函数解析式(写出x的范围).(2)、设第x个生产周期生产并销售的设备为y件,y与x满足关系式y=5x+40(0<x≤20).在(1)的条件下,工厂在第几个生产周期创造的利润最大?最大为多少万元?(利润=收入-成本)23. 如图,在 中, .(1)、如图1,若 为 的中点,以 为圆心, 为半径作 交 于点 ,过 作 ,垂足为 .
①试说明: .
②判断直线 与 的位置关系,并说明理由.
(2)、如图2,若点 沿 向点 移动,以 为圆心,以 为半径作 与 相切于点 ,与 相交于点 ,与 相交于点 ,垂足为 ,已知 的半径长为4, ,求切线 的长. 24. 如图1,已知抛物线 与 轴交于 、 两点, 点在 点的左侧,点 在 轴的负半轴上, ,点 为抛物线顶点,抛物线的对称轴 交 轴于点 ,连接 .过点 的直线 与 轴、 、抛物线分别交于点 , .
24. 如图1,已知抛物线 与 轴交于 、 两点, 点在 点的左侧,点 在 轴的负半轴上, ,点 为抛物线顶点,抛物线的对称轴 交 轴于点 ,连接 .过点 的直线 与 轴、 、抛物线分别交于点 , . (1)、求抛物线的解析式.(2)、 , 点 的坐标为.(3)、如图2,连接 .
(1)、求抛物线的解析式.(2)、 , 点 的坐标为.(3)、如图2,连接 .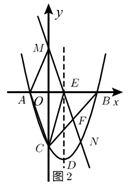
①证明:四边形 为菱形.
② .
(4)、平面内存在的点 使以 为顶点的四边形是平行四边形,请直接写出点 坐标.25. 如图,在平面直角坐标系中,点 的坐标是 与 轴相切于点 ,与 轴相交于 两点.
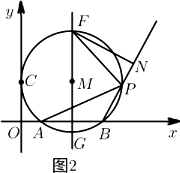 (1)、分别求 三点的坐标.(2)、如图1,设经过 两点的抛物线解析式为 ,它的顶点为 ,求证:直线 与 相切.(3)、如图2,过点 作直线 轴,与圆分别交于 两点,点 为 上任意一点(不与 重合),连接 的延长线于点 .请问 是否为定值,若为定值,请求出这个值,若不为定值,请说明理由.
(1)、分别求 三点的坐标.(2)、如图1,设经过 两点的抛物线解析式为 ,它的顶点为 ,求证:直线 与 相切.(3)、如图2,过点 作直线 轴,与圆分别交于 两点,点 为 上任意一点(不与 重合),连接 的延长线于点 .请问 是否为定值,若为定值,请求出这个值,若不为定值,请说明理由.