四川省泸州市合江县第六片区2021届九年级上学期数学第二次月考试卷
试卷更新日期:2021-06-24 类型:月考试卷
一、单选题
-
1. 下列安全标志图中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列事件中是必然发生的事件是( )A、抛两枚均匀的硬币,硬币落地后,都是正面朝上 B、射击运动员射击一次,命中十环 C、在地球上,抛出的篮球会下落 D、明天会下雨3. 对于二次函数y=(x-1)2+2的图象,下列说法正确的是( )A、开口向下 B、对称轴是x=-1 C、顶点坐标是(1,2) D、与x轴有两个交点4. 方程x2-3x-5=0的根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法确定是否有实数根5. 已知点A 与点B 关于 轴对称,则 的值为( )A、 B、 C、 D、6. 如图,AB是⊙O的直径,弦CD⊥AB于点E.若AB=8,AE=1,则弦CD的长是( )
2. 下列事件中是必然发生的事件是( )A、抛两枚均匀的硬币,硬币落地后,都是正面朝上 B、射击运动员射击一次,命中十环 C、在地球上,抛出的篮球会下落 D、明天会下雨3. 对于二次函数y=(x-1)2+2的图象,下列说法正确的是( )A、开口向下 B、对称轴是x=-1 C、顶点坐标是(1,2) D、与x轴有两个交点4. 方程x2-3x-5=0的根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法确定是否有实数根5. 已知点A 与点B 关于 轴对称,则 的值为( )A、 B、 C、 D、6. 如图,AB是⊙O的直径,弦CD⊥AB于点E.若AB=8,AE=1,则弦CD的长是( )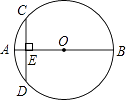 A、 B、2 C、6 D、87. 已知⊙O的直径为16cm,圆心到直线L的距离为6cm,则直线L与⊙O的公共点个数为( )A、2 B、1 C、0 D、不确定8. 若正三角形的外接圆半径长为4,则它的边长为( )A、4 B、 C、2 D、9. 在平面直角坐标系中,平移二次函数y=x2+4x+3的图象能够与二次函数y=x2的图象重合,则平移方式为( )A、向左平移2个单位,向下平移1个单位 B、向左平移2个单位,向上平移1个单位 C、向右平移2个单位,向下平移1个单位 D、向右平移2个单位,向上平移1个单位10. 已知m,n是关于x的一元二次方程x2﹣2tx+t2﹣2t+4=0的两实数根,则(m+2)(n+2)的最小值是( )
A、 B、2 C、6 D、87. 已知⊙O的直径为16cm,圆心到直线L的距离为6cm,则直线L与⊙O的公共点个数为( )A、2 B、1 C、0 D、不确定8. 若正三角形的外接圆半径长为4,则它的边长为( )A、4 B、 C、2 D、9. 在平面直角坐标系中,平移二次函数y=x2+4x+3的图象能够与二次函数y=x2的图象重合,则平移方式为( )A、向左平移2个单位,向下平移1个单位 B、向左平移2个单位,向上平移1个单位 C、向右平移2个单位,向下平移1个单位 D、向右平移2个单位,向上平移1个单位10. 已知m,n是关于x的一元二次方程x2﹣2tx+t2﹣2t+4=0的两实数根,则(m+2)(n+2)的最小值是( )
A、7 B、11 C、12 D、1611. 在同一坐标系中,一次函数 与二次函数 的图象可能是( ).A、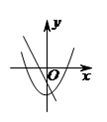 B、
B、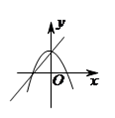 C、
C、 D、
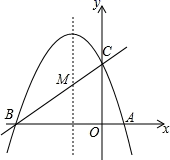
D、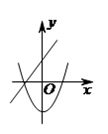 12. 已知抛物线y= x2+1具有如下性质:该抛物线上任意一点到定点F(0,2)的距离与到x轴的距离始终相等,如图,点M的坐标为( ,3),P是抛物线y= x2+1上一个动点,则△PMF周长的最小值是( )
12. 已知抛物线y= x2+1具有如下性质:该抛物线上任意一点到定点F(0,2)的距离与到x轴的距离始终相等,如图,点M的坐标为( ,3),P是抛物线y= x2+1上一个动点,则△PMF周长的最小值是( )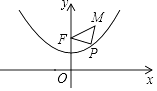 A、3 B、4 C、5 D、6
A、3 B、4 C、5 D、6二、填空题
-
13. 已知P(x,y)在第三象限,且|x|=1,|y|=7,则点P关于原点对称的点的坐标是.14. 在一个不透明的袋子中装有4个红球和2个白球,这些球除了颜色外无其他差别,从袋子中随机摸出一个球,则摸出白球的概率是 .15. 已知圆柱体的底面半径为3cm,高为4cm,则圆柱体的侧面积为。16. 在△ABC中,已知BD和CE分别是边AC、AB上的中线,且BD⊥CE,垂足为O.若OD=2cm,OE=4cm,则线段AO的长度为 cm.
三、解答题
-
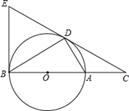
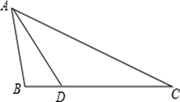
17. 计算:18. 已知:如图,△ABC中,AB =4,BC =8,D为BC边上一点,BD =2.求证:∠BDA =∠BAC.
 19. 解方程: .20. 为了解某中学学生课余生活情况,对喜爱看课外书、体育活动、看电视、社会实践四个方面的人数进行调查统计.现从该校随机抽取 名学生作为样本,采用问卷调查的方法收集数据(参与问卷调查的每名学生只能选择其中一项).并根据调查得到的数据绘制成了如图所示的两幅不完整的统计图.由图中提供的信息,解答下列问题:
19. 解方程: .20. 为了解某中学学生课余生活情况,对喜爱看课外书、体育活动、看电视、社会实践四个方面的人数进行调查统计.现从该校随机抽取 名学生作为样本,采用问卷调查的方法收集数据(参与问卷调查的每名学生只能选择其中一项).并根据调查得到的数据绘制成了如图所示的两幅不完整的统计图.由图中提供的信息,解答下列问题: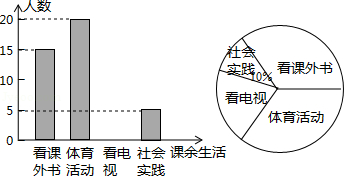 (1)、求n的值;(2)、若该校学生共有1200人,试估计该校喜爱看电视的学生人数;(3)、若调查到喜爱体育活动的4名学生中有3名男生和1名女生,现从这4名学生中任意抽取2名学生,求恰好抽到2名男生的概率.21. 某水果批发商场经销一种高档水果,如果每千克盈利10元,每天可售出500千克.经市场调查发现,在进货价不变的情况下,若每千克涨价1元,日销售量将减少20千克.(1)、现该商场要保证每天盈利6 000元,同时又要顾客得到实惠,那么每千克应涨价多少元?(2)、若该商场单纯从经济角度看,每千克这种水果涨价多少元,能使商场获利最多?22. 关于 的一元二次方程 有两个不等实根 , .(1)、求实数 的取值范围;(2)、若方程两实根 , 满足 ,求 的值。23. 如图,在平面直角坐标系 中,已知一次函数 的图象与反比例函数 的图象相交于A , B两点.且点A的坐标为 .
(1)、求n的值;(2)、若该校学生共有1200人,试估计该校喜爱看电视的学生人数;(3)、若调查到喜爱体育活动的4名学生中有3名男生和1名女生,现从这4名学生中任意抽取2名学生,求恰好抽到2名男生的概率.21. 某水果批发商场经销一种高档水果,如果每千克盈利10元,每天可售出500千克.经市场调查发现,在进货价不变的情况下,若每千克涨价1元,日销售量将减少20千克.(1)、现该商场要保证每天盈利6 000元,同时又要顾客得到实惠,那么每千克应涨价多少元?(2)、若该商场单纯从经济角度看,每千克这种水果涨价多少元,能使商场获利最多?22. 关于 的一元二次方程 有两个不等实根 , .(1)、求实数 的取值范围;(2)、若方程两实根 , 满足 ,求 的值。23. 如图,在平面直角坐标系 中,已知一次函数 的图象与反比例函数 的图象相交于A , B两点.且点A的坐标为 .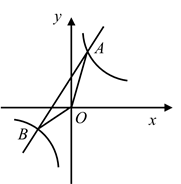 (1)、求该一次函数的解析式;(2)、求 的面积.
(1)、求该一次函数的解析式;(2)、求 的面积.