广西北部湾经济区2021届九年级上学期数学第二次月考试卷
试卷更新日期:2021-06-24 类型:月考试卷
一、单选题
-
1. 在下列四个图案中,不是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 如图,在 中,∠C=90°,设∠A , ∠B , ∠C所对的边分别为a , b , c , 则( )
2. 如图,在 中,∠C=90°,设∠A , ∠B , ∠C所对的边分别为a , b , c , 则( ) A、c=bsinB B、b=csinB C、a=btanB D、b=ctanB3. 如图,直线 与,直线 分别交 , , 于点 , , ;直线 分别交 , , 于点 , , , 与 相交于点 ,且 , , ,则 的值为( )
A、c=bsinB B、b=csinB C、a=btanB D、b=ctanB3. 如图,直线 与,直线 分别交 , , 于点 , , ;直线 分别交 , , 于点 , , , 与 相交于点 ,且 , , ,则 的值为( ) A、 B、 C、 D、4. 如图,在直角坐标系中,有两点A(6,3)、B(6,0).以原点O为位似中心,相似比为 ,在第一象限内把线段AB缩小后得到线段CD,则点C的坐标为( )
A、 B、 C、 D、4. 如图,在直角坐标系中,有两点A(6,3)、B(6,0).以原点O为位似中心,相似比为 ,在第一象限内把线段AB缩小后得到线段CD,则点C的坐标为( )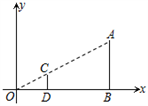 A、(2,1) B、(2,0) C、(3,3) D、(3,1)5. 把抛物线 平移得到抛物线 ,是怎样平移得到的( )A、向右平移2个单位长度,再向上平移4个单位长度 B、向左平移2个单位长度,再向下平移4个单位长度 C、向右平移4个单位长度,再向上平移2个单位长度 D、向左平移4个单位长度,再向下平移2个单位长度6. 中, 、 都是锐角,且 , ,则 的形状是( ).A、直角三角形 B、钝角三角形 C、锐角三角形 D、不能确定7. 函数 与 在同一直角坐标系中的图象可能是( )A、
A、(2,1) B、(2,0) C、(3,3) D、(3,1)5. 把抛物线 平移得到抛物线 ,是怎样平移得到的( )A、向右平移2个单位长度,再向上平移4个单位长度 B、向左平移2个单位长度,再向下平移4个单位长度 C、向右平移4个单位长度,再向上平移2个单位长度 D、向左平移4个单位长度,再向下平移2个单位长度6. 中, 、 都是锐角,且 , ,则 的形状是( ).A、直角三角形 B、钝角三角形 C、锐角三角形 D、不能确定7. 函数 与 在同一直角坐标系中的图象可能是( )A、 B、
B、 C、
C、 D、
D、 8. 如图,在平面直角坐标系中,一次函数 的图象与 轴、 轴分别相交于点 ,点 ,以线段 为边作正方形 ,且点 在反比例函数 的图象上,则 的值为( )
8. 如图,在平面直角坐标系中,一次函数 的图象与 轴、 轴分别相交于点 ,点 ,以线段 为边作正方形 ,且点 在反比例函数 的图象上,则 的值为( ) A、 B、 C、 D、209. 如图,PA、PB为圆O的切线,切点分别为A、B,PO交AB于点C,PO的延长线交圆O于点D,下列结论不一定成立的是( )
A、 B、 C、 D、209. 如图,PA、PB为圆O的切线,切点分别为A、B,PO交AB于点C,PO的延长线交圆O于点D,下列结论不一定成立的是( ) A、PA=PB B、∠BPD=∠APD C、AB⊥PD D、AB平分PD10. 下列命题:①两个相似多边形面积之比等于相似比的平方:②两个相似三角形的对应高之比等于它们的相似比;③在 与 中, , ,那么 ;④已知 及位似中心O,能够作一个且只能作一个三角形与 位似,使位似比为2其中真命题的个数是( )A、1个 B、2个 C、3个 D、4个11. 如图,在矩形 中, , ,以点 为圆心, 长为半径画弧交边 于点 ,连接 ,则 的长为( )
A、PA=PB B、∠BPD=∠APD C、AB⊥PD D、AB平分PD10. 下列命题:①两个相似多边形面积之比等于相似比的平方:②两个相似三角形的对应高之比等于它们的相似比;③在 与 中, , ,那么 ;④已知 及位似中心O,能够作一个且只能作一个三角形与 位似,使位似比为2其中真命题的个数是( )A、1个 B、2个 C、3个 D、4个11. 如图,在矩形 中, , ,以点 为圆心, 长为半径画弧交边 于点 ,连接 ,则 的长为( )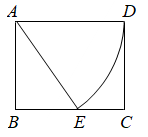 A、 B、 C、 D、12. 如图,平面直角坐标系中,分别以点 , 为圆心,以1、2为半径作 , , , 分别是 , 上的动点, 为 轴上的动点,则 的最小值等于( )
A、 B、 C、 D、12. 如图,平面直角坐标系中,分别以点 , 为圆心,以1、2为半径作 , , , 分别是 , 上的动点, 为 轴上的动点,则 的最小值等于( )
 A、5 B、10 C、 D、
A、5 B、10 C、 D、二、填空题
-
13. 在平面直角坐标系中,点 关于原点对称的点的坐标是.14. 如图, , ,则图中相似三角形有对.
 15. 如图,在高2米,坡角为30°的楼梯表面铺地毯,地毯的长至少需米.
15. 如图,在高2米,坡角为30°的楼梯表面铺地毯,地毯的长至少需米.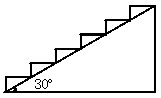 16. 如图,在 中, , , 为 边上的一点,且 .若 的面积为1,则 的面积为.
16. 如图,在 中, , , 为 边上的一点,且 .若 的面积为1,则 的面积为.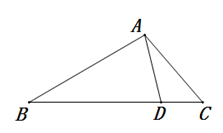 17. 如图,在 中, , , ,以点 为圆心 为半径作圆,如果 与 有唯一公共点,则半径 的值是.
17. 如图,在 中, , , ,以点 为圆心 为半径作圆,如果 与 有唯一公共点,则半径 的值是.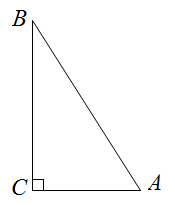 18. 如图,已知:函数 与函数 ,则函数 的最小值是.
18. 如图,已知:函数 与函数 ,则函数 的最小值是.
三、解答题
-
19. 计算: .20. 如图,在 中, ,在 边上取一点 ,使 ,过 作 交 于 , .求 的长.
 21. 如图,在平面直角坐标系中,一次函数 的图象与反比例函数 的图象交于A、B两点,已知 , .
21. 如图,在平面直角坐标系中,一次函数 的图象与反比例函数 的图象交于A、B两点,已知 , .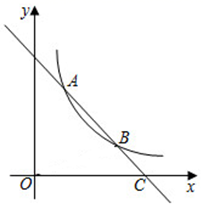 (1)、求反比例函数的表达式;(2)、当 时,求不等式 的解集.22. 如图,已知 为 的直径, 是弦,且 于点 .连接 , , .
(1)、求反比例函数的表达式;(2)、当 时,求不等式 的解集.22. 如图,已知 为 的直径, 是弦,且 于点 .连接 , , . (1)、求证: ;(2)、若 , ,求 的直径.23. 九年级数学兴趣小组去测量一座小山的高度,在小山顶上有一高度为20米的发射塔AB,如图所示.在山脚平地上的D处测得塔底B的仰角为 ,向小山前进100米到达点E处,测得塔顶A的仰角为 ,求小山BC的高度.(结果保留根号)
(1)、求证: ;(2)、若 , ,求 的直径.23. 九年级数学兴趣小组去测量一座小山的高度,在小山顶上有一高度为20米的发射塔AB,如图所示.在山脚平地上的D处测得塔底B的仰角为 ,向小山前进100米到达点E处,测得塔顶A的仰角为 ,求小山BC的高度.(结果保留根号)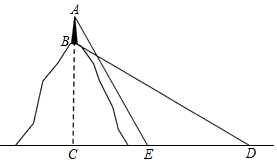 24. 如图,在平行四边形 中, 为对角线 上一点, 交 于点 ,交 的延长线于点 .
24. 如图,在平行四边形 中, 为对角线 上一点, 交 于点 ,交 的延长线于点 . (1)、请找出一对相似的三角形并证明;(2)、若 ,求 的值.
(1)、请找出一对相似的三角形并证明;(2)、若 ,求 的值.

