浙江省瑞安市六校联盟2020-2021学年八年级上学期数学学业检测试卷

试卷更新日期：2021-06-24 类型：开学考试

进入出卷网下载

一、单选题

1. 数1，0， $- \frac{2}{3}$ ，﹣2中最大的是（）

A、1 B、0 C、 $- \frac{2}{3}$ D、﹣2

查看试题解析
2. 下面四个图形中，∠1与∠2是对顶角的图形（）

A、 B、 C、 D、

查看试题解析
3. 下列方程组中是二元一次方程组的是（）

A、 ${\begin{array}{l} \frac{2}{x} - y = 4 \\ 2 x + y = 1 \end{array}$ B、 ${\begin{array}{l} x - y = 4 \\ 2 x + y = 3 \end{array}$ C、 ${\begin{array}{l} 2 x - y = 5 \\ 2 y + z = 1 \end{array}$ D、 ${\begin{array}{l} x + y = 5 \\ x^{2} + y^{2} = 12 \end{array}$

查看试题解析
4. 下列计算正确的是（）

A、 $a^{2} \cdot a^{4} = a^{6}$ B、 ${(x - 1)}^{2} = x^{2} - 1$ C、 $3 a^{2} b - 3 a b^{2} = 0$ D、 ${(a^{2})}^{5} = a^{7}$

查看试题解析
5. 下列调查方式中，你认为最合适的是（）

A、肺炎疫情期间，对学生体温测量采用抽样调查 B、驰援武汉医疗队胜利归来时，为了确定医疗队成员的健康情况，可采用抽样调查 C、检查一批口罩的防护效果时，采用全面调查 D、肺炎疫情期间到校上课，了解学生健康码情况时，采用全面调查

查看试题解析
6. 已知直线 $m / / n$ ，将一块含 $30 °$ 角的直角三角板 $A B C$ 按如图方式放置（ $∠ A B C = 30 °$ ），其中 $A$ ， $B$ 两点分别落在直线 $m$ ， $n$ 上，若 $∠ 1 = 40 °$ ，则 $∠ 2$ 的度数为（）

A、 $10 °$ B、 $20 °$ C、 $30 °$ D、 $40 °$

查看试题解析
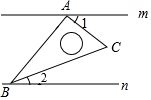7. 若多项式 $x^{2} + m x - 8$ 因式分解的结果为 $(x + 4) (x - 2)$ ，则常数m的值为（）

A、 $- 2$ B、2 C、 $- 6$ D、6

查看试题解析
8. 若 $a^{2} = 16$ ， $b^{2} = 25$ ，且 $a b < 0$ ，则 $a - b$ 的值为（）

A、 $- 9$ B、 $- 1$ C、 $\pm 9$ D、 $\pm 1$

查看试题解析
9. 抗击新冠肺炎疫情期间，某口罩厂接到加大生产的紧急任务后积极扩大产能，现在每天生产的口罩比原来多4万个.已知现在生产100万个口罩所需的时间与原来生产60万个口罩所需的时间相同，问口罩厂现在每天生产多少个口罩？设原来每天生产 $x$ 万个口罩，则由题意可列出方程 $($ $)$

A、 $\frac{100}{x - 4} = \frac{60}{x}$ B、 $\frac{100}{x + 4} = \frac{60}{x}$ C、 $\frac{60}{x - 4} = \frac{100}{x}$ D、 $\frac{60}{x + 4} = \frac{100}{x}$

查看试题解析
10. 如图，将几个小正方形与小长方形拼成一个边长为 $(a + b + c)$ 的正方形.用不同的方法计算这个边长为 $(a + b + c)$ 的正方形面积，就可以得到一个等式 ${(a + b + c)}^{2} = a^{2} + b^{2} + c^{2} + 2 a b + 2 a c + 2 b c$ ，若三个实数x，y，z满足 $2^{x} \times 4^{y} \div 8^{z} = \frac{1}{4}$ ， $x^{2} + 4 y^{2} + 9 z^{2} = 44$ ，利用等式求得 $2 x y - 3 x z - 6 y z$ 的值为（）

A、 $- 20$ B、 $- 40$ C、 $24$ D、 $48$

查看试题解析

二、填空题

11. 数据 $1700000$ 用科学记数法表示为.

查看试题解析
12. 要使分式 $\frac{1 - x}{x - 2}$ 的值为0，则x的值为.

查看试题解析
13. 如图，数轴上点A表示的无理数可能是.

查看试题解析
14. 若一个角的补角是这个角的余角的4倍，则这个角的度数为.

查看试题解析
15. 若 ${\begin{array}{l} x = a \\ y = b \end{array}$ 是方程组 ${\begin{array}{l} 2 x + 3 y = - 5 \\ 2 x - 3 y = 7 \end{array}$ 的解，则代数式 $9 b^{2} - 4 a^{2}$ 的值是.

查看试题解析
16. 如图， $Δ A B C$ 中， $∠ B = 90 °$ ， $∠ A = 30 °$ ，E，F分别是边 $A B$ ， $A C$ 上的点，连结 $E F$ ，将 $Δ A E F$ 沿着者 $E F$ 折叠，得到 $Δ A^{'} E F$ ，当 $Δ A^{'} E F$ 的边 $A^{'} F$ 与 $Δ A B C$ 的三边有一组边平行时， $∠ A E F$ 的度数是.

查看试题解析

三、解答题

17.

(1)、计算： $\sqrt{4} - | - 2 | + {(\sqrt{6})}^{0} - (- 1)$ ；

(2)、化简： ${(x - 1)}^{2} - x (x + 7)$ .

查看试题解析
18. 解下列方程（组）

(1)、 ${\begin{array}{l} x - y = 8 \\ 3 x + y = 12 \end{array}$

(2)、 $\frac{2 x - 1}{x - 3} = 1$

查看试题解析
19. 先化简，再求值： $(x^{2} - y^{2}) \div \frac{x - y}{x y}$ ，其中 $x = 1$ ， $y = - 2$

查看试题解析

20. 某市在开展线上教学活动期间，为更好地组织初中学生居家体育锻炼，随机抽取了部分初中学生对“最喜爱的体育锻炼项目”进行线上问卷调查（每人必须且只选其中一项），得到如下两幅不完整的统计图表，请根据图表信息回答下列问题：

类别	项目	人数
A	跳绳	59
B	健身操	▲
C	俯卧撑	31
D	开合跳	▲
E	其它	22

(1)、求参与问卷调查的学生总人数.

(2)、在参与问卷调查的学生中，最喜爱“开合跳”的学生有多少人？

(3)、该市共有初中学生约8000人，估算该市初中学生中最喜爱“健身操”的人数.

查看试题解析

21. 如图， $∠ A + ∠ A B C = 180 °$ ， $B D ⊥ C D$ 于点D， $E F ⊥ C D$ 于点F.

(1)、请说明 $A D / / B C$ 的理由；

(2)、若 $∠ A D B = 45 °$ ，求 $∠ F E C$ 的度数.

查看试题解析
22. 如图1是小温设计的班徽，其中“ $Z$ ”字型部分按以下作图方式得到：如图2，在正方形 $A B C D$ 边 $A B$ ， $C D$ 上分别取点E，F，再在 $C B$ 和 $A D$ 的延长线上分别取点G，H，使得 $B E = B G = D F = D H$ ，连结 $A G$ ， $E G$ ， $A F$ ， $C E$ ， $F H$ 和 $C H$ .记 $Δ A E G$ 与 $Δ C F H$ 的面积之和为 $S_{1}$ ，四边形 $A E C F$ 的积为 $S_{2}$ ，设 $B E = x$ ， $A E = y$ .
　

(1)、求 $S_{1} =$ ， $S_{2} =$ （用含x、y的代数式表示）

(2)、若 $\frac{S_{1}}{S_{2}} = \frac{2}{5}$ ， $S_{1} + S_{2} = 21$ ，求正方形 $A B C D$ 的面积.

查看试题解析
23. 目前，新型冠状病毒在我国虽可控可防，但不可松懈.某校欲购置规格分别为 $300 m l$ 和 $500 m l$ 的甲、乙两种免洗手消毒液若干瓶，已知购买2瓶甲和1瓶乙免洗手消毒液需要 $55$ 元，购买 $3$ 瓶甲和 $4$ 瓶乙免洗手消毒液需要 $145$ 元.

(1)、求甲、乙两种免洗手消毒液的单价.

(2)、为节约成本，该校购买散装免洗手消毒液进行分装，现需将 $9.6 L$ 的免洗手消毒液全部装入最大容量分别为 $300 m l$ 和 $500 m l$ 的两种空瓶中（每瓶均装满），若分装时平均每瓶需损耗 $20 m l$ ，请问如何分装能使总损耗最小，求出此时需要的两种空瓶的数量.

查看试题解析