福建省福州市闽侯县2021届九年级上学期数学开学试卷
试卷更新日期:2021-06-24 类型:开学考试
一、单选题
-
1. 直角三角形两条直角边的长分别为6和8,则斜边长为( )A、8 B、9 C、10 D、122. 如图,在矩形 中,对角线 , 相交于点O.下列结论中不一定成立的是( )
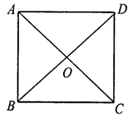 A、 B、 ∥ C、 D、3. 若 是关于x的一次函数,则m的值为( )A、2 B、-2 C、 D、4. 11位参加晋级比赛的选手的成绩各不相同,按成绩取前6名进入决赛如果小明知道了自己的成绩后,要判断自己是否进入决赛,小明只需要知道这11名选手成绩的( )A、 平均数 B、众数 C、中位数 D、方差5. 我国是最早了解勾股定理的国家之一.下面四幅图中,不能用来证明勾股定理的是( )A、
A、 B、 ∥ C、 D、3. 若 是关于x的一次函数,则m的值为( )A、2 B、-2 C、 D、4. 11位参加晋级比赛的选手的成绩各不相同,按成绩取前6名进入决赛如果小明知道了自己的成绩后,要判断自己是否进入决赛,小明只需要知道这11名选手成绩的( )A、 平均数 B、众数 C、中位数 D、方差5. 我国是最早了解勾股定理的国家之一.下面四幅图中,不能用来证明勾股定理的是( )A、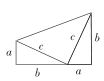 B、
B、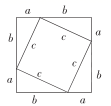 C、
C、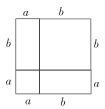 D、
D、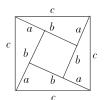 6. 如图,一根竹竿AB,斜靠在竖直的墙上,P是AB中点,A′B′表示竹竿AB端沿墙上、下滑动过程中的某个位置,则在竹竿AB滑动过程中OP( )
6. 如图,一根竹竿AB,斜靠在竖直的墙上,P是AB中点,A′B′表示竹竿AB端沿墙上、下滑动过程中的某个位置,则在竹竿AB滑动过程中OP( )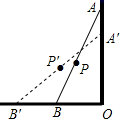 A、下滑时,OP增大 B、上升时,OP减小 C、无论怎样滑动,OP不变 D、只要滑动,OP就变化7. 如图,平行四边形 的对角线 与 相交于点O, 于点E, , , ,则 的长为( )
A、下滑时,OP增大 B、上升时,OP减小 C、无论怎样滑动,OP不变 D、只要滑动,OP就变化7. 如图,平行四边形 的对角线 与 相交于点O, 于点E, , , ,则 的长为( )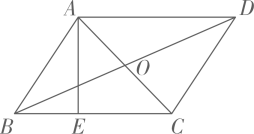 A、 B、 C、 D、8. 已知一次函数 和 ,函数 和 的图象可能是( )A、
A、 B、 C、 D、8. 已知一次函数 和 ,函数 和 的图象可能是( )A、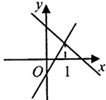 B、
B、 C、
C、 D、
D、 9. 如图,点 ,点P在射线 上匀速运动,运动的过程中以P为对称中心,O为一个顶点作正方形 ,当正方形 的面积为40时,点A的坐标是( )
9. 如图,点 ,点P在射线 上匀速运动,运动的过程中以P为对称中心,O为一个顶点作正方形 ,当正方形 的面积为40时,点A的坐标是( )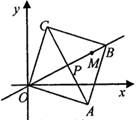 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
10. 计算: = .11. 在菱形ABCD中,对角线AC,BD的长分别是6和8,则菱形的周长是 .
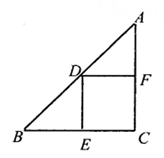
12. 已知一个样本的方差 ,则此样本的平均数是.13. 直线 与 平行,且经过 ,则 .14. 如图,正方形 的边长为12,点P在 边上且 ,点Q是 上一动点,则 的最小值为. 15. 如图,点A,D分别在两条直线 和 上, ∥x轴,已知B,C都在x轴上,且四边形 是矩形,则 的值为.
15. 如图,点A,D分别在两条直线 和 上, ∥x轴,已知B,C都在x轴上,且四边形 是矩形,则 的值为.
三、解答题
-
16. 计算: .17. 如图,在 中, , ,点D,E ,F分别为 , , 边上的中点,连接 , .求证:四边形 为正方形.
 18. 如图,已知直线 ,直线 相交于点A,直线 与x轴交于点 .
18. 如图,已知直线 ,直线 相交于点A,直线 与x轴交于点 . (1)、求直线 的解析式和点A的坐标;(2)、直接写出关于x的不等式 的解集.19. 求证:直角三角形斜边上的中线等于斜边的一半.(画出图形,写出已知、求证,并证明)20. 如图,在 中, , , .
(1)、求直线 的解析式和点A的坐标;(2)、直接写出关于x的不等式 的解集.19. 求证:直角三角形斜边上的中线等于斜边的一半.(画出图形,写出已知、求证,并证明)20. 如图,在 中, , , . (1)、用直尺和圆规在边 上找一点D,使D到 的距离等于 ;(2)、计算(1)中线段 的长.21. 近年来,共享单车逐渐成为大家日常生活中喜欢的“绿色出行”方式之一,为了解某地区居民出行使用共享单车的情况,随机调查了某天部分出行居民使用共享单车的情况,并整理成如下统计表:
(1)、用直尺和圆规在边 上找一点D,使D到 的距离等于 ;(2)、计算(1)中线段 的长.21. 近年来,共享单车逐渐成为大家日常生活中喜欢的“绿色出行”方式之一,为了解某地区居民出行使用共享单车的情况,随机调查了某天部分出行居民使用共享单车的情况,并整理成如下统计表:使用次数
0
1
2
3
4
5
人数
10
14
26
27
18
5
(1)、这天部分出行的居民使用共享单车次数的中位数是 , 众数是;(2)、这天部分出行居民平均每人使用共享单车多少次?(结果保留整数)(3)、若该地区某天有1500个居民出行,请你估计这天使用共享单车次数在3次以上(包含3次)的居民有多少人?22. 已知甲、乙两地相距840千米,客车、货车分别从甲、乙两地同时出发,匀速相向行驶.货车2小时可到达途中丙站,客车需9小时到达丙站(如图1所示),货车的速度是客车的 ,客、货车到丙站的距离分别为 、 (千米),它们与行驶时间x(时间)之间的函数关系如图2所示. (1)、求客、货两车的速度;(2)、如图2,两函数图象交于点E,求E点坐标.23. 如图,在正方形 中,点E迕射线 上,连接 ,作 ,且 交正方形外角的平分线 于点F.
(1)、求客、货两车的速度;(2)、如图2,两函数图象交于点E,求E点坐标.23. 如图,在正方形 中,点E迕射线 上,连接 ,作 ,且 交正方形外角的平分线 于点F. (1)、若点E在边 的中点处时, (填“>”“<”或“=”)(2)、若点E为边 上的任意一点(不含点B,C),探究此时 与 的数量关系,并说明理由.(3)、若点E是边 延长线上的一点,探究此时 与 的数量关系,并说明理由.24. 如图,四边形 为矩形,点A在y轴上,点C在x轴上,点B的坐标为 ,矩形 沿直线 折叠,使得点A恰好落在 边上的G处,E ,F分别在 , 上,已知点F的横坐标为4.
(1)、若点E在边 的中点处时, (填“>”“<”或“=”)(2)、若点E为边 上的任意一点(不含点B,C),探究此时 与 的数量关系,并说明理由.(3)、若点E是边 延长线上的一点,探究此时 与 的数量关系,并说明理由.24. 如图,四边形 为矩形,点A在y轴上,点C在x轴上,点B的坐标为 ,矩形 沿直线 折叠,使得点A恰好落在 边上的G处,E ,F分别在 , 上,已知点F的横坐标为4. (1)、求出 的长;(2)、求出直线 的解析式;(3)、点M在x轴上,直线 上是否存在点N,使以M,N,F ,G为顶点,且 为边的四边形为平行四边形?若存在,请求出N点的坐标;若不存在,请说明理由.
(1)、求出 的长;(2)、求出直线 的解析式;(3)、点M在x轴上,直线 上是否存在点N,使以M,N,F ,G为顶点,且 为边的四边形为平行四边形?若存在,请求出N点的坐标;若不存在,请说明理由.