浙江省绍兴市新昌县2020-2021学年八年级上学期数学阶段性测试(二)
试卷更新日期:2021-06-24 类型:月考试卷
一、单选题
-
1. 从长为3cm,6cm,8cm,9cm的四条线段中任选三条线段,不能组成一个三角形的为( )A、3cm,6cm,8cm B、3cm,8cm,9cm C、3cm,6cm,9cm D、6cm,8cm,9cm2. 如图,笑脸盖住的点的坐标可能为( )
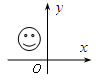 A、(-2,3) B、(3,-4) C、(-4,-6) D、(5,2)3. 把不等式组 的解集表示在数轴上,下列选项正确的是( )A、
A、(-2,3) B、(3,-4) C、(-4,-6) D、(5,2)3. 把不等式组 的解集表示在数轴上,下列选项正确的是( )A、 B、
B、 C、
C、 D、
D、 4. 能说明命题“如果两个角互补,那么这两个角一个是锐角,另一个是钝角”为假命题的两个角是( )A、120°,60° B、95°,105° C、30°,60° D、90°,90°5. 如图,△ABC中AC边上的高是哪条垂线段.( )
4. 能说明命题“如果两个角互补,那么这两个角一个是锐角,另一个是钝角”为假命题的两个角是( )A、120°,60° B、95°,105° C、30°,60° D、90°,90°5. 如图,△ABC中AC边上的高是哪条垂线段.( ) A、AE B、CD C、BF D、AF6. 工人师傅常用直角尺平分一个角,做法如下:如图所示,在∠AOB的边OA,OB上分别取OM=ON,移动直角尺,使直角尺两边相同的刻度分别与M,N重合(即CM=CN).此时过直角尺顶点C的射线OC即是∠AOB的平分线.这种做法的道理是( )
A、AE B、CD C、BF D、AF6. 工人师傅常用直角尺平分一个角,做法如下:如图所示,在∠AOB的边OA,OB上分别取OM=ON,移动直角尺,使直角尺两边相同的刻度分别与M,N重合(即CM=CN).此时过直角尺顶点C的射线OC即是∠AOB的平分线.这种做法的道理是( )
 A、HL B、SAS C、SSS D、ASA7. 已知点P到x轴距离为3,到y轴的距离为2,则P点坐标一定为( )A、(3,2) B、(2,3) C、(-3,-2) D、以上答案都不对8. 若正比例函数y=2mx的图象经过点A(x1 , y1)和点B(x2 , y2),当x1<x2时,y1>y2 , 则m的取值范围是( )A、m<0 B、m>0 C、m< D、m>9. 如图所示,在Rt△ABC中,∠C=90°,EF//AB,∠CEF=50°,则∠B的度数为( )
A、HL B、SAS C、SSS D、ASA7. 已知点P到x轴距离为3,到y轴的距离为2,则P点坐标一定为( )A、(3,2) B、(2,3) C、(-3,-2) D、以上答案都不对8. 若正比例函数y=2mx的图象经过点A(x1 , y1)和点B(x2 , y2),当x1<x2时,y1>y2 , 则m的取值范围是( )A、m<0 B、m>0 C、m< D、m>9. 如图所示,在Rt△ABC中,∠C=90°,EF//AB,∠CEF=50°,则∠B的度数为( ) A、50° B、60° C、30° D、40°10. 如图,当 时,自变量 x 的范围是( )
A、50° B、60° C、30° D、40°10. 如图,当 时,自变量 x 的范围是( )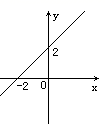 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 已知等腰三角形的两条边长分别为2和5,则它的周长为 .12. 命题“对顶角相等”改写成如果 , 那么.13. 在Rt△ABC中,锐角∠A=35°,则另一个锐角∠B= .14. 如图,一副分别含有 和 角的两个直角三角板,拼成如图所示的图形,其中 , , ,则 度.
 15. 函数y= 中,自变量x的取值范围是 .16. 如图,在锐角△ABC中,AB= ,∠BAC=45°,∠BAC的平分线交BC于点D,M,N分别是AD和AB上的动点,则BM+MN的最小值是.
15. 函数y= 中,自变量x的取值范围是 .16. 如图,在锐角△ABC中,AB= ,∠BAC=45°,∠BAC的平分线交BC于点D,M,N分别是AD和AB上的动点,则BM+MN的最小值是.
三、解答题
-
17. 解不等式组,并在数轴上表示解集.(1)、(2)、18. 为了了解小学生的体能情况,抽取了某校一个年级的部分学生进行一分钟跳绳次数的测试,将所得数据整理后,画出频率分布直方图如图所示.已知图中从左到右前三个小组的频率分别是0.1,0.3,0.4,第一小组的频数为5
 (1)、求第四小组的频率.(2)、问参加这次测试的学生数是多少?(3)、若次数在75次以上(含75次)为达标,试估计该年级学生跳绳测试的达标人数是多少人?19.
(1)、求第四小组的频率.(2)、问参加这次测试的学生数是多少?(3)、若次数在75次以上(含75次)为达标,试估计该年级学生跳绳测试的达标人数是多少人?19.如图所示,107国道OA和320国道OB在某巿相交于O点,在∠AOB的内部有工厂C和D,现要建一个货站P,使P到OA和OB的距离相等,且使PC=PD,用尺规作出P点的位置.(不写作法,保留作图痕迹,写出结论)
 20. AC,BD相交于点O,AO=OC,再添加一个什么条件,使两个三角形全等?
20. AC,BD相交于点O,AO=OC,再添加一个什么条件,使两个三角形全等? 21. 如图,∠A=∠B=90°,E是线段AB上一点,且AE=BC,∠1=∠2 .
21. 如图,∠A=∠B=90°,E是线段AB上一点,且AE=BC,∠1=∠2 . (1)、求证: ≌ ;(2)、若CD=10,求 的面积.22. 如图,已知直线y=kx+b经过点A(5,0),B(1,4).
(1)、求证: ≌ ;(2)、若CD=10,求 的面积.22. 如图,已知直线y=kx+b经过点A(5,0),B(1,4).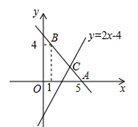 (1)、求直线AB的解析式;(2)、若直线y=2x-4与直线AB相交于点C,求点C的坐标.23. “一带一路”国家某食品加工厂需要一批食品包装盒,供应这种包装盒有两种方案选择:
(1)、求直线AB的解析式;(2)、若直线y=2x-4与直线AB相交于点C,求点C的坐标.23. “一带一路”国家某食品加工厂需要一批食品包装盒,供应这种包装盒有两种方案选择:方案一:从包装盒加工厂直接购买,购买所需的费 与包装盒数 满足如图1所示的函数关系.
方案二:租赁机器自己加工,所需费用 (包括租赁机器的费用和生产包装盒的费用)与包装盒数x满足如图2所示的函数关系.根据图象回答下列问题:
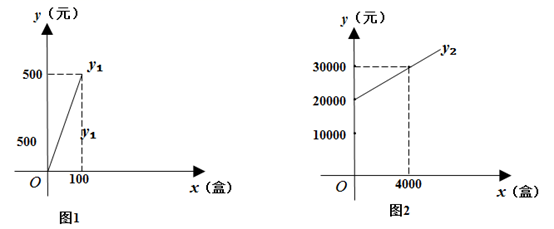 (1)、方案一中每个包装盒的价格是多少元?(2)、方案二中租赁机器的费用是多少元?生产一个包装盒的费用是多少元?(3)、请分别求出 、 与x的函数关系式(4)、如果你是决策者,你认为应该选择哪种方案更省钱?并说明理由
(1)、方案一中每个包装盒的价格是多少元?(2)、方案二中租赁机器的费用是多少元?生产一个包装盒的费用是多少元?(3)、请分别求出 、 与x的函数关系式(4)、如果你是决策者,你认为应该选择哪种方案更省钱?并说明理由