四川省泸州市合江县第六片区2020-2021学年八年级上学期数学第二次月考试卷
试卷更新日期:2021-06-24 类型:月考试卷
一、单选题
-
1. 下列图形中,不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 已知三角形两边的长分别是3和6,则此三角形第三边的长可能是( )A、1 B、3 C、8 D、103. 下列运算正确的是( )A、a2•a2=2a2 B、a2+a2=a4 C、(1+2a)2=1+2a+4a2 D、(﹣a+1)(a+1)=1﹣a24. 一个多边形的外角和是内角和的一半,这个多边形的边数是( )A、4 B、5 C、6 D、85. 多项式 与多项式 的公因式是( )A、 B、 C、 D、6. 如图,在△ABC中,AB=AC,D为BC上一点,且DA=DC,BD=BA,则∠B的大小为( )
2. 已知三角形两边的长分别是3和6,则此三角形第三边的长可能是( )A、1 B、3 C、8 D、103. 下列运算正确的是( )A、a2•a2=2a2 B、a2+a2=a4 C、(1+2a)2=1+2a+4a2 D、(﹣a+1)(a+1)=1﹣a24. 一个多边形的外角和是内角和的一半,这个多边形的边数是( )A、4 B、5 C、6 D、85. 多项式 与多项式 的公因式是( )A、 B、 C、 D、6. 如图,在△ABC中,AB=AC,D为BC上一点,且DA=DC,BD=BA,则∠B的大小为( )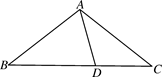 A、40° B、36° C、30° D、25°7. 计算(﹣ )2020×( )2021=( )A、﹣1 B、﹣ C、1 D、8. 如图,△ABC中,∠ACB=90°,沿CD折叠△CBD,使点B恰好落在AC边上的点E处.若∠A=22°,则∠BDC等于( )
A、40° B、36° C、30° D、25°7. 计算(﹣ )2020×( )2021=( )A、﹣1 B、﹣ C、1 D、8. 如图,△ABC中,∠ACB=90°,沿CD折叠△CBD,使点B恰好落在AC边上的点E处.若∠A=22°,则∠BDC等于( )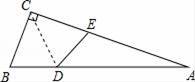 A、44° B、60° C、67° D、77°9. 下列各式中:① ;② ;③ ;④ ;⑤ .能用完全平方公式分解的个数有( )A、5个 B、4 个 C、3 个 D、2个10. 如果一个正多边形的内角和等于1080°,那么该正多边形的一个外角等于( )A、30° B、45° C、60° D、72°11. 如图,在 中, 是 的垂直平分线, ,且 的周长是 ,则 的周长为( )
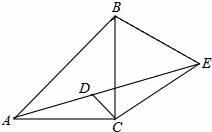
A、44° B、60° C、67° D、77°9. 下列各式中:① ;② ;③ ;④ ;⑤ .能用完全平方公式分解的个数有( )A、5个 B、4 个 C、3 个 D、2个10. 如果一个正多边形的内角和等于1080°,那么该正多边形的一个外角等于( )A、30° B、45° C、60° D、72°11. 如图,在 中, 是 的垂直平分线, ,且 的周长是 ,则 的周长为( ) A、 B、 C、 D、12. 如图, AD是 的中线,E、F分别是AD和AD延长线上的点,且 ,连结BF、CE . 下列说法:①CE=BF②△ABD和△ACD面积相等;③BF∥CE;④△BDF≌△CDE.其中正确的有( )
A、 B、 C、 D、12. 如图, AD是 的中线,E、F分别是AD和AD延长线上的点,且 ,连结BF、CE . 下列说法:①CE=BF②△ABD和△ACD面积相等;③BF∥CE;④△BDF≌△CDE.其中正确的有( )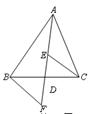 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
13. 如图,已知 = = , 于点B, = , = , = ,则 =
 14. 在平面直角坐标系中,点A(2,3)与点B关于x轴对称,则点B的坐标为 .15. 分解因式: =.16. 如图,钝角三角形△ABC的面积是15,最长边AB=10,BD平分∠ABC , 点M , N分别是BD , BC上的动点,则CM+MN的最小值为
14. 在平面直角坐标系中,点A(2,3)与点B关于x轴对称,则点B的坐标为 .15. 分解因式: =.16. 如图,钝角三角形△ABC的面积是15,最长边AB=10,BD平分∠ABC , 点M , N分别是BD , BC上的动点,则CM+MN的最小值为
三、解答题
-
17. 已知:如图,A、C、F、D在同一直线上, = , , = ,求证: △ABC ≌ △DEF
 18. 如图,在 中, 是高, 是角平分线, , 交于点F, = 0°, =70°,求 的度数
18. 如图,在 中, 是高, 是角平分线, , 交于点F, = 0°, =70°,求 的度数 19. 先化简,再求值:(a+3)2-(a+1)(a-1)-2(2a+4),其中a=-2.20. 如图,在长度为1个单位长度的小正方形组成的正方形网格中, ABC的三个顶点A、B、C都在格点上.
19. 先化简,再求值:(a+3)2-(a+1)(a-1)-2(2a+4),其中a=-2.20. 如图,在长度为1个单位长度的小正方形组成的正方形网格中, ABC的三个顶点A、B、C都在格点上.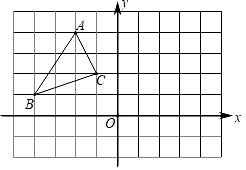
( 1 )在图中画出与 ABC关于直线y成轴对称的 A1B1C1;
( 2 )求 ABC的面积;
( 3 )在x轴上找出一点P,使得PB+PC的值最小.(不需计算,在图上直接标记出点P的位置)
21. 如图,在△ABC中,点D是边BC上的一点,点E是边AC上的一点,且AB=AC=DC , BD=CE , 连接AD、DE .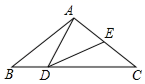 (1)、求证:△ADE是等腰三角形;(2)、若∠ADE=40°,请求出∠BAC的度数.22. 已知a,b,c是 的三边长,且满足 = , = ,求 的周长.
(1)、求证:△ADE是等腰三角形;(2)、若∠ADE=40°,请求出∠BAC的度数.22. 已知a,b,c是 的三边长,且满足 = , = ,求 的周长.