江苏省扬州市宝应县东北片2020-2021学年八年级上学期数学10月月考试卷
试卷更新日期：2021-06-24 类型：月考试卷
一、单选题
-
1. 下列倡导节约的图案中，是轴对称图形的是（ ）A、
B、
C、
D、
2. 已知△ABC≌△DEF，∠A=80°，∠E=40°，则∠F等于（ ）A、80° B、40° C、60° D、120°3. 如图，某同学把一块三角形的玻璃打碎成了三块，现在要到玻璃店去配一块完全一样的玻璃，那么，最省事的方法是（ ）
A、带①去 B、带②去 C、带③去 D、带①去和带②去4. 如图，工人师傅砌门时，常用木条EF固定矩形门框ABCD，使其不变形，这种做法的根据是（ ）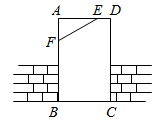
A、两点之间线段最短 B、矩形的对称性 C、矩形的四个角都是直角 D、三角形的稳定性5. 如图，在∠AOB的两边上，分别取OM=ON，再分别过点M、N作OA，OB的垂线，交点为P，画射线OP，则OP平分∠AOB的依据是（ ）
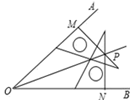A、HL B、SAS C、AAS D、SSS6. 如图是5×5的正方形网络，以点D，E为两个顶点作位置不同的格点三角形，使所作的格点三角形与△ABC全等，这样的格点三角形最多可以画出（ ）
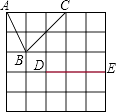A、2个 B、4个 C、6个 D、8个7. 如图所示，是一块三角形的草坪，现要在草坪上建一凉亭供大家休息，要使凉亭到草坪的三个顶点的距离相等，凉亭的位置应选在（ ）
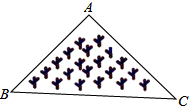A、△ABC三边的垂直平分线的交点 B、△ABC的三条中线的交点 C、△ABC三条角平分线的交点 D、△ABC三条高所在直线的交点8. 如图，△ABC中，∠ABC与∠ACB的平分线交于点F，过点F作DE∥BC交AB于点D，交AC于点E，那么下列结论：①△BDF和△CEF都是等腰三角形；②DE＝BD+CE；③△ADE的周长等于AB与AC的和；④BF＝CF.其中正确的有（ ）
A、①②③ B、①②③④ C、①② D、①二、填空题
-
9. 一辆汽车的牌照在车下方水坑中的像是
，则这辆汽车的牌照号码应为.
10. 如图，BC=EF，AC∥DF。请你添加一个适当的条件，使得△ABC≌△DEF。（只需填一个答案即可)
11. 如图，Rt△ABC中，∠ACB＝90°，点D为斜边AB的中点，CD＝6cm，则AB的长为cm.
12. 如图，已知AB∥CF，E为DF的中点.若AB＝13cm，CF＝7cm，则BD＝cm.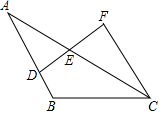
13. 如图，把一张矩形纸片ABCD沿对角线BD折叠，使C点落在C′，且BC′与AD交于E点，若∠ABE=40°，则∠ADB=.
14. 如图，在Rt△ABC中，∠BAC＝90°，AB＝AC，分别过点B，C作过点A的直线的垂线BD，CE，若BD＝4cm，CE＝3cm，则DE＝cm.
15. 在等腰三角形中，已知一个角为40°，那么另两个角的度数是.16. 如图所示的网格是正方形网格，图形的各个顶点均为格点，则∠1+∠2=.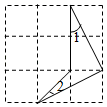
17. 如图，△ABC中，∠BAC=110°，AB、AC的垂直平分线分别交BC于点E、F，则∠EAF的度数为.
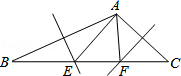18. 如图，O是等边三角形ABC内一点，∠AOB＝110°，∠BOC＝m°，D是△ABC外一点，且△ADC≌△BOC，连接OD.当m为时，△AOD是等腰三角形.
三、解答题
-
19. 如图，点D在AB上，点E在AC上，AB=AC，AD=AE，试说明∠B=∠C；
20. 在下列各图中分别补一个小正方形，使其成为不同的轴对称图形．
21. 如图，△ABC中，AB=AC，点E，F在边BC上，BE=CF，点D在AF的延长线上，AD=AC．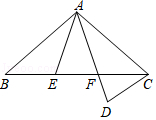
(1)、求证：△ABE≌△ACF；
(2)、若∠BAE=30°，则∠ADC=°．
22. 如图，已知∠AOB＝20°，点C是AO上一点，在射线OB上求作一点F，使得∠CFO＝40°.（尺规作图，保留作图痕迹，并说明理由）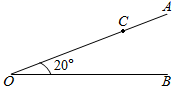
23. 已知：如图，AB＝AC，∠ABD＝∠ACD.求证：DB＝DC.
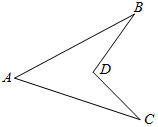24. 作图题：如图，在10×10的正方形网格中，每个小正方形的边长都为1，网格中有一个格点△ABC（即三角形的顶点都在格点上）.
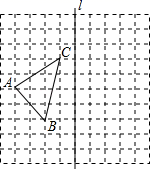
（ 1 ）在图中画出△ABC关于直线l对称的△A1B1C1；
（要求：A与A1 ， B与B1 ， C与C1相对应）
（ 2 ）求出△A1B1C1面积.
（ 3 ）在直线l上找一点P，使得PA+PB的值最小.
25. 如图所示，在△ABC中，∠C＝90°，AD是∠BAC的平分线，DE⊥AB交AB于点E，点F在AC上，BD＝DF.
求证：
(1)、CF＝EB；(2)、AB＝AF＋2EB.26. 如图：已知线段AB和射线BM交于点B，直线AN过点A且满足AN BM.
(1)、利用尺规完成以下作图，并保留作图痕迹（不写作法）.①在射线BM上作一点C，使BC＝BA.
②作∠ABM的角平分线交直线AN于D点.
(2)、在（1）所作的图形中，连接AC，求证：AD＝BC.27. 如图，C为线段AB上任意一点（不与A、B重合）分别以AC、BC为一边在AB的同侧作等边△ACD和等边△BCE，连接AE交CD于点M，连接BD交CE于点N.AE与BD交于点P.连接PC.试说明：
(1)、△ACE≌△DCB.(2)、∠APD的度数.(3)、∠APC＝∠BPC.28. 阅读理解如图①，△ABC 中，沿∠BAC 的平分线 AB1 折叠，剪掉重复部分；将余下部分沿∠B1A1C 的平分线 A1B2 折叠，剪掉重复部分；….；将余下部分沿∠BnAnC 的平分线 AnBn+1 折叠， 点 Bn 与点 C 重合.无论折叠多少次，只要最后一次恰好重合，∠BAC 是△ABC 的好角. 小丽展示了确定∠BAC 是△ABC 的好角的两种情形.情形一：如图②，沿等腰三角形ABC 顶角∠BAC 的平分线 AB1 折叠，点 B 与点 C 重合；情形二：如图③，沿∠BAC 的平分线 AB1 折叠，剪掉重复部分；将余下的部分沿∠B1A1C 的平分线 A1B2 折叠，此时点 B1 与点 C 重合.
(1)、探究发现
△ABC 中，∠B=2∠C，∠BAC 是不是△ABC 的好角？（填“是”或“不是”）(2)、猜想：若经过 n 次折叠后发现∠BAC 是△ABC 的好角，则∠B 与∠C（不妨设∠B > ∠C ）之间的等量关系为；(3)、应用提升
小丽找到一个三角形，三个角分别为 15°、60°、105°，发现 60°和 105°的两个角都是此三角形的好角.请你完成，如果一个三角形的最小角是 12°，试求出三角形另外两个角的度数，使该三角形的三个角均是此三角形的好角.