江苏省苏州市吴江区北外2020-2021学年八年级上学期数学9月月考试卷
试卷更新日期:2021-06-24 类型:月考试卷
一、单选题
-
1. 绿化做得好,染污就减少;垃圾分类放,环境有保障,在以下绿色食品、回收、节能、节水四个标志中,轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 代数式 中x的取值范围是( )A、 B、 C、 D、3. 下列根式中是最简二次根式的是( )A、 B、 C、 D、4. 下列等式不成立的是( )A、 B、 C、 D、5. 在四个数 , , , 中,无理数的个数是( )A、0 B、1 C、2 D、36. 如图, , ,如果根据“ ”判定 ,那么需要补充的条件是( )
2. 代数式 中x的取值范围是( )A、 B、 C、 D、3. 下列根式中是最简二次根式的是( )A、 B、 C、 D、4. 下列等式不成立的是( )A、 B、 C、 D、5. 在四个数 , , , 中,无理数的个数是( )A、0 B、1 C、2 D、36. 如图, , ,如果根据“ ”判定 ,那么需要补充的条件是( )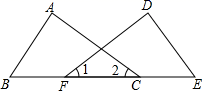 A、 B、 C、 D、7. 下列给出的三条线段的长,能组成直角三角形的是( )A、 B、 C、 D、8. 如图,矩形 中, , , 在数轴上,若以点A为圆心,对角线 的长为半径作弧交数轴于点M,则点M表示的数为( )
A、 B、 C、 D、7. 下列给出的三条线段的长,能组成直角三角形的是( )A、 B、 C、 D、8. 如图,矩形 中, , , 在数轴上,若以点A为圆心,对角线 的长为半径作弧交数轴于点M,则点M表示的数为( ) A、 B、 C、 D、9. 在正方形网格中每个小正方形的边长都是1,已知线段 ,以 为腰画等腰 ,则顶点C共有( )个.
A、 B、 C、 D、9. 在正方形网格中每个小正方形的边长都是1,已知线段 ,以 为腰画等腰 ,则顶点C共有( )个. A、5个 B、6个 C、7个 D、8个10. 汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图”,后人称其为“赵爽弦图”.如图是由弦图变化得到的,它由八个全等的直角三角形拼接而成,记图中正方形ABCD、正方形EFGH、正方形MNKT的面积分别为S1、S2、S3.若S1+S2+S3=10,则S2的值为( )
A、5个 B、6个 C、7个 D、8个10. 汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图”,后人称其为“赵爽弦图”.如图是由弦图变化得到的,它由八个全等的直角三角形拼接而成,记图中正方形ABCD、正方形EFGH、正方形MNKT的面积分别为S1、S2、S3.若S1+S2+S3=10,则S2的值为( )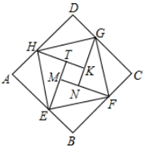 A、 B、 C、3 D、
A、 B、 C、3 D、二、填空题
-
11. -64的立方根是 。12. 比较大小: .13. 计算 .14. 有一个数值转换机,原理如下:

当输入的 时,输出的 .
15. 化简 的结果是.16. “三等分角”大约是在公元前五世纪由古希腊人提出来的,借助如图所示的“三等分角仪”能三等分任一角.这个三等分角仪由两根有槽的棒OA,OB组成,两根棒在O点相连并可绕O转动,C点固定,OC=CD=DE,点D、E可在槽中滑动.若∠BDE=75°,则∠CDE的度数是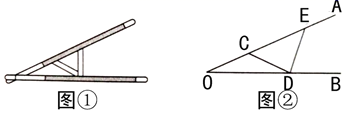 17. 如图,在四边形 中, ,点E是 的中点.若 , ,则 .
17. 如图,在四边形 中, ,点E是 的中点.若 , ,则 . 18. 如图,在 中, , ,O是 的中点,如果在 和 上分别有一个动点M、N在移动,且在移动时保持 .若 .则 的最小值为.
18. 如图,在 中, , ,O是 的中点,如果在 和 上分别有一个动点M、N在移动,且在移动时保持 .若 .则 的最小值为.
三、解答题
-
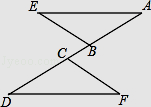
19. 计算:(1)、(2)、20. 求下列各题中的x(1)、(2)、21. 已知:如图,点A、B、C、D在同一条直线上,AC=DB,∠ABE=∠DCF,BE=CF,求证:AE∥DF.
 22. 如图,花果山上有两只猴子在一棵树 上的点B处,且 ,它们都要到A处吃东西,其中一只猴子甲沿树爬下走到离树 处的A处,另一只猴子乙先爬到项D处后再沿缆绳 滑到A处.已知两只猴子所经过的路程相等,设 为 .求这棵树高有多少米?
22. 如图,花果山上有两只猴子在一棵树 上的点B处,且 ,它们都要到A处吃东西,其中一只猴子甲沿树爬下走到离树 处的A处,另一只猴子乙先爬到项D处后再沿缆绳 滑到A处.已知两只猴子所经过的路程相等,设 为 .求这棵树高有多少米? 23. 在 的正方形网格中,已将图中的四个小正方形涂上阴影,若再从其余小正方形中任选一个也涂上阴影,使整个阴影部分组成的图形成轴对称图形,请画出三种情形.
23. 在 的正方形网格中,已将图中的四个小正方形涂上阴影,若再从其余小正方形中任选一个也涂上阴影,使整个阴影部分组成的图形成轴对称图形,请画出三种情形. 24. 数学阅读是学生个体根据已有的知识经验,通过阅读数学材料建构数学意义和方法的学习活动,是学生主动获取信息,汲取知识,发展数学思维,学习数学语言的途径之一.请你先阅读下面的材料,然后再根据要求解答提出的问题:
24. 数学阅读是学生个体根据已有的知识经验,通过阅读数学材料建构数学意义和方法的学习活动,是学生主动获取信息,汲取知识,发展数学思维,学习数学语言的途径之一.请你先阅读下面的材料,然后再根据要求解答提出的问题:问题情境:设a,b是有理数,且满足 ,求 的值.
解:由题意得 ,
∵a,b都是有理数,
∴ 也是有理数,
∵ 是无理数,
∴ ,
∴ ,
∴
解决问题:设x,y都是有理数,且满足 ,求 的值.
25. 如图,在 中, , ,延长 至点D,使 ,连接 .以 为边作等腰直角三角形 ,其中 ,连接 .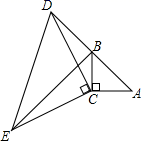 (1)、求证: ;(2)、若 ,求 的长.26. 如图,点P、Q分别是边长为4cm的等边△ABC边AB、BC上的动点,点P从顶点A,点Q从顶点B同时出发,且它们的速度都为1cm/s.
(1)、求证: ;(2)、若 ,求 的长.26. 如图,点P、Q分别是边长为4cm的等边△ABC边AB、BC上的动点,点P从顶点A,点Q从顶点B同时出发,且它们的速度都为1cm/s. (1)、连接AQ、CP交于点M,则在P、Q运动的过程中,∠CMQ变化吗?若变化,则说明理由,若不变,则求出它的度数;(2)、请求出何时△PBQ是直角三角形?
(1)、连接AQ、CP交于点M,则在P、Q运动的过程中,∠CMQ变化吗?若变化,则说明理由,若不变,则求出它的度数;(2)、请求出何时△PBQ是直角三角形?

