广西北部湾经济区2020-2021学年八年级上学期数学第二次月考试卷
试卷更新日期:2021-06-24 类型:月考试卷
一、单选题
-
1. 如图,盖房子时,在窗框没有安装之前,木工师傅常常先在窗框上斜钉一根木条,使其不变形,这种做法的根据是( )
 A、两点之间线段最短 B、长方形的对称性 C、长方形四个角都是直角 D、三角形的稳定性2. 下列图案中,是轴对称图形的是( )A、
A、两点之间线段最短 B、长方形的对称性 C、长方形四个角都是直角 D、三角形的稳定性2. 下列图案中,是轴对称图形的是( )A、 B、
B、 C、
C、 D、
D、 3. 以下列各组线段为边,能组成三角形的是( )A、1,2,3 B、2,3,4 C、2,5,8 D、6,3,34. 点P(3,-1)关于x轴对称的点的坐标是( )A、(-3,1) B、(-3,-1) C、(1,-3) D、(3,1)5. 下列说法正确的是( )A、形状相同的两个三角形全等 B、两边和一角对应相等的两个三角形全等 C、三个角对应相等的两个三角形全等 D、两条直角边对应相等的两个直角三角形全等6. 如图,在△ABD和△ACD中,∠1=∠2,AB=AC,那么△ABD≌△ACD的依据是( )
3. 以下列各组线段为边,能组成三角形的是( )A、1,2,3 B、2,3,4 C、2,5,8 D、6,3,34. 点P(3,-1)关于x轴对称的点的坐标是( )A、(-3,1) B、(-3,-1) C、(1,-3) D、(3,1)5. 下列说法正确的是( )A、形状相同的两个三角形全等 B、两边和一角对应相等的两个三角形全等 C、三个角对应相等的两个三角形全等 D、两条直角边对应相等的两个直角三角形全等6. 如图,在△ABD和△ACD中,∠1=∠2,AB=AC,那么△ABD≌△ACD的依据是( )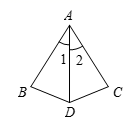 A、SAS B、AAS C、ASA D、SSS7. 某同学把一块三角形的玻璃打碎成了3块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事方法是( )
A、SAS B、AAS C、ASA D、SSS7. 某同学把一块三角形的玻璃打碎成了3块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事方法是( )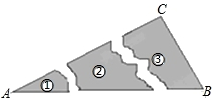 A、带①去 B、带②去 C、带③去 D、①②③都带去8. 如图,直线 与x轴交于点 ,与y轴交于点 ,则关于x的不等式 的解集为( )
A、带①去 B、带②去 C、带③去 D、①②③都带去8. 如图,直线 与x轴交于点 ,与y轴交于点 ,则关于x的不等式 的解集为( ) A、 B、 C、 D、9. 如图,点B、C、E在一条直线上, , , ,则下列结论中,不正确的是( )
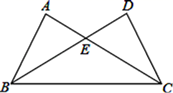
A、 B、 C、 D、9. 如图,点B、C、E在一条直线上, , , ,则下列结论中,不正确的是( ) A、 与 互为余角 B、 C、 D、10. 如图, 是线段 的垂直平分线,则图中全等三角形的对数有( )
A、 与 互为余角 B、 C、 D、10. 如图, 是线段 的垂直平分线,则图中全等三角形的对数有( ) A、2对 B、3对 C、4对 D、5对11. 正比例函数 与一次函数 在同一坐标系中的图象大致是( )A、
A、2对 B、3对 C、4对 D、5对11. 正比例函数 与一次函数 在同一坐标系中的图象大致是( )A、 B、
B、 C、
C、 D、
D、 12. 如图,在 中, , , ,则 等于( )
12. 如图,在 中, , , ,则 等于( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 三角形的内角和为度.14. 函数 中自变量x的取值范围是.15. 如图,点B、A、D、E在同一直线上, , ,要使 ,需添加一个适当的条件是.(只填一个即可)
 16. ”两个全等的三角形的周长相等“的逆命题是命题。(填”真“或”假“)。17. 如图, 中,D是 上的一点, 交 于点E, , ,若四边形 的面积是 ,则 的面积为 .
16. ”两个全等的三角形的周长相等“的逆命题是命题。(填”真“或”假“)。17. 如图, 中,D是 上的一点, 交 于点E, , ,若四边形 的面积是 ,则 的面积为 . 18. 如图,在 中, , , ,射线 于点A,点E、D分别在线段 和射线 上运动,并始终保持 ,要使 和 全等,则 的长为.
18. 如图,在 中, , , ,射线 于点A,点E、D分别在线段 和射线 上运动,并始终保持 ,要使 和 全等,则 的长为.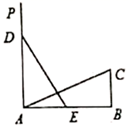
三、解答题
-
19. 如图,为了丰富群众的娱乐活动,某镇准备新建一个文化娱乐站,要求娱乐站到三个村A、B、C的距离相等,请你用尺规作图的方法确定娱乐站的位置(不写作法,保留作图痕迹)
 20. 一个多边形,它的内角和比外角和的3倍多180°,求这个多边形的边数及内角和度数.21. 如图,在平面直角坐标系中, 各顶点坐标为 , , ,分别画出 关于x轴、y轴对称的 和 .
20. 一个多边形,它的内角和比外角和的3倍多180°,求这个多边形的边数及内角和度数.21. 如图,在平面直角坐标系中, 各顶点坐标为 , , ,分别画出 关于x轴、y轴对称的 和 .
 22. 如图,在 中,边 的垂直平分线 交 于E,交 于D,若 , 的周长为 ,求 的周长.
22. 如图,在 中,边 的垂直平分线 交 于E,交 于D,若 , 的周长为 ,求 的周长.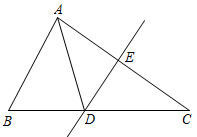 23. 如图,在 与 中, , , .
23. 如图,在 与 中, , , . (1)、求证: ;(2)、若 , ,求 的度数.
(1)、求证: ;(2)、若 , ,求 的度数.