湖南省娄底市2021年数学中考仿真模拟试卷（一）

试卷更新日期：2021-06-24 类型：中考模拟

进入出卷网下载

一、单选题

1. 2021的相反数是（）

A、 $- 2021$ B、 $- \frac{1}{2021}$ C、2021 D、 $\frac{1}{2021}$

查看试题解析
2. 下列计算正确的是（　　）

A、a²•a³＝a⁶ B、（x+y）²＝x²+y² C、（a⁵÷a²）²＝a⁶ D、（﹣3xy）²＝9xy²

查看试题解析
3. 入冬以来，全球新型冠状病毒肺炎疫情防控形势严峻，我们应该坚持“勤洗手，戴口罩，常通风”.一双没有洗过的手，带有各种细菌约75000万个，75000万用科学记数法表示为（　　）

A、7.5× $10^{4}$ B、7.5× $10^{5}$ C、7.5× $10^{8}$ D、7.5× $10^{9}$

查看试题解析
4. 下列图形中是轴对称图形但不是中心对称图形的是（　　）

A、 B、 C、 D、

查看试题解析
5. 演讲比赛共有9位评委分别给出某选手的原始评分，评定该选手的成绩时，从9个原始评分中去掉1个最高分、1个最低分，得到7个有效评分.7个有效评分与9个原始评分相比，不变的数字特征是（）

A、平均数 B、中位数 C、众数 D、方差

查看试题解析
6. 已知点P（a，b）在反比例函数 $y = - \frac{5}{x}$ 的图象上，点M（﹣b，a）在反比例函数 $y = \frac{k}{x}$ 的图象上，则k的值为（　　）

A、﹣5 B、5 C、 $\frac{1}{5}$ D、无法确定

查看试题解析
7. 下列命题是假命题的是（）

A、对角线互相垂直且相等的平行四边形是正方形． B、对角线互相垂直的矩形是正方形． C、对角线相等的菱形是正方形． D、对角线互相垂直平分的四边形是正方形．

查看试题解析
8. 关于x的分式方程 $\frac{m}{x - 2}$ ﹣ $\frac{3}{2 - x}$ ＝1有增根，则m的值（）

A、m＝2 B、m＝1 C、m＝3 D、m＝﹣3

查看试题解析
9. 满足不等式组 ${\begin{array}{l} 5 x + 2 > 3 (x - 1) \\ \frac{1}{2} x - 1 \leq 7 - \frac{3}{2} x \end{array}$ 的非负整数解的个数为（）

A、4 B、5 C、6 D、7

查看试题解析
10. 已知正比例函数 $y = k x (k \neq 0)$ 的图象过点 $(2 ， 3)$ ，把正比例函数 $y = k x (k \neq 0)$ 的图象平移，使它过点 $(1 ， - 1)$ ，则平移后的函数图象大致是（）

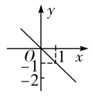A、 B、 C、 D、

查看试题解析
11. 如图，等边三角形 $A B C$ 内接于 $⊙ O$ ，若 $⊙ O$ 的半径为2，则图中阴影部分的面积等于（）

A、 $\frac{π}{3}$ B、 $\frac{2 π}{3}$ C、 $\frac{4 π}{3}$ D、 $2 π$

查看试题解析
12. 抛物线y＝ $-$ x²+bx+3的对称轴为直线x＝ $-$ 1．若关于x的一元二次方程 $-$ x²+bx+3﹣t＝0（t为实数）在﹣2＜x＜3的范围内有实数根，则t的取值范围是（）

A、 $-$ 12＜t≤3 B、 $-$ 12＜t＜4 C、 $-$ 12＜t≤4 D、 $-$ 12＜t＜3

查看试题解析

二、填空题

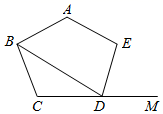
13. 关于x的一元二次方程 $x^{2} + m x - 5 = 0$ 有一根是 $x = - 1$ ，则另外一根是.

查看试题解析
14. 如图，在正五边形ABCDE中，DM是边CD的延长线，连接BD，则∠BDM的度数是.

查看试题解析
15. 如图，在△ABC中，∠ACB＝90°，∠ABC的平分线BD交AC于点D，已知AC＝3，AD＝2，则点D到AB边的距离为.

查看试题解析
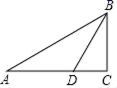16. 如图，每个灯泡能否通电发光的概率都是 $\frac{1}{2}$ ，当合上开关时，至少有一个灯泡发光的概率是.

查看试题解析
17. 观察下列图形：

它们是按一定规律排列的，依照此规律，用6064个五角星摆出的图案应该是第个图形.

查看试题解析
18. 已知 $\tan (α + β) = \frac{\tan α + \tan β}{1 - \tan α \cdot \tan β}$ ， $\tan 2 α = \frac{2 \tan α}{1 - \tan^{2} α}$ （其中 $α$ 和 $β$ 都表示角度），比如求 $\tan 105 °$ ，可利用公式得 $\tan 105 ° = \tan (60 ° + 45 °) = \frac{\sqrt{3} + 1}{1 - \sqrt{3}} = - \sqrt{3} - 2$ ，又如求 $\tan 120 °$ ，可利用公式得 $\tan 120 ° = \tan (2 \times 60 °) = \frac{2 \times \sqrt{3}}{1 - {(\sqrt{3})}^{2}} = - \sqrt{3}$ ，请你结合材料，若 $\tan (120 ° + λ) = - \frac{\sqrt{3}}{3}$ （ $λ$ 为锐角），则 $λ$ 的度数是．

查看试题解析

三、解答题

19. 计算： ${(- \frac{1}{2})}^{- 2}$ +2cos30°﹣|1﹣ $\sqrt{3}$ |+ ${(π - 2020)}^{0}$ .

查看试题解析
20. 先化简，再求值： $\frac{2}{a + 1}$ ﹣ $\frac{a - 2}{a^{2} - 1}$ ÷ $\frac{a - 2}{a^{2} - 2 a + 1}$ ，并在﹣1，1，2，3这四个数中取一个合适的数作为a的值代入求值.

查看试题解析
21. 某中学为了解九年级学生对新冠肺炎防控知识的掌握情况，从全校九年级学生中随机抽取部分学生进行调查.调查结果分为四类：A类—非常了解；B类—比较了解；C—一般了解；D类—不了解.现将调查结果绘制成如下不完整的统计图，请根据统计图中的信息解答下列问题：

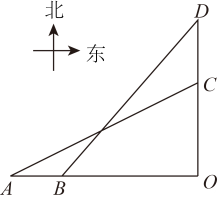
(1)、本次共调查了名学生；

(2)、补全条形统计图；

(3)、D类所对应扇形的圆心角的大小为；

(4)、若该校九年级学生共有500名，根据以上抽样结果，估计该校九年级学生对新冠肺炎防控知识非常了解的约有名.

查看试题解析
22. 如图，小岛 $C$ 和 $D$ 都在码头 $O$ 的正北方向上，它们之间距离为 $6.4 km$ ，一艘渔船自西向东匀速航行，行驶到位于码头 $O$ 的正西方向 $A$ 处时，测得 $∠ C A O = 26.5 °$ ，渔船速度为 $28 km / h$ ，经过 $0 .2h$ ，渔船行驶到了 $B$ 处，测得 $∠ D B O = 49 °$ ，求渔船在 $B$ 处时距离码头 $O$ 有多远？（结果精确到 $0.1 km$ ）
（参考数据： $\sin 26.5 ° \approx 0.45$ ， $\cos 26.5 ° \approx 0.89$ ， $\tan 26.5 ° \approx 0.50$ ， $\sin 49 ° \approx 0.75$ ， $\cos 49 ° \approx 0.66$ ， $\tan 49 ° \approx 1.15$ ）

查看试题解析
23. 随着中国传统节日“端午节”的临近，东方红商场决定开展“欢度端午，回馈顾客”的让利促销活动，对部分品牌粽子进行打折销售，其中甲品牌粽子打八折，乙品牌粽子打七五折，已知打折前，买6盒甲品牌粽子和3盒乙品牌粽子需600元；打折后，买50盒甲品牌粽子和40盒乙品牌粽子需要5200元．

(1)、打折前甲、乙两种品牌粽子每盒分别为多少元？

(2)、阳光敬老院需购买甲品牌粽子80盒，乙品牌粽子100盒，问打折后购买这批粽子比不打折节省了多少钱？

查看试题解析
24. 如图，菱形ABCD的对角线AC，BD相交于点O，E是AD的中点，点F，G在AB上，EF⊥AB，OG∥EF．

(1)、求证：四边形OEFG是矩形；

(2)、若AD=10，EF=4，求OE和BG的长．

查看试题解析
25. 已知，如图，AB是⊙O的直径，点C为⊙O上一点， $O F ⊥ A C$ 于点F，交⊙O于点E，AC交BE于点H，点D为OE延长线上的一点，且∠ODA=∠BEC.

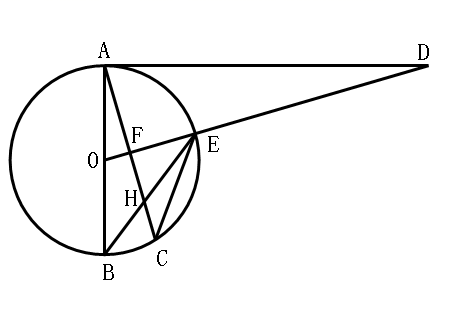(1)、求证：AD是⊙O的切线；

(2)、求证： $C E^{2} = E H \cdot B E$ ；

(3)、若⊙O的半径为5， $\cos ∠ A B E = \frac{4}{5}$ ，求AH的长.

查看试题解析
26. 如图所示，在平面直角坐标系中，抛物线 $y = a x^{2} + b x + c (a \neq 0)$ 的顶点坐标为 $C (3 ， 6)$ ，并与 $y$ 轴交于点 $B (0 ， 3)$ ，点 $A$ 是对称轴与 $x$ 轴的交点．

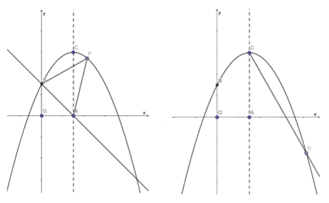(1)、求抛物线的解析式；

(2)、如图①所示， $P$ 是抛物线上的一个动点，且位于第一象限，连结BP、AP，求 $Δ A B P$ 的面积的最大值；

(3)、如图②所示，在对称轴 $A C$ 的右侧作 $∠ A C D = 30^{\circ}$ 交抛物线于点 $D$ ，求出 $D$ 点的坐标；并探究：在 $y$ 轴上是否存在点 $Q$ ，使 $∠ C Q D = 60^{\circ}$ ?若存在，求点 $Q$ 的坐标；若不存在，请说明理由．

查看试题解析