湖北省襄阳市襄城区2021年数学中考适应性考试试卷
试卷更新日期:2021-06-24 类型:中考模拟
一、单选题
-
1. 如图,数轴上被墨水遮盖的数可能为( )
 A、-4.2 B、-3 C、-1.5 D、-12. 一个等腰直角三角尺和一把直尺按如图所示的位置摆放,若 ,则∠2的度数是( )
A、-4.2 B、-3 C、-1.5 D、-12. 一个等腰直角三角尺和一把直尺按如图所示的位置摆放,若 ,则∠2的度数是( )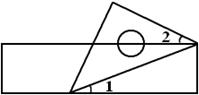 A、15° B、20° C、25° D、40°3. 下列运算正确的是( )A、 B、 C、 D、4. 下列说法不正确的是( )A、“汽车经过一个红绿灯路口时,前方正好是绿灯”是随机事件 B、对端午节期间市场上粽子质量情况的调查适合采用抽样调查 C、从一副扑克牌中随机抽取一张,它是红桃的概率是 D、一组数据的方差越大,则这组数据的波动也越大5. 如图是用八块相同的小正方体搭建的几何体,它的左视图是( )
A、15° B、20° C、25° D、40°3. 下列运算正确的是( )A、 B、 C、 D、4. 下列说法不正确的是( )A、“汽车经过一个红绿灯路口时,前方正好是绿灯”是随机事件 B、对端午节期间市场上粽子质量情况的调查适合采用抽样调查 C、从一副扑克牌中随机抽取一张,它是红桃的概率是 D、一组数据的方差越大,则这组数据的波动也越大5. 如图是用八块相同的小正方体搭建的几何体,它的左视图是( )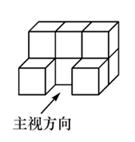 A、
A、 B、
B、 C、
C、 D、
D、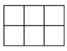 6. 已知点P(x-2,6-2x)是平面直角坐标系第二象限内一点,则x的取值范围在数轴上表示正确的是( )A、
6. 已知点P(x-2,6-2x)是平面直角坐标系第二象限内一点,则x的取值范围在数轴上表示正确的是( )A、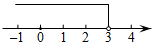 B、
B、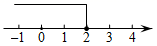 C、
C、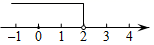 D、
D、 7. 如图,在平行四边形 中,点E是边 上一点,且 , 交对角线 于点F,则 等于( )
7. 如图,在平行四边形 中,点E是边 上一点,且 , 交对角线 于点F,则 等于( )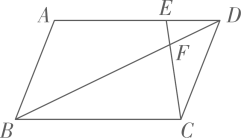 A、 B、 C、 D、8. 若 且 ,则函数 的图象可能是( )A、
A、 B、 C、 D、8. 若 且 ,则函数 的图象可能是( )A、 B、
B、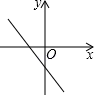 C、
C、 D、
D、 9. 如图,AB为⊙O的直径,点C为⊙O上的一点,过点C作⊙O的切线,交直径AB的延长线于点D,若∠A=25°,则∠D的度数是( )
9. 如图,AB为⊙O的直径,点C为⊙O上的一点,过点C作⊙O的切线,交直径AB的延长线于点D,若∠A=25°,则∠D的度数是( ) A、25° B、40° C、50° D、65°10. 小敏在某次投篮中,球的运动路线是抛物线y=﹣ x2+3.5的一部分(如图),若命中篮圈中心,则他与篮底的距离L是( )
A、25° B、40° C、50° D、65°10. 小敏在某次投篮中,球的运动路线是抛物线y=﹣ x2+3.5的一部分(如图),若命中篮圈中心,则他与篮底的距离L是( )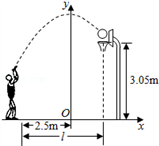 A、3.5m B、4m C、4.5m D、4.6m
A、3.5m B、4m C、4.5m D、4.6m二、填空题
-
11. 已知y=1+ + ,则2x+3y的算术平方根为.12. 四张背面完全相同的卡片上分别印有等腰三角形、平行四边形、正方形、圆,现将印有图形的一面朝下,混合均匀后从中随机抽取两张,则抽到的卡片上印有的图形既是轴对称图形又是中心对称图形的概率是.13. 如图,D、E分别是AC和AB上的点,AD=DC=8,DE=6,DE∥BC,∠C=90°,将△ADE沿着AB边向右平移,当点D落在BC上时,平移的距离为.
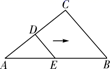 14. 《九章算术》中记录的一道题译为白话文是:把一份文件用慢马送到900里外的城市,需要的时间比规定时间多一天,如果用快马送,所需的时间比规定时间少3天,已知快马的速度是慢马的2倍,求规定时间.设规定时间为x天,则可列方程为.15. 如图,点M 为矩形ABCD的边BC上一点,将矩形ABCD沿AM折叠,使点B落在边CD上的点E处,EB交AM于点F,在EA上取点G,使EG=EC.若GF=6,sin∠GFE= ,则AB= .
14. 《九章算术》中记录的一道题译为白话文是:把一份文件用慢马送到900里外的城市,需要的时间比规定时间多一天,如果用快马送,所需的时间比规定时间少3天,已知快马的速度是慢马的2倍,求规定时间.设规定时间为x天,则可列方程为.15. 如图,点M 为矩形ABCD的边BC上一点,将矩形ABCD沿AM折叠,使点B落在边CD上的点E处,EB交AM于点F,在EA上取点G,使EG=EC.若GF=6,sin∠GFE= ,则AB= .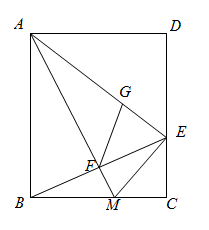
三、解答题
-
16. 先化简,再求值: ,其中 .17. 2020年注定是不平凡的一年,新年伊始,一场突如其来的疫情席卷全国.全国人民万众一心,战胜了疫情,“停课不停学”让“网络学习”成为了这一年春天一道别样的风景.某校为了解九年级学生居家网络学习情况,以便进行有针对性的教学安排,特对他们的网络学习时长(单位:小时)进行统计.现对随机抽取20名学生的数据进行分析:
收集数据:4.5,6,5.5,6.5,6.5,5.5,7,6,7.5,8,6.5,8,7.5,5.5,6.5,7,6.5,6,6.5,5
整理数据:
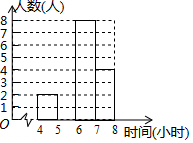
时长x(小时)
4<x≤5
5<x≤6
6<x≤7
7<x≤8
人 数
2
a
8
4
分析数据:
项 目
平均数
中位数
众 数
数 据
6.4
6.5
b
应用数据:
(1)、填空:a= , b=;(2)、请补全频数分布直方图;(3)、若九年级共有500人参与了网络学习,请估计学习时长在5<x≤7小时的人数.18. 如图,海面上一艘船由西向东航行,在A处测得正东方向上一座灯塔的最高点C的仰角为31°,再向东继续航行60m到达B处,测得该灯塔的最高点C的仰角为45°.根据测得的数据,计算这座灯塔的高度CD(结果取整数).参考数据:sin31°≈0.52,cos31°≈0.86,tan31°≈0.60 19. 有这样一个问题:探究函数 的图象与性质,并解决问题:小聪根据学习函数的经验,对问题进行了探究.下面是小聪的探究过程,请补充完整:(1)、函数 的自变量x的取值范围是;(2)、取几组y与x的对应值,填写在下表中,其中m的值为;
19. 有这样一个问题:探究函数 的图象与性质,并解决问题:小聪根据学习函数的经验,对问题进行了探究.下面是小聪的探究过程,请补充完整:(1)、函数 的自变量x的取值范围是;(2)、取几组y与x的对应值,填写在下表中,其中m的值为;x
…
-2
-1
0
3
4
…
y
…
1
2
3
6
6
m
1
…
(3)、如下图,根据(2)中表里各组对应值(x,y),在平面直角坐标系中描出了各点,画出了部分图象,请你把图象补充完整;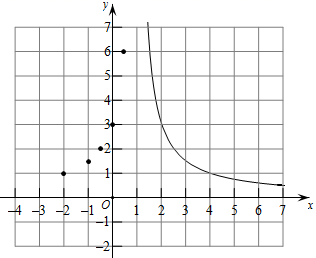 (4)、获得性质,解决问题:
(4)、获得性质,解决问题:①通过观察、分析、证明,可知函数 的图象是轴对称图形,它的对称轴是;
②若点M( , )、N( , )在函数 的图象上,且1< < ,则 (填 “ < ”或 “ > ”).
20. 如图,在四边形ABCD中,AB∥DC,AB=AD,对角线AC、BD交于点O,AC平分∠BAD.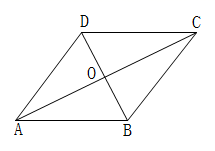 (1)、请用尺规作图过点C作CE⊥AB,垂足为点E(不写作法,保留作图痕迹);(2)、连接OE,若AB=2 ,BD=4,求OE的长.21. 如图,在△ABC中,∠C=90°,BE平分∠ABC交边AC于点E,点D在边AB上,以BD为直径作⊙O经过点E,交BC边于点F.
(1)、请用尺规作图过点C作CE⊥AB,垂足为点E(不写作法,保留作图痕迹);(2)、连接OE,若AB=2 ,BD=4,求OE的长.21. 如图,在△ABC中,∠C=90°,BE平分∠ABC交边AC于点E,点D在边AB上,以BD为直径作⊙O经过点E,交BC边于点F.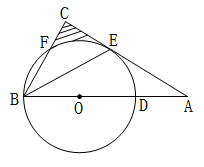 (1)、求证:AC是⊙O的切线;(2)、若BD=8,∠A=30°,求阴影部分的面积.22. 某蔬菜公司收购蔬菜进行销售的获利情况如下表所示:
(1)、求证:AC是⊙O的切线;(2)、若BD=8,∠A=30°,求阴影部分的面积.22. 某蔬菜公司收购蔬菜进行销售的获利情况如下表所示:销售方式
直接销售
粗加工后销售
精加工后销售
每吨获利(元)
100
250
450
现在该公司收购了140吨蔬菜,已知该公司每天能精加工蔬菜6吨或粗加工蔬菜16吨(两种加工不能同时进行)
(1)、如果要求在18天内全部销售完这140吨蔬菜,请完成下列表格:销售方式
全部直接销售
全部粗加工后销售
尽量精加工,剩余部分直接销售
获利(元)
(2)、如果先进行精加工,然后进行粗加工,要求15天刚好加工完140吨蔬菜,则应如何分配加工时间?(3)、若要求在不超过10天的时间,采用两种方式将140吨蔬菜加工完后销售,则加工这批蔬菜最多可获得多少利润?此时如何让安排时间?23. 如图1和 图2,四边形ABCD中,已知AD=DC,∠ADC=90°,点E、F分别在边AB、BC上,∠EDF=45°.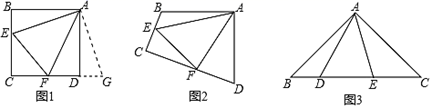 (1)、观察猜想:如图1,若∠A、∠DCB都是直角,把△DAE绕点D逆时针旋转90°至△DCG,使AD与DC重合,易得EF、AE、CF三条线段之间的数量关系,直接写出它们之间的关系式;(2)、类比探究:如图2,若∠A、∠C都不是直角,则当∠A与∠C满足数量关系时,EF、AE、CF三条线段仍有(1)中的关系,并说明理由;(3)、解决问题:如图3,在△ABC中,∠BAC=90°,AB=AC= ,点D、E均在边BC上,且∠DAE=45°,若BD=1,求AE的长.24. 如图,在平面直角坐标系中,抛物线 与x轴交于点A(-1,0)、点B(3,0),经过点A的一次函数 的图象与y轴正半轴交于点C,且与抛物线的另一个交点为D,△ABD的面积为5.
(1)、观察猜想:如图1,若∠A、∠DCB都是直角,把△DAE绕点D逆时针旋转90°至△DCG,使AD与DC重合,易得EF、AE、CF三条线段之间的数量关系,直接写出它们之间的关系式;(2)、类比探究:如图2,若∠A、∠C都不是直角,则当∠A与∠C满足数量关系时,EF、AE、CF三条线段仍有(1)中的关系,并说明理由;(3)、解决问题:如图3,在△ABC中,∠BAC=90°,AB=AC= ,点D、E均在边BC上,且∠DAE=45°,若BD=1,求AE的长.24. 如图,在平面直角坐标系中,抛物线 与x轴交于点A(-1,0)、点B(3,0),经过点A的一次函数 的图象与y轴正半轴交于点C,且与抛物线的另一个交点为D,△ABD的面积为5. (1)、求抛物线和一次函数的解析式;(2)、抛物线上的动点E在一次函数的图象下方,求△ACE面积的最大值,并求出此时点E的坐标;(3)、抛物线与y轴交于点F,抛物线的对称轴与抛物线交于点H,与x轴交于点G.若点Q为抛物线对称轴上一点,点P(c,0)为x轴上任意一点,且PQ⊥FQ,当点Q在线段GH(含端点)上运动时,求c的取值范围.
(1)、求抛物线和一次函数的解析式;(2)、抛物线上的动点E在一次函数的图象下方,求△ACE面积的最大值,并求出此时点E的坐标;(3)、抛物线与y轴交于点F,抛物线的对称轴与抛物线交于点H,与x轴交于点G.若点Q为抛物线对称轴上一点,点P(c,0)为x轴上任意一点,且PQ⊥FQ,当点Q在线段GH(含端点)上运动时,求c的取值范围.