湖北省随州市曾都区2021年年九年级下学期初中毕业升学适应性考试数学试卷
试卷更新日期:2021-06-24 类型:中考模拟
一、单选题
-
1. 下列各式中,结果是100的是( )A、 B、 C、 D、2. 下列运算正确的是( )A、 B、 C、 D、3. 如图,在 中,点D,E,F分别在边 , , 上,下列能判定 的条件是( )
 A、 B、 C、 D、4. 我国古代数学著作《九章算术》记载了一道有趣的问题,原文是:今有池方一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐.问水深、葭长各几何.译为:有一个水池,水面是一个边长为10尺的正方形,在水池正中央有一根芦苇,它高出水面1尺.如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面,水的深度与这根芦苇的长度分别是多少?设水深为x尺,根据题意,可列方程为( )
A、 B、 C、 D、4. 我国古代数学著作《九章算术》记载了一道有趣的问题,原文是:今有池方一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐.问水深、葭长各几何.译为:有一个水池,水面是一个边长为10尺的正方形,在水池正中央有一根芦苇,它高出水面1尺.如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面,水的深度与这根芦苇的长度分别是多少?设水深为x尺,根据题意,可列方程为( ) A、 B、 C、 D、5. 在体育中考训练中,男生小杰6次立定跳远的成绩(单位:米)如下:2.4,2.3,2.6,2.4,2.2,2.5,关于这组数据,下列结论不正确的是( )A、众数是2.4 B、中位数是2.4 C、平均数是2.4 D、方差是16. 如图,热气球的探测器显示,从热气球A处看一栋楼顶部B处的仰角为30°,看这栋楼底部C处的俯角为60°,热气球A处与楼的水平距离为 ,则这栋楼的高度为( )
A、 B、 C、 D、5. 在体育中考训练中,男生小杰6次立定跳远的成绩(单位:米)如下:2.4,2.3,2.6,2.4,2.2,2.5,关于这组数据,下列结论不正确的是( )A、众数是2.4 B、中位数是2.4 C、平均数是2.4 D、方差是16. 如图,热气球的探测器显示,从热气球A处看一栋楼顶部B处的仰角为30°,看这栋楼底部C处的俯角为60°,热气球A处与楼的水平距离为 ,则这栋楼的高度为( )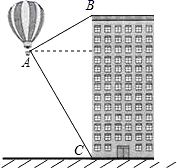 A、 B、 C、 D、7. 如图,是一个容器的三视图,向该容器中匀速注水,下面哪一个图象可以大致刻画容器中水的高度h与时间t的函数关系( )
A、 B、 C、 D、7. 如图,是一个容器的三视图,向该容器中匀速注水,下面哪一个图象可以大致刻画容器中水的高度h与时间t的函数关系( ) A、
A、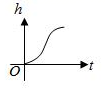 B、
B、 C、
C、 D、
D、 8. 对于 这类特殊的三次方程可以这样来解.先将方程的左边分解因式: ,这样原方程就可变为 ,即有 或 ,因此,方程 和 的所有解就是原方程的解.据此,显然 有一个解为 ,设它的另两个解为 , ,则式子 的值( )A、 B、1 C、 D、79. 如图,抛物线 ( )经过点 ,对称轴为直线 .下列结论:① ;② ;③对于任意实数m,总有 ;④对于a的每一个确定值,若一元二次方程 (P为常数,且 )的根为整数,则P的值有且只有三个,其中正确的结论是( )
8. 对于 这类特殊的三次方程可以这样来解.先将方程的左边分解因式: ,这样原方程就可变为 ,即有 或 ,因此,方程 和 的所有解就是原方程的解.据此,显然 有一个解为 ,设它的另两个解为 , ,则式子 的值( )A、 B、1 C、 D、79. 如图,抛物线 ( )经过点 ,对称轴为直线 .下列结论:① ;② ;③对于任意实数m,总有 ;④对于a的每一个确定值,若一元二次方程 (P为常数,且 )的根为整数,则P的值有且只有三个,其中正确的结论是( )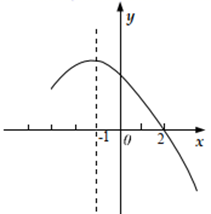 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
10. 计算: .11. 不等式组 的非负整数解是.12. 如图,在 中, , , ,将 绕点A逆时针旋转得到 ,使点 落在 边上,连接 ,则 的长度是 .
 13. 如图,点O是 的重心,延长 交 于点D,延长 交 于点E,过点O作 交 于点F.现随机向 内部抛一米粒,则米粒落在图中阴影部分的概率为.
13. 如图,点O是 的重心,延长 交 于点D,延长 交 于点E,过点O作 交 于点F.现随机向 内部抛一米粒,则米粒落在图中阴影部分的概率为. 14. 我国古代数学家杨辉发现了如图所示的三角形,我们称之为“杨辉三角”,它具有一定的规律性.从图中取一斜列数:1,3,6,10,15,…,我们把第一个数记为 ,第二个数记为 ,第三个数记为 ,…,第n个数记为 . ,则n的值为.
14. 我国古代数学家杨辉发现了如图所示的三角形,我们称之为“杨辉三角”,它具有一定的规律性.从图中取一斜列数:1,3,6,10,15,…,我们把第一个数记为 ,第二个数记为 ,第三个数记为 ,…,第n个数记为 . ,则n的值为.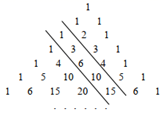 15. 如图,在 中, , , , 是 上方一动点,且 , 交 于点E.当点P运动到 时, 的值为;随着点P的运动, 的最大值为.
15. 如图,在 中, , , , 是 上方一动点,且 , 交 于点E.当点P运动到 时, 的值为;随着点P的运动, 的最大值为.
三、解答题
-
16. 先化简,再求值: ,其中 .17. 如图,在 中, 是 边上的中线,E是 边上一点,过点 作 交 的延长线于点F.
 (1)、求证: .(2)、当 , , 时,求 的长.18. 如图,一次函数 的图象与反比例函数 的图象在第三象限交于点 ,与y轴的正半轴交于点B,且 .
(1)、求证: .(2)、当 , , 时,求 的长.18. 如图,一次函数 的图象与反比例函数 的图象在第三象限交于点 ,与y轴的正半轴交于点B,且 .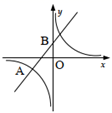 (1)、求函数 和 的解析式;(2)、将直线 向下平移4个单位后得到直线 : ( ),l与反比例函数 的图象相交,求使 成立的x的取值范围.19. 为了解“永远跟党走”主题宣传教育活动的效果,某校组织了党史知识问卷测试,从中抽取部分答卷,统计整理得到如下不完整的频数分布表和扇形统计图.
(1)、求函数 和 的解析式;(2)、将直线 向下平移4个单位后得到直线 : ( ),l与反比例函数 的图象相交,求使 成立的x的取值范围.19. 为了解“永远跟党走”主题宣传教育活动的效果,某校组织了党史知识问卷测试,从中抽取部分答卷,统计整理得到如下不完整的频数分布表和扇形统计图.等级
成绩/分
频数
A
B
8
C
D
4

根据以上信息,解答下列问题:
(1)、填空: , , 形统计图中“D”等级的圆心角为度;(2)、若成绩不低于90分为优秀,请估计该校2000名学生中达到优秀等级的人数;(3)、已知A等级中有2名男生,现从A等级中随机抽取2名同学,试用列表或树状图的方法求出恰好抽到一男一女的概率.20. 如图, , 切 分别于点B,C, 交 于点D,连接 并延长交 于点E. (1)、求证: ;(2)、若 的半径为13, ,求 的长.21. 某公园有一个截面由抛物线和长方形构成的观景拱桥,如图所示,长方形的长为16米,宽为3米,抛物线的最高处C距地面7米.
(1)、求证: ;(2)、若 的半径为13, ,求 的长.21. 某公园有一个截面由抛物线和长方形构成的观景拱桥,如图所示,长方形的长为16米,宽为3米,抛物线的最高处C距地面7米. (1)、经过讨论,同学们得出如图所示的三种建立平面直角坐标系的方案,请从中选择一种求出抛物线的表达式;
(1)、经过讨论,同学们得出如图所示的三种建立平面直角坐标系的方案,请从中选择一种求出抛物线的表达式;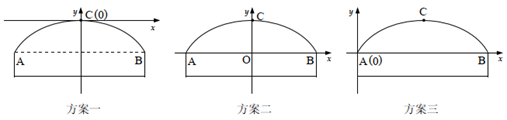 (2)、观景拱桥下有两根长为4.75米的对称安置的立柱,求这两根立柱的水平距离;(3)、现公园管理处打算,在观景拱桥的下方限高3.5米水平线上,两立柱间安装一个长8米的矩形广告牌 ,为安全起见,要求广告牌的最高处与拱桥的桥面之间的距离 不得小于0.35米,求矩形广告牌的最大高度 .22. 在一个三角形中,如果有两个内角 与 满足 ,那么我们称这样的三角形为“亚直角三角形”.根据这个定义,显然 ,则这个三角形的第三个角为 ,这就是说“亚直角三角形”是特殊的钝角三角形.
(2)、观景拱桥下有两根长为4.75米的对称安置的立柱,求这两根立柱的水平距离;(3)、现公园管理处打算,在观景拱桥的下方限高3.5米水平线上,两立柱间安装一个长8米的矩形广告牌 ,为安全起见,要求广告牌的最高处与拱桥的桥面之间的距离 不得小于0.35米,求矩形广告牌的最大高度 .22. 在一个三角形中,如果有两个内角 与 满足 ,那么我们称这样的三角形为“亚直角三角形”.根据这个定义,显然 ,则这个三角形的第三个角为 ,这就是说“亚直角三角形”是特殊的钝角三角形.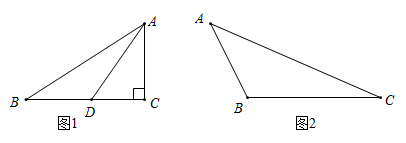 (1)、若某三角形是“亚直角三角形”,且一个内角为100°,请直接写出它的两个锐角的度数;(2)、如图1,在 中, , , ,点D在边 上,连接 ,且 不平分 .若 是“亚直角三角形”,求线段 的长;(3)、如图2,在钝角 中, , , , 的面积为42,求证: 是“亚直角三角形”.23. 如图1,已知抛物线 与x轴正半轴交于点A, 为x轴上另一点,直线 交抛物线的对称轴于点C,过点B作 交过点C平行于x轴的直线于点M,D为抛物线的顶点.
(1)、若某三角形是“亚直角三角形”,且一个内角为100°,请直接写出它的两个锐角的度数;(2)、如图1,在 中, , , ,点D在边 上,连接 ,且 不平分 .若 是“亚直角三角形”,求线段 的长;(3)、如图2,在钝角 中, , , , 的面积为42,求证: 是“亚直角三角形”.23. 如图1,已知抛物线 与x轴正半轴交于点A, 为x轴上另一点,直线 交抛物线的对称轴于点C,过点B作 交过点C平行于x轴的直线于点M,D为抛物线的顶点. (1)、直接用含m的代数式表示点A,D的坐标;(2)、若点M恰好在该抛物线上,求四边形 的面积;(3)、如图2,在(2)的条件下,连接 ,G为x轴上一点,H为抛物线上一动点,若以点A,G,H为顶点的三角形与 相似,请直接写出点H及其对应的点G的坐标.
(1)、直接用含m的代数式表示点A,D的坐标;(2)、若点M恰好在该抛物线上,求四边形 的面积;(3)、如图2,在(2)的条件下,连接 ,G为x轴上一点,H为抛物线上一动点,若以点A,G,H为顶点的三角形与 相似,请直接写出点H及其对应的点G的坐标.