河南省新蔡县2021年数学中考一模试卷

试卷更新日期：2021-06-24 类型：中考模拟

进入出卷网下载

一、单选题

1. 在实数 $- 1$ ， $- \sqrt{2}$ ，0， $\frac{1}{4}$ 中，最小的实数是（）．

A、 $- 1$ B、 $\frac{1}{4}$ C、0 D、 $- \sqrt{2}$

查看试题解析
2. 如图， $⊙ O$ 的直径 $C D$ 为26，弦 $A B$ 的长为24，且 $A B ⊥ C D$ ，垂足为M，则 $C M$ 的长为（）

A、25 B、8 C、5 D、13

查看试题解析
3. 小明在一次训练中，掷出的实心球飞行高度y（米）与水平距离x（米）之间的关系大致满足二次函数 $y = - \frac{1}{12} x^{2} + \frac{2}{3} x + \frac{5}{3}$ ，则小明此次成绩为（）

A、8米 B、10米 C、12米 D、14米

查看试题解析
4. 如图，点 $C (4 ， 0)$ ， $D (0 ， 3)$ ， $O (0 ， 0)$ ，在 $⊙ A$ 上， $B D$ 是 $⊙ A$ 的一条弦，则 $\sin ∠ O B D =$ （）.

A、 $\frac{1}{2}$ B、 $\frac{3}{4}$ C、 $\frac{4}{5}$ D、 $\frac{3}{5}$

查看试题解析
5. 设 $A (2 ， y_{1})$ ， $B (3 ， y_{2})$ ， $C (- 4 ， y_{3})$ 是抛物线 $y = 3 {(x - 1)}^{2} + k$ 图象上的三点，则 $y_{1}$ ， $y_{2}$ ， $y_{3}$ 的大小关系为（）

A、 $y_{3} > y_{2} > y_{1}$ B、 $y_{3} > y_{1} > y_{2}$ C、 $y_{2} > y_{1} > y_{3}$ D、 $y_{1} > y_{3} > y_{2}$

查看试题解析
6. 如图， $B D$ 是 $⊙ O$ 的直径，点A，C在 $⊙ O$ 上， $\overset{⌢}{A B} = \overset{⌢}{A D}$ ， $A C$ 交 $B D$ 于点G．若 $∠ C O D = 126 °$ ．则 $∠ A G B$ 的度数为（）

A、 $99 °$ B、 $108 °$ C、 $110 °$ D、 $117 °$

查看试题解析
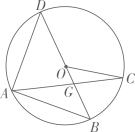7. 从1、2、3、4四个数中随机选取两个不同的数，分别记为a、c ，则关于x的一元二次方程ax²＋4x＋c＝0有实数解的概率为（）

A、 $\frac{1}{4}$ B、 $\frac{1}{3}$ C、 $\frac{1}{2}$ D、 $\frac{2}{3}$

查看试题解析
8. 如图，反比例函数 $y = \frac{k}{x} (x < 0)$ 与一次函数 $y = x + 4$ 的图象交于 $A ， B$ 两点， $A ， B$ 两点的横坐标分别为 $- 3 ， - 1$ .则关于x的不等式 $\frac{k}{x} < x + 4 (x < 0)$ 的解集为（）

A、 $x < - 3$ B、 $- 3 < x < - 1$ C、 $- 1 < x < 0$ D、 $x < - 3$ 或 $- 1 < x < 0$

查看试题解析
9. 如图所示，已知二次函数 $y = a x^{2} + b x + c$ 的图象与 $x$ 轴交于 $A ， B$ 两点，与 $y$ 轴交于点 $C$ ， $O A = O C$ ，对称轴为直线 $x = 1$ ，则下列结论：① $a b c < 0$ ；② $a + \frac{1}{2} b + \frac{1}{4} c = 0$ ；③ $a c - b + 1 = 0$ ；④ $2 + c$ 是关于 $x$ 的一元二次方程 $a x^{2} + b x + c = 0$ 的一个根.其中正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
10. 如图甲所示，A，B是半径为2的⊙O上两点，且OA⊥OB，点P从点A出发，在⊙O以每秒一个单位长度度速度匀速运动，回到点A运动结束，设P点的运动时间为x（单位：s），弦BP的长为y，那么在图乙中可能表示y与x函数关系的是（）

A、① B、② C、②或④ D、①或③

查看试题解析

二、填空题

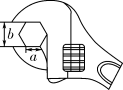
11. 使 $\frac{\sqrt{3 - x}}{x}$ 在实数范围内有意义，则实数x的取值范围是.

查看试题解析
12. 如图，工人师傅用扳手拧形状为正六边形的螺帽，现测得扳手的开口宽度 $b = 3cm$ ，则螺帽边长 $a =$ cm.

查看试题解析
13. 某商品进货单价为30元，按40元一个销售能卖40个；若销售单价每涨1元，则销量减少1个．为了获得最大利润，此商品的最佳售价应为元．

查看试题解析
14. 如图，等边三角形 $A B C$ 的边长为2，以 $A$ 为圆心，1为半径作圆分别交 $A B ， A C$ 边于 $D ， E$ ，再以点 $C$ 为圆心， $C D$ 长为半径作圆交 $B C$ 边于 $F$ ，连接 $E ， F$ ，那么图中阴影部分的面积为.

查看试题解析
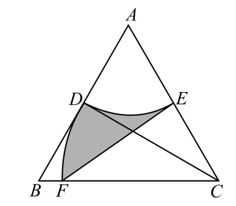15. 如图，在矩形纸片 $A B C D$ 中， $A B = 4$ ， $B C = 4 \sqrt{2}$ ，点E是 $A B$ 的中点，点F是 $A D$ 边上的一个动点，将 $△ A E F$ 沿 $E F$ 所在直线翻折，得到 $△ A' E F$ ，连接 $A' C$ ， $A' D$ ，则当 $△ A' D C$ 是以 $A' D$ 为腰的等腰三角形时， $F D$ 的长是.

查看试题解析

三、解答题

16. 先化简，再求值： $\frac{x^{2} - 2 x + 1}{2 x + 4} \div (x - \frac{1 + 2 x}{x + 2})$ ，其中x的值从不等式组 ${\begin{array}{l} - x \leq 2 \\ \frac{3}{2} x - 1 < 2 \end{array}$ 的整数解中选取.

查看试题解析
17. 某品牌牛奶供应商提供A、B、C、D四种不同口味的牛奶供学生饮用，学校为了了解学生对不同口味的牛奶的喜好，对全校订牛奶的学生进行了随机调查，并根据调查结果绘制了如图所示的两幅不完整的统计图，根据统计图的信息解决下列问题：

(1)、本次调查的学生有多少人？

(2)、补全上面的条形统计图；

(3)、扇形统计图中C对应的圆心角度数是；

(4)、若该校有400名学生订了该品牌的牛奶，每名学生每天只订一盒牛奶，要使学生能喝到自己喜欢的牛奶，则该牛奶供应商送往该校的牛奶中，A、B口味的牛奶共约多少盒？

查看试题解析
18. 在平面直角坐标系中，二次函数y＝ax²+bx+3的图象经过点A（3，0）和点B（4，3）.

(1)、求二次函数的表达式

(2)、求二次函数图象的顶点坐标和对称轴.

查看试题解析
19. 如图，已知AB为⊙O的直径，点E在⊙O上，∠EAB的平分线交⊙O于点C，过点C作AE的垂线，垂足为D，直线DC与AB的延长线交于点P．

(1)、判断直线PC与⊙O的位置关系，并说明理由；

(2)、若tan∠P= $\frac{3}{4}$ ，AD=6，求线段AE的长．

查看试题解析
20. 某数学兴趣小组学过锐角三角函数后，计划测量中原福塔的总高度.如图所示，在B处测得福塔主体建筑顶点A的仰角为45°，福塔顶部桅杆天线AD高120m，再沿CB方向前进20m到达E处，测得桅杆天线顶部D的仰角为53.4°.求中原福塔CD的总高度.（结果精确到1m.参考数据：sin53.4°≈0.803，cos53.4°≈0.596，tan53.4°≈1.346）

查看试题解析
21. 某药店出售普通口罩和N95口罩.如表为两次销售记录：

普通口罩/个

N95口罩/个

总销售额/元

500

400

5000

600

300

4200

(1)、求普通口罩和N95口罩的销售单价分别是多少？

(2)、该药店计划再次购进1000个口罩，根据市场实际需求，普通口罩的数量不低于N95口罩数量的4倍.已知普通口罩的进价为1元/个，N95口罩的进价为6元/个.为使该药店售完这1000个口罩后的总利润最大，该药店应如何进货？并求出最大利润.

查看试题解析
22. 古希腊数学家毕达哥拉斯认为：“一切平面图形中最美的是圆”.请研究如下美丽的圆.如图，线段AB是⊙O的直径，延长AB至点C，使BC＝OB，点E是线段OB的中点，DE⊥AB交⊙O于点D，点P是⊙O上一动点（不与点A，B重合），连接CD，PE，PC.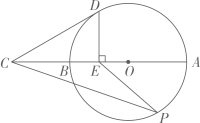

(1)、求证：CD是⊙O的切线；

(2)、小明在研究的过程中发现 $\frac{P E}{P C}$ 是一个确定的值.回答这个确定的值是多少？并对小明发现的结论加以证明.

查看试题解析
23. 如图，已知抛物线 $y = a x^{2} + b x + 3$ 与x轴交于 $A (- 1 ， 0)$ 、 $B (3 ， 0)$ 两点，与y轴交于点C，连接 $B C$ ，

(1)、求抛物线的解析式；

(2)、若点P为线段 $B C$ 上的一动点（不与B、C重合）， $P M // y$ 轴，且 $P M$ 交抛物线于点M，交x轴于点N，当 $△ B C M$ 的面积最大时，求点P的坐标；

(3)、在（2）的条件下，当 $△ B C M$ 的面积最大时，点D是抛物线的对称轴上的动点，在抛物线上是否存在点E，使得以A、P、D、E为顶点的四边形为平行四边形？若存在，请直接写出点E的坐标；若不存在，请说明理由.

查看试题解析

普通口罩/个	N95口罩/个	总销售额/元
500	400	5000
600	300	4200