海南省海口市2021年九年级下学期数学考联考试卷
试卷更新日期:2021-06-24 类型:中考模拟
一、单选题
-
1. 的绝对值是( )A、 B、 C、 D、20212. 下列运算,正确的是( )A、a3+a3=2a6 B、a2. a5=a10 C、a6÷a2=a4 D、(3ab)2=3a2b23. 化简 的结果是( )A、1 B、-1 C、3 D、-34. 据国家邮政局统计,2021年农历除夕和初一两天,全国快递处理超130 000 000件,与去年同期相比增长223%,快递的春节“不打烊”服务确保了广大用户能够顺利收到年货,欢度佳节.将130 000 000用科学记数法表示应为( )A、1.3×107 B、13×107 C、1.3×108 D、0.13×1095. 一组数据2,﹣1,0,2,﹣3,3的中位数和众数分别是( )A、1,2 B、1,3 C、﹣1,2 D、0,26. 若反比例函数 的图象经过点(2,1),则它的图象也一定经过的点是( )A、(-1,-2) B、(2,-1) C、(1,-2) D、(-2,1)7. 已知x-2y=-1,则代数式1+4y-2x的值是( )A、-3 B、-1 C、2 D、38. 不等式组 的整数解有( )A、3个 B、4个 C、5个 D、6个9. 一副三角板如图方式摆放,点D在直线EF上,且AB//EF,则∠ADE的度数是( )
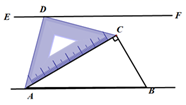 A、105° B、75° C、60° D、45°10. 图2是图1中长方体的三视图,若用S表示面积, , ,则 ( )
A、105° B、75° C、60° D、45°10. 图2是图1中长方体的三视图,若用S表示面积, , ,则 ( )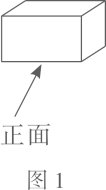
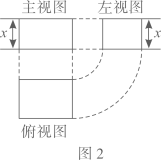 A、 B、 C、 D、11. 如图,在正方形 中, ,点 , 分别在边 , 上, .若将四边形 沿 折叠,点 恰好落在 边上,则 的长度为( )
A、 B、 C、 D、11. 如图,在正方形 中, ,点 , 分别在边 , 上, .若将四边形 沿 折叠,点 恰好落在 边上,则 的长度为( ) A、1 B、 C、 D、212. 如图,在 中,AB=AC,分别以点A、B为圆心,以适当的长为半径作弧,两弧分别交于E,F,作直线EF,D为BC的中点,M为直线EF上任意一点.若BC=4, 面积为10,则BM+MD长度的最小值为( )
A、1 B、 C、 D、212. 如图,在 中,AB=AC,分别以点A、B为圆心,以适当的长为半径作弧,两弧分别交于E,F,作直线EF,D为BC的中点,M为直线EF上任意一点.若BC=4, 面积为10,则BM+MD长度的最小值为( ) A、 B、3 C、4 D、5
A、 B、3 C、4 D、5二、填空题
-
13. 点(1,y1)、(2,y2)是直线 y =2x+1上的两点,则y1 y2(填“>” 或“ =”或 “<”).14. 如图,AB为⊙O的直径,PD切⊙O于点C,交BA的延长线于点D,且CD=CO,则∠PCB等于.
 15. 如图,在Rt△ABC中,∠ACB=90°,点P以每秒1cm的速度从点A出发,沿折线AC→CB运动,到点B停止. 过点P作PD⊥AB于点D,PD的长y(cm)与点P的运动时间x(秒)的函数图象所示. 当点P运动6秒时,PD的长是.
15. 如图,在Rt△ABC中,∠ACB=90°,点P以每秒1cm的速度从点A出发,沿折线AC→CB运动,到点B停止. 过点P作PD⊥AB于点D,PD的长y(cm)与点P的运动时间x(秒)的函数图象所示. 当点P运动6秒时,PD的长是. 16. 如图,在平面直角坐标系中,第一次将 变换成 ,第二次将 变换成 ,第三次将 变换成 , ,将 进行n次变换,得到 ,观察每次变换中三角形顶点坐标有何变化,找出规律,推测 的坐标是 , 的坐标是.
16. 如图,在平面直角坐标系中,第一次将 变换成 ,第二次将 变换成 ,第三次将 变换成 , ,将 进行n次变换,得到 ,观察每次变换中三角形顶点坐标有何变化,找出规律,推测 的坐标是 , 的坐标是.
三、解答题
-
17.(1)、计算: ;(2)、化简:18. 某大型超市投入15000元资金购进 、 两种品牌的矿泉水共600箱,矿泉水的成本价和销售价如下表所示:
类别/单价
成本价(元/箱)
销售价(元/箱)
A品牌
20
32
B品牌
35
50
(1)、该大型超市购进 、 品牌矿泉水各多少箱?(2)、全部销售完600箱矿泉水,该超市共获得多少利润?19. 近日,据农业农村部消息,“红火蚁”已传播至我国12个省份,435个县市区,经常出现在路边、草地、公园……其危害性极大.国家九部门联合部署防控行动,紧急防控红火蚁.某公司为了解员工对防护措施的了解程度(包括不了解、了解很少、基本了解和很了解),通过网上问卷调查的方式进行了随机抽样调查(每名员工必须且只能选择一项),并将调查结果绘制成如下两幅统计图.
请你根据上面的信息,解答下列问题
(1)、本次共调查了名员工,条形统计图中m=;(2)、若该公司共有员工1000名,请你估计不了解防护措施的人数=名;(3)、在调查中,发现有4名员工对防护措施很了解,其中有3名男员工、1名女员工.若从他们中随机抽取2名,让其在公司群内普及防护措施,求恰好抽中一男一女的概率.
20. 为了丰富学生社会实践活动,学校组织学生到红色文化基地A和人工智能科技馆C参观学习.如图,学校在点B处,A位于学校的东北方向,C位于学校南偏东30°方向,C在A的南偏西15°方向(30+30 )km处.学生分成两组,第一组前往A地,第二组前往C地,两组同学同时从学校出发,第一组乘客车,速度是40km/h,第二组乘公交车,速度是30km/h.(结果保留根号) (1)、求出∠BAC的度数和BC的长;(2)、请问,哪组同学先到达目的地?请说明理由.21. 如图,菱形ABCD中,AB=4 ,连接BD,点P是线段BC上一动点(不与点B重合),AP与对角线BD交于点E,连接EC.
(1)、求出∠BAC的度数和BC的长;(2)、请问,哪组同学先到达目的地?请说明理由.21. 如图,菱形ABCD中,AB=4 ,连接BD,点P是线段BC上一动点(不与点B重合),AP与对角线BD交于点E,连接EC. (1)、求证:△ABE ≌ △CBE;(2)、如图①,若∠ABC=60°,BP= ,求BE的长;(3)、若AB=AC,如图②,点P、N分别从点B、C同时出发,以相同速度沿BC、CA向终点C和A运动,连接AP和BN交于点G,当tan∠CBN= 时,求BG与GN的比值.22. 如图1,在平面直角坐标系中,抛物线y=ax2+bx+3交x轴于A,B两点,点A,B的坐标分别为(﹣3,0),(1,0),与y轴交于点C,点D为顶点.
(1)、求证:△ABE ≌ △CBE;(2)、如图①,若∠ABC=60°,BP= ,求BE的长;(3)、若AB=AC,如图②,点P、N分别从点B、C同时出发,以相同速度沿BC、CA向终点C和A运动,连接AP和BN交于点G,当tan∠CBN= 时,求BG与GN的比值.22. 如图1,在平面直角坐标系中,抛物线y=ax2+bx+3交x轴于A,B两点,点A,B的坐标分别为(﹣3,0),(1,0),与y轴交于点C,点D为顶点. (1)、求该抛物线的表达式;(2)、点E是直线AC下方的抛物线上一点,且S△ACE=2S△ACD , 求点E的坐标;(3)、如图2,若点P是线段AC上的一个动点,∠DPQ=∠DAC,DP⊥DQ,则点P在线段AC上运动时,D点不变,Q点随之运动.求当点P从点A运动到点C时,点Q运动的路径长.
(1)、求该抛物线的表达式;(2)、点E是直线AC下方的抛物线上一点,且S△ACE=2S△ACD , 求点E的坐标;(3)、如图2,若点P是线段AC上的一个动点,∠DPQ=∠DAC,DP⊥DQ,则点P在线段AC上运动时,D点不变,Q点随之运动.求当点P从点A运动到点C时,点Q运动的路径长.