贵州省黔东南州2021年数学中考模拟试卷（二）

试卷更新日期：2021-06-24 类型：中考模拟

进入出卷网下载

一、单选题

1. $| - 2021 | =$ （）

A、2021 B、-2021 C、 $\frac{1}{2021}$ D、 $- \frac{1}{2021}$

查看试题解析
2. 如图，是由棱长都相等的四个小正方体组成的几何体.该几何体的主视图是（）

A、 B、 C、 D、

查看试题解析
3. 为深入贯彻习近平总书记关于决战决胜脱贫攻坚重要指导精神，全力以赴推进东西部扶贫劳务协作工作，助力打赢脱贫攻坚战，9月17日，“浙江—贵州”2020年东西部劳务协作专场招聘会在黔东南州凯里市举办，来自浙江省39家企业现场招聘，提供7400个就业岗位.请用科学记数法表示7400这个数字（）

A、 $0.74 \times 10^{4}$ B、 $7.4 \times 10^{3}$ C、 $7.4 \times 10^{2}$ D、 $74 \times 10^{2}$

查看试题解析
4. 下列运算中，计算正确的是（）

A、 ${(a^{2} b)}^{4} = a^{6} b^{4}$ B、 ${(3 a^{2})}^{3} = 27 a^{6}$ C、 $a^{6} \div a^{2} = a^{3}$ D、 $a^{6} \cdot a^{2} = a^{12}$

查看试题解析
5. 下列图形中既是中心对称图形又是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
6. 设m、n是方程 $x^{2} + x - 2021 = 0$ 的两个实数根，则 $m^{2} + 2 m + n$ 的值为（）

A、2018 B、2019 C、2020 D、2021

查看试题解析
7. 如图，在 $R t △ A B C$ 中， $∠ C = 90 °$ ， $A D$ 平分 $∠ C A B$ ， $D E ⊥ A B$ 于E，则下列结论中，不正确的是（）

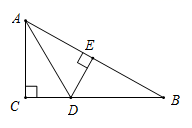A、 $D E$ 平分 $∠ A D B$ B、 $B D + E D = B C$ C、 $A D$ 平分 $∠ E D C$ D、 $E D + A C > A D$

查看试题解析
8. 如图，在平面直角坐标系中，菱形ABCD的顶点A，B在反比例函数 $y = \frac{k}{x}$ （ $k > 0$ ， $x > 0$ ）的图象上，横坐标分别为1，4，对角线 $B D ∥ x$ 轴.若菱形ABCD的面积为 $\frac{45}{2}$ ，则k的值为（）

A、 $\frac{5}{4}$ B、 $\frac{15}{4}$ C、4 D、5

查看试题解析
9. 2020年在抗击“新型冠状病毒”期间，甲、乙两人准备帮助某抗疫指挥中心整理一批新到的物资，甲单独整理需要40分钟完工；若甲、乙共同整理20分钟后，乙需再单独整理30分钟才能完工.设乙单独整理这批物资需要x分钟完工，则根据题意列得方程（）

A、 $\frac{20}{40} + \frac{20}{x} = 1$ B、 $\frac{20}{40} + \frac{20 + 30}{x} = 1$ C、 $\frac{20}{40} + \frac{30}{x} = 1$ D、 $\frac{20 + 30}{40} + \frac{30}{x} = 1$

查看试题解析
10. 如图，抛物线 $y = a x^{2} + b x + c$ 过点 $(- 1 ， 0)$ ，且对称轴为直线 $x = 1$ ，有下列结论：① $a b c < 0$ ；② $10 a + 3 b + c > 0$ ；③抛物线经过点 $(4 ， y_{1})$ 与点 $(- 3 ， y_{2})$ ，则 $y_{1} > y_{2}$ ；④无论a，b，c取何值，抛物线都经过同一个点 $(- \frac{c}{a} ， 0)$ ；⑤ $a m^{2} + b m + a \geq 0$ ，其中所有正确的结论是（）

A、①②③④⑤ B、③④⑤ C、②③④⑤ D、②④⑤

查看试题解析

二、填空题

11. 在二次根式 $\sqrt{2 x + 4}$ 中，x的取值范围是．

查看试题解析
12. 一组数据：12，12，14，11，16，15则这组数据的中位数是.

查看试题解析
13. 分解因式： $2 a^{2} - 8 b^{2}$ .

查看试题解析
14. 如图，将长方形纸片 $A B C D$ 沿对角线 $B D$ 折叠，若 $A B = 4 cm$ ， $A E = 3 cm$ ，则重叠部分（即 $△ B D E$ ）的面积是.

查看试题解析
15. 一个不透明的布袋内装有除颜色外，其余完全相同的3个红球，2个白球，1个黄球，搅匀后，从中随机摸出一个球，记下颜色后放回搅匀，再从中随机摸出一个球，则两次都摸到红球的概率为.

查看试题解析
16. 如图， $∠ C A D + ∠ B + ∠ C + ∠ D + ∠ E =$ .

查看试题解析
17. 在 $△ A B C$ 中， ${(\sqrt{3} \tan A - 3)}^{2} + | 2 \cos B - \sqrt{3} | = 0$ ，则 $△ A B C$ 为三角形.

查看试题解析
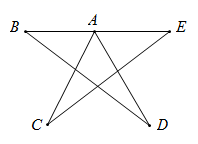18. 已知等腰三角形的两边长分别为4cm和6cm，则这个等腰三角形的周长为cm

查看试题解析
19. 如图，正方形ABCD内接于⊙O，⊙O的半径为2，以点A为圆心，以AC为半径画弧交AB的延长线于点E，交AD的延长线于点F，则图中阴影部分的面积是.

查看试题解析
20. 观察下列等式：
${1.4}^{2} - 1^{2} = 3 \times 5$ ；

${2.5}^{2} - 2^{2} = 3 \times 7$ ；

${3.6}^{2} - 3^{2} = 3 \times 9$

${4.7}^{2} - 4^{2} = 3 \times 11$ ；

…………

则第 $n$ （ $n$ 是正整数）个等式为.

查看试题解析

三、解答题

21.

(1)、计算： $| 1 - \sqrt{2} | + {(\sqrt{3} + 1)}^{0} - 4 \sin 30 ° + {(- 1)}^{2021} + {(\frac{1}{2})}^{- 1}$

(2)、先化简，再求值： $\frac{m^{2} + 6 m + 9}{m - 1} \div (\frac{4}{m - 1} + 1)$ ，其中 $m = \sqrt{2} - 2$ .

查看试题解析

22. 某中学1000名学生参加了”环保知识竞赛“，为了了解本次竞赛成绩情况，从中抽取了部分学生的成绩（得分取整数，满分为100分）作为样本进行统计，并制作了如图频数分布表和频数分布直方图（不完整且局部污损，其中“■”表示被污损的数据）.请解答下列问题：

成绩分组	频数	频率
50≤x＜60	8	0.16
60≤x＜70	12	a
70≤x＜80	■	0.5
80≤x＜90	3	0.06
90≤x≤100	b	c
合计	■	1

(1)、写出a，b，c的值；

(2)、请估计这1000名学生中有多少人的竞赛成绩不低于70分；

(3)、在选取的样本中，从竞赛成绩是80分以上（含80分）的同学中随机抽取两名同学参加环保知识宣传活动，求所抽取的2名同学来自同一组的概率.

查看试题解析

23. 如图，AB、AC分别是⊙O的直径和弦，OD⊥AC于点D．过点A作⊙O的切线与
OD的延长线交于点P，PC、AB的延长线交于点F．

(1)、求证：PC是⊙O的切线；

(2)、若∠ABC=60°，AB=10，求线段CF的长．

查看试题解析
24. 为迎接“七·一”党的生日，某校准备组织师生共310人参加一次大型公益活动，租用4辆大客车和6辆小客车恰好全部坐满，已知每辆大客车的座位数比小客车多15个.

(1)、求每辆大客车和小客车的座位数；

(2)、经学校统计，实际参加活动人数增加了40人，学校决定调整租车方案，在保持租用车辆总数不变的情况下，为使所有参加活动的师生均有座位，最多租用小客车多少辆？

查看试题解析
25. 阅读材料：
材料一：数学上有一种根号内又带根号的数，它们能通过完全平方式及二次根式的性质化去一层(或多层)根号，如： $\sqrt{{(\sqrt{1})}^{2} + {(\sqrt{2})}^{2} - 2 \times \sqrt{1} \times \sqrt{2}} = \sqrt{{(\sqrt{1} - \sqrt{2})}^{2}} = | \sqrt{1} - \sqrt{2} | = \sqrt{2} - 1$

材料二：配方法是初中数学思想方法中的一种重要的解题方法，配方法的最终目的就是配成完全平方式，利用完全平方式来解决问题，它的应用非常广泛，在解方程、化简根式、因式分解等方面都经常用到.

如： $x^{2} + 2 \sqrt{2} x + 3 = x^{2} + 2 \cdot \sqrt{2} \cdot x + {(\sqrt{2})}^{2} + 1 = {(x + \sqrt{2})}^{2} + 1$

∵ ${(x + \sqrt{2})}^{2} \geq 0$ ，∴ ${(x + \sqrt{2})}^{2} + 1 \geq 1$ ，即 $x^{2} + 2 \sqrt{2} x + 3 \geq 1$

∴ $x^{2} + 2 \sqrt{2} x + 3$ 的最小值为 $1$

阅读上述材料解决下面问题：

(1)、 $\sqrt{4 - 2 \sqrt{3}} =$ ， $\sqrt{5 + 2 \sqrt{6}} =$ ；

(2)、求 $x^{2} + 4 \sqrt{3} x + 11$ 的最值；

(3)、已知 $x = \sqrt{3 - \sqrt{13 - 4 \sqrt{3}}}$ ，求 $- \frac{1}{4} (4 + 2 \sqrt{3}) x^{2} y^{2} + (\sqrt{3} + 1) x y - 5$ 的最值.

查看试题解析
26. 如图，已知二次函数y=ax²+bx+c的图象与x轴相交于A（﹣1，0），B（3，0）两点，与y轴相交于点C（0，﹣3）．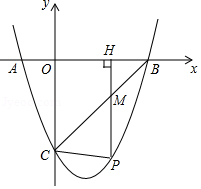

(1)、求这个二次函数的表达式；

(2)、若P是第四象限内这个二次函数的图象上任意一点，PH⊥x轴于点H，与BC交于点M，连接PC．
①求线段PM的最大值；
②当△PCM是以PM为一腰的等腰三角形时，求点P的坐标．

查看试题解析