广西柳州市2021年数学中考模拟试卷
试卷更新日期：2021-06-24 类型：中考模拟
一、单选题
-
1. ﹣3的绝对值是（ ）A、﹣3 B、3 C、- D、2. 小友家阳台上有一个如图所示的移动台阶，它的主视图是（ ）
A、
B、
C、
D、
3. 如图是我国几家银行的标志，其中既是轴对称图形又是中心对称图形的是（ ）A、
B、
C、
D、
4. 已知正比例函数y=mx的图象过第一、三象限，则m的取值范围是（ ）A、m<0 B、m≤0 C、m≥0 D、m>05. 计算（﹣2x2y3）•3xy2结果正确的是（ ）A、﹣6x2y6 B、﹣6x3y5 C、﹣5x3y5 D、﹣24x7y56. 正八边形的每个内角的度数是（ ）A、144° B、140° C、135° D、120°7. 如图所示，有6张写有数字的卡片，它们的背面都相同，现将它们背面朝上，从中任取一张是数字3的概率是（ ）
A、 B、 C、 D、8. 广西北部湾某中学为了使学生能够更好地进行体育活动，决定修建一个长方体形状的游泳池，其底面周长为100 m，设游泳池的底面长方形的长为x m，要使游泳池的底面面积为400 m2 ， 则可列方程为（ ）A、x（100-x）=400 B、2x（100-2x）=400 C、x（100-2x）=400 D、x（50-x）=4009. 在一次夏令营活动中，小明同学从营地A出发，要到A地的北偏东60°方向的C处，他先沿正东方向走了200 m到达B地，再沿B地北偏东30°方向走，恰好到达目的地C处，那么，由此可知，B，C两地相距（ ）A、200 m B、150 m C、100 m D、250 m10. 如图，圆的两条弦 相交于点E，且弧 =弧 ， ，则 的度数为( )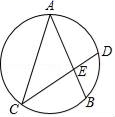
A、 B、 C、 D、11. 如图，在Rt△ABC中，∠ACB=90°，AC=BC，点M在AC边上，且AM=2，MC=6，动点P在AB边上，连接PC，PM，则PC+PM的最小值是 （ ）
A、2 B、8 C、2 D、1012. 如图，E是▱ABCD的边AD的中点，CE与BA的延长线交于点F，若∠FCD=∠D，则下列结论不成立的是（ ）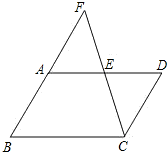
A、AD=CF B、BF=CF C、AF=CD D、DE=EF二、填空题
-
13. 分解因式：x2﹣4x= ．
14. 如图，在△ABC中，P，Q分别为AB，AC的中点.若S△APQ=1，则S四边形PBCQ=.
15. 如图，已知直线a∥b，c⊥d，∠1=36°，则∠2的度数是.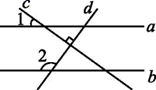
16. 小明同学5次数学单元测试的平均成绩是90分，中位数是91分，众数是94分，则两次最低成绩之和是分.17. 如图，在平面直角坐标系xOy中，函数y＝ （x＞0）的图象经过点A，B，AC⊥x轴于点C，BD⊥y轴于点D，连接OA，OB，则△OAC与△OBD的面积之和为.
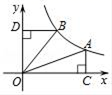18. 一张直角三角形纸片ABC，∠ACB=90°，AB=10，AC=6，点D为BC边上的任一点，沿过点D的直线折叠，使直角顶点C落在斜边AB上的点E处，当△BDE是直角三角形时，则CD的长为.三、解答题
-
19. 计算：20. 已知：如图①，直线l和l外一点P.求作：直线l的垂线，使它经过点P.
作法：如图②，
（ 1 ）在直线l上任取一点A；（2）连接AP，以点P为圆心，AP长为半径作弧，交直线l于点B（点A，B不重合）；（3）连接BP，作∠APB的平分线，交AB于点H，所以直线PH就是所求作的垂线.
根据上面的作法，完成以下问题：
(1)、使用直尺和圆规，补全图形（保留作图痕迹）；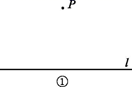
(2)、完成下面的证明.证明：∵PH平分∠APB，
∴∠APH=▲.
∵PA=▲ ，
∴PH⊥直线l于H.（ ）（填推理的依据）
21. 如图，在矩形ABCD中，AB=2，BC=4，对角线AC与BD交于点O，点E在BC边上，DE与AC交于点F，∠CDE=∠ADB.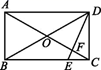
求：
(1)、CE的长；(2)、EF的长.22. 某种子培育基地用A，B，C三种型号的甜玉米种子共1500粒进行发芽试验，从中选出发芽率高的种子进行推广，通过试验知道，C型号种子的发芽率为80%，根据试验数据绘制了下面两个不完整的统计图.
(1)、求C型号种子的发芽数；(2)、通过计算说明，应选哪种型号的种子进行推广?23. 如图，在平面直角坐标系xOy中，直线y=kx+b（k≠0）与x轴交于点A（-2，0），与反比例函数y= （m≠0）的图象交于点B（2，n），连接BO，若S△AOB=4.
(1)、求反比例函数和一次函数的解析式；(2)、若直线AB与y轴的交点为C，求△OCB的面积.24. 某中学为丰富学生的校园生活，准备一次性购买若干个足球和篮球（每个足球的价格相同，每个篮球的价格相同），若购买3个足球和2个篮球共需170元，购买2个足球和5个篮球共需260元.(1)、足球、篮球的单价分别是多少元?(2)、根据该中学的实际情况，需一次性购买足球和篮球共46个，要求购买足球和篮球的总费用不超过1480元，这所中学最多可以购买多少个篮球?25.如图，AB为⊙O的直径，直线CD切⊙O于点D，AM⊥CD于点M，BN⊥CD于N．
(1)、求证：∠ADC=∠ABD；(2)、求证：AD2=AM•AB；(3)、若AM= ， sin∠ABD= ， 求线段BN的长．26. 如图，在平面直角坐标系中，二次函数 的图象与x轴交于A、B两点，B点的坐标为(3，0)，与y轴交于点C（0，－3），点P是直线BC下方抛物线上的一个动点.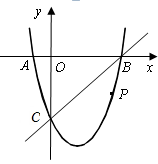
(1)、求二次函数解析式；(2)、连接PO，PC，并将△POC沿y轴对折，得到四边形 .是否存在点P，使四边形 为菱形？若存在，求出此时点P的坐标；若不存在，请说明理由；(3)、当点P运动到什么位置时，四边形ABPC的面积最大？求出此时P点的坐标和四边形ABPC的最大面积.