福建省厦门市集美区2021年九年级初中毕业班适应性综合练习卷数学试卷
试卷更新日期:2021-06-24 类型:中考模拟
一、单选题
-
1. 计算 的结果是( ).A、 B、3 C、 D、2. 下列各组图形中,△ A'B'C'与 △ABC 成中心对称的是( )A、
 B、
B、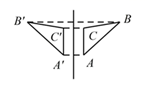 C、
C、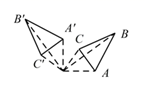 D、
D、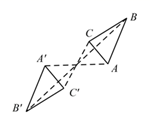 3. 2021年2月25日习近平总书记在全国脱贫攻坚总结表彰大会上庄严宣告:“我国脱贫攻坚战取得了全面胜利,现行标准下9899万农村贫困人口全部脱贫.”用科学记数法表示9899万,其结果是( ).A、 B、 C、 D、4. 一个几何体的侧面展开图如图所示,则该几何体的底面是( )
3. 2021年2月25日习近平总书记在全国脱贫攻坚总结表彰大会上庄严宣告:“我国脱贫攻坚战取得了全面胜利,现行标准下9899万农村贫困人口全部脱贫.”用科学记数法表示9899万,其结果是( ).A、 B、 C、 D、4. 一个几何体的侧面展开图如图所示,则该几何体的底面是( )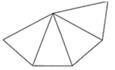 A、
A、 B、
B、 C、
C、 D、
D、 5. 某专卖店专营某品牌的衬衫,店主对上一周中不同尺码的衬衫销售情况统计如下:
5. 某专卖店专营某品牌的衬衫,店主对上一周中不同尺码的衬衫销售情况统计如下:尺码
39
40
41
42
43
平均每天销售数量(件)
10
12
12
20
12
该店主决定本周进货时,增加了一些42码的衬衫,影响该店主决策的统计量是( ).
A、众数 B、方差 C、平均数 D、中位数6. 实数a在数轴上对应的点如图所示,则a、-a、1的大小关系正确的是( )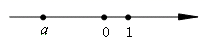 A、-a<a<1 B、a<-a<1 C、1<-a<a D、a<1<-a7. 如图,已知 ∽ ,则下列哪条线段与 的比等于相似比( ).
A、-a<a<1 B、a<-a<1 C、1<-a<a D、a<1<-a7. 如图,已知 ∽ ,则下列哪条线段与 的比等于相似比( ). A、 B、 C、 D、8. 小军到水果店买水果,他身上带的钱恰好可以购买15个苹果或21个橙子,若小军先买了9个苹果,则他身上剩下的钱最多可买橙子( ).A、7个 B、8个 C、9个 D、10个9. 已知二次函数 的图象经过 , , ,且 , , ,则 满足( ).A、 B、 C、 D、10. 公元3世纪,刘徽发现可以用圆内接正多边形的周长近似地表示圆的周长.如图所示,他首先在圆内画一个内接正六边形,再不断地增加正多边形的边数;当边数越多时,正多边形的周长就越接近于圆的周长.刘徽在《九章算术》中写道:“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣.”我们称这种方法为刘徽割圆术,它开启了研究圆周率的新纪元.小牧通过圆内接正 边形,使用刘徽割圆术,得到π的近似值为( )
A、 B、 C、 D、8. 小军到水果店买水果,他身上带的钱恰好可以购买15个苹果或21个橙子,若小军先买了9个苹果,则他身上剩下的钱最多可买橙子( ).A、7个 B、8个 C、9个 D、10个9. 已知二次函数 的图象经过 , , ,且 , , ,则 满足( ).A、 B、 C、 D、10. 公元3世纪,刘徽发现可以用圆内接正多边形的周长近似地表示圆的周长.如图所示,他首先在圆内画一个内接正六边形,再不断地增加正多边形的边数;当边数越多时,正多边形的周长就越接近于圆的周长.刘徽在《九章算术》中写道:“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣.”我们称这种方法为刘徽割圆术,它开启了研究圆周率的新纪元.小牧通过圆内接正 边形,使用刘徽割圆术,得到π的近似值为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
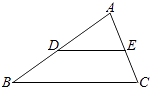
11. 计算: = .12. 如图,在△ABC中,D、E分别是边AB、AC的中点,BC=8,则DE= .
 13. 若点 在一次函数 图象上,且 ,则 的值是.14. 2021年春季各校采取年段错峰用餐,某校为了了解学生在校午餐所需时间,抽取20名学生在校用餐时间,并绘制成频数分布直方图(如图),根据图象信息,预估该校学生平均用餐时间是分钟.
13. 若点 在一次函数 图象上,且 ,则 的值是.14. 2021年春季各校采取年段错峰用餐,某校为了了解学生在校午餐所需时间,抽取20名学生在校用餐时间,并绘制成频数分布直方图(如图),根据图象信息,预估该校学生平均用餐时间是分钟.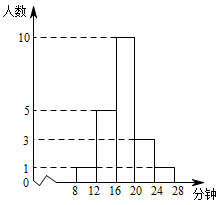 15. 如图,在 中, , .以点B为圆心, 为半径作弧,交 的延长线于点E,线段 沿 方向平移至 .若四边形 的面积为 ,则阴影部分面积为.
15. 如图,在 中, , .以点B为圆心, 为半径作弧,交 的延长线于点E,线段 沿 方向平移至 .若四边形 的面积为 ,则阴影部分面积为. 16. 在平面直角坐标系 中,点 , , 在双曲线 上,且 , .则下列结论正确的有.(填写相应的序号即可)
16. 在平面直角坐标系 中,点 , , 在双曲线 上,且 , .则下列结论正确的有.(填写相应的序号即可)①若 且 ,则 为等腰三角形;
②若 且 ,则 为直角三角形;
③若 为等腰三角形,则 且 ;
④若 为直角三角形,则 且 .
三、解答题
-
17. 解不等式组: .18. 如图,四边形 是平行四边形,E,F是对角线 的三等分点.求证: .
 19. 先化简,再求值: ,其中20. 有两把不同的锁A,B和三把钥匙a,b,c,锁和钥匙的匹配情况如表所示.
19. 先化简,再求值: ,其中20. 有两把不同的锁A,B和三把钥匙a,b,c,锁和钥匙的匹配情况如表所示.锁
A
B
开锁钥匙
a
b c
(1)、随机抽出一把钥匙恰好可以打开B锁的概率是多少?(2)、随机取出一把钥匙开任意一把锁,一次开锁钥匙开锁的概率是多少?21. 如图,在 中, , 绕B点逆时针旋转45°后得到 ,其中点A的对应点是E,点C的对应点是F. (1)、求作 ;(要求:尺规作图,不写作法,保留痕迹)(2)、求证: .22. 某公司计划组织员工去武夷山风景区三日游,人数估计在 人.已知某旅行社的收费方案为:如果人数超过20人且不超过30人,人均收费为1000元;如果超过30人且不超过50人,则每增加1人,人均收费降低10元.设该公司旅游人数为x(人),人均收费为y(元).(1)、求y与x之间的关系式;.(2)、若旅行社此次带团的导游工资和车辆等固定成本为6000元,游客的吃住和门票等其他成本为600元/人.请你分析:旅行社带团接待旅游人数多少人时,旅行社所获利润w(元)最大,最大利润是多少?(利润=总收费-固定成本-其他成本)23. 如图是某校校史荣誉室的正方形网格平面图,实线表示墙体或门.在点 处安装了360度旋转摄像头,由于墙体的的遮挡,阴影部分无法监控,这部分无法监控到的区域通常称为监控盲区.
(1)、求作 ;(要求:尺规作图,不写作法,保留痕迹)(2)、求证: .22. 某公司计划组织员工去武夷山风景区三日游,人数估计在 人.已知某旅行社的收费方案为:如果人数超过20人且不超过30人,人均收费为1000元;如果超过30人且不超过50人,则每增加1人,人均收费降低10元.设该公司旅游人数为x(人),人均收费为y(元).(1)、求y与x之间的关系式;.(2)、若旅行社此次带团的导游工资和车辆等固定成本为6000元,游客的吃住和门票等其他成本为600元/人.请你分析:旅行社带团接待旅游人数多少人时,旅行社所获利润w(元)最大,最大利润是多少?(利润=总收费-固定成本-其他成本)23. 如图是某校校史荣誉室的正方形网格平面图,实线表示墙体或门.在点 处安装了360度旋转摄像头,由于墙体的的遮挡,阴影部分无法监控,这部分无法监控到的区域通常称为监控盲区. (1)、小红同学进入校史荣誉室随意参观,站在监控盲区的概率是多少?(2)、为了监控效果更好,使得监控盲区最小,请你帮助学校在墙体 上重新设计摄像头安装的位置,画出示意图,并说明理由.
(1)、小红同学进入校史荣誉室随意参观,站在监控盲区的概率是多少?(2)、为了监控效果更好,使得监控盲区最小,请你帮助学校在墙体 上重新设计摄像头安装的位置,画出示意图,并说明理由.
