福建省泉州市2021年数学中考二模试卷

试卷更新日期：2021-06-24 类型：中考模拟

进入出卷网下载

一、单选题

1. ﹣ $\frac{1}{5}$ 的绝对值是（）

A、﹣ $\frac{1}{5}$ B、 $\frac{1}{5}$ C、﹣5 D、5

查看试题解析
2. 截至2021年2月3日，“天问一号”火星探测器总飞行里程已超过4.5亿公里，距地球约170000000公里.将数字170000000用科学记数法表示为（）.

A、 $1.7 \times 10^{8}$ B、 $17 \times 10^{7}$ C、 $0.17 \times 10^{9}$ D、 $170 \times 10^{6}$

查看试题解析
3. 下列图形中既是轴对称图形又是中心对称图形的是（　　）

A、 B、 C、 D、

查看试题解析
4. 下列运算正确的是（）.

A、 $a^{2} \times a^{3} = a^{5}$ B、 $a^{2} + a^{3} = a^{5}$ C、 ${(a^{3})}^{2} = a^{5}$ D、 ${(3 a)}^{2} = 6 a^{2}$

查看试题解析
5. 如图，该几何体的左视图是（）

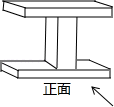A、 B、 C、 D、

查看试题解析
6. 下列事件中，是随机事件的是（）.

A、从背面朝上的5张红桃和5张梅花扑克牌中抽取一张牌，恰好是方块 B、抛掷一枚普通硬币9次是正面，抛掷第10次恰好是正面 C、从装有10个黑球的不透明箱子中随机摸出1个球，恰好是黑球 D、抛掷一枚质地均匀的正方体骰子，出现的点数不是奇数就是偶数

查看试题解析
7. 如图，数轴上两点M、N所对应的实数分别为m、n，则 $m + n$ 的结果可能是（）.

A、1 B、 $\frac{1}{2}$ C、0 D、－1

查看试题解析
8. 如图，在矩形 $A B C D$ 中，对角线 $A C$ 与 $B D$ 相交于点O， $E O ⊥ A C$ 于点O，交 $B C$ 于点E，若 $△ A B E$ 的周长为5， $A B = 2$ ，则 $A D$ 的长为（）.

A、2 B、2.5 C、3 D、4

查看试题解析
9. 如图，在 $6 \times 6$ 的网格图中， $⊙ O$ 经过格点A、B、D，点C在格点上，连接 $A C$ 交 $⊙ O$ 于点E，连接 $B D$ 、 $D E$ ，则 $\sin ∠ B D E$ 值为（）.

A、 $\frac{1}{2}$ B、 $\frac{\sqrt{5}}{5}$ C、 $\frac{2 \sqrt{5}}{5}$ D、2

查看试题解析
10. 已知二次函数 $y = a x^{2} - 2 a x + 3 (a > 0)$ ，当 $0 \leq x \leq m$ 时， $3 - a \leq y \leq 3$ ，则m的取值范围为（）.

A、 $0 \leq m \leq 1$ B、 $0 \leq m \leq 2$ C、 $1 \leq m \leq 2$ D、 $m \geq 2$

查看试题解析

二、填空题

11. 不等式2x﹣6＞0的解集是．

查看试题解析
12. 若n边形的每一个外角都为45°，则n的值为.

查看试题解析
13. 某校数学课外兴趣小组10个同学数学素养测试成绩如图所示，则该兴趣小组10个同学的数学素养测试成绩的众数是分.

查看试题解析
14. 若 $x - 2 y^{2} = - 4$ ，则 $- 3 x + 6 y^{2}$ 的值为..

查看试题解析
15. 如图所示的图案是我国汉代数学家赵爽在注解《周髀算经》中“赵爽弦图”经修饰后的图形，四边形 $A B C D$ 与四边形 $E F G H$ 均为正方形，点H是 $D E$ 的中点，阴影部分的面积为24，则 $A D$ 的长为..

查看试题解析
16. 如图，点A、C为反比例函数 $y_{1} = - \frac{6}{x}$ 上的动点，点B、D为反比例函数 $y_{2} = \frac{2}{x}$ 上的动点，若四边形 $A B C D$ 为菱形，则该菱形边长的最小值为.

查看试题解析

三、解答题

17. 解方程组： ${\begin{matrix} 4 x - 3 y = 11 \\ 2 x + y = 13 \end{matrix}$ .

查看试题解析
18. 先化简，再求值. $(\frac{a}{a + 1} - 1) \div \frac{a^{2} - 1}{a^{2} + 2 a + 1}$ ，其中 $a = 1 + \sqrt{2}$ .

查看试题解析
19. 如图，在▱ABCD中，点E、F分别在边CB、AD的延长线上，且BE＝DF，EF分别与AB、CD交于点G、H，求证：AG＝CH.

查看试题解析
20. 如图三角形纸片 $A B C$ 中， $∠ A = 30 °$ ， $A C = \sqrt{3}$ ，点P为 $A B$ 边上的一点（点P不与点A、B重合），连接 $C P$ ，将 $△ A C P$ 沿着 $C P$ 折叠得到 $△ A^{'} C P$ .

(1)、求作 $△ A^{'} C P$ ；（要求：尺规作图，不写作法，保留作图痕迹）

(2)、若 $∠ B P A^{'} = 30 °$ ，求点P到直线 $A C$ 的距离.

查看试题解析
21. 如图，在 $R t △ A B C$ 中， $∠ C = 90 °$ ， $A C = 8$ ， $B C = 6$ ，将 $△ A B C$ 绕点B按顺时针方向旋转得到 $△ D B E$ ，当点E恰好落在线段 $A B$ 上时，连接 $A D$ ， $∠ A B D$ 的平分线 $B F$ 交 $A D$ 于点F，连接 $E F$ .

(1)、求 $E F$ 的长；

(2)、求证：C、E、F三点共线.

查看试题解析

22. 某超市销售一款果冻，4月底以22元/千克购入200千克，5月10日再以22.5元/千克购入120千克.下表是这些果冻的销售记录，图象是其销售利润y（元）与销售量x（千克）之间的函数关系.

时间	销售记录
5月1日至7日	售价25元/千克，一共售出150千克
5月8日至9日	“五一”长假结束，这两天以成本价促销
5月10日至20日	售价25元/千克，全部售完，共获利780元

请根据上述信息，解答问题：

(1)、5月1日至7日，该超市销售这款果冻共获利多少元？

(2)、求5月10日至5月20日期间销售利润y（元）与销售量x（千克）之间的函数关系式，并直接写出x的取值范围.

查看试题解析

23. 随着互联网的快速发展，人们的生活越来越离不开快递，某快递公司邮寄每件包裹的收费标准是：重量小于或等于1千克的收费10元；重量超过1千克的部分，每超过1千克（不足1千克按1千克计算）需再收费2元.下表是该公司某天9：00～10：00统计的收件情况：

重量G（千克）	$0 < G \leq 1$	$1 < G \leq 2$	$2 < G \leq 3$	$3 < G \leq 4$	$4 < G \leq 5$	$G > 5$
件数	135	140	110	65	50	0

试根据以上所提供的信息，解决下列问题：

(1)、求包裹重量为1＜G≤2的概率；

(2)、小东打算在该公司邮寄一批每件3千克的包裹到不同地方，现有两种付费方式供他选择：①按该公司收费标准付费；②按上表中的平均费用付费.问：他选择哪种方式付费合算？说明理由.

查看试题解析

24. 如图1，在 $⊙ O$ 中，点A是优弧 $\overset{⌢}{B A C}$ 上的一点，点I为 $△ A B C$ 的内心，连接 $A I$ 并延长交 $⊙ O$ 于点D，连接 $O D$ 交 $B C$ 于点E，连接 $B I$ .

(1)、求证： $O D ⊥ B C$ ；

(2)、连接 $D B$ ，求证： $D B = D I$ ；

(3)、如图2，若 $B C = 24$ ， $\tan ∠ O B C = \frac{5}{12}$ ，当B、O、I三点共线时，过点D作 $D G // B I$ ，交 $⊙ O$ 于点G，求 $D G$ 的长.

查看试题解析
25. 已知顶点为D的抛物线 $y = a {(x - 3)}^{2} (a \neq 0)$ 交y轴于点 $C (0 ， 3)$ ，且与直线l交于不同的两点A、B（A、B不与点D重合）.

(1)、求抛物线的解析式；

(2)、若 $∠ A D B = 90 °$ ，
①试说明：直线l必过定点；

②过点D作 $D F ⊥ l$ ，垂足为点F，求点C到点F的最短距离.

查看试题解析