贵州省盘州市2021届高三理数上学期第一次模拟考试试卷
试卷更新日期:2021-06-24 类型:高考模拟
一、单选题
-
1. 已知集合 和 ,若 ,则 ( )A、0 B、-1 C、1 D、22. 在复平面内, 为原点,四边形 是复平面内的平行四边形,且 , , 三点对应的复数分别为 , , ,若 , ,则 ( )A、 B、 C、 D、3. 2020年1月17日,国家统计局发布了2019年全国居民人均消费支出及其构成的情况,并绘制了如图的饼图.根据饼图判断,下列说法不正确的是( )
 A、 2019年居民在“生活用品及服务”上人均消费支出的占比为6% B、2019年居民人均消费支出为21350元 C、2019年居民在“教育文化娱乐”上人均消费支出小于这8项人均消费支出的平均数 D、2019年居民在“教育文化娱乐”、“生活用品及服务”、“衣着”上的人均消费支出之和大于在“食品烟酒”上的人均消费支出4. 已知平面 , 满足 , ,过平面 和 外的一点 作直线 ,则“ ”是“ ”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件5. 已知定义在 上的奇函数 在 上单调递减若 ,则满足 的 的取值范围是( )A、 B、 C、 D、6. 已知数列 满足 , ,设 ,则数列 的前6项和为( )A、127 B、255 C、31 D、637. 已知双曲线 的右焦点为 ,若 到直线 的距离为 ,则 的离心率为( )A、2 B、 C、 D、8. 面直角坐标系 中,角 的顶点为 ,始边为 轴非负半轴,若点 是角 终边上的一点,则角 的值是( )A、 B、 , C、 , D、 ,9. 已知抛物线 的焦点为 ,设 和 是 上的两点,且 是线段 的中点,若 ,则 到 轴的距离的最小值是( )A、2 B、4 C、6 D、810. 已知两个非零向量 , 的夹角为120°,且满足 ,则 与 的夹角的大小为( )A、30° B、60° C、90° D、150°11. 已知函数 ,若函数 的图象与 的图象有3个交点,则 的取值范围是( )A、 B、 C、 D、12. 在数学中,若干有关联的曲线经过叠加或组合可以形成一些形状优美、寓意美好的曲线,如图的“心形”曲线 恰好就是曲线 和曲线 组合而成的,则曲线 所围成的“心形”区域的面积等于( )
A、 2019年居民在“生活用品及服务”上人均消费支出的占比为6% B、2019年居民人均消费支出为21350元 C、2019年居民在“教育文化娱乐”上人均消费支出小于这8项人均消费支出的平均数 D、2019年居民在“教育文化娱乐”、“生活用品及服务”、“衣着”上的人均消费支出之和大于在“食品烟酒”上的人均消费支出4. 已知平面 , 满足 , ,过平面 和 外的一点 作直线 ,则“ ”是“ ”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件5. 已知定义在 上的奇函数 在 上单调递减若 ,则满足 的 的取值范围是( )A、 B、 C、 D、6. 已知数列 满足 , ,设 ,则数列 的前6项和为( )A、127 B、255 C、31 D、637. 已知双曲线 的右焦点为 ,若 到直线 的距离为 ,则 的离心率为( )A、2 B、 C、 D、8. 面直角坐标系 中,角 的顶点为 ,始边为 轴非负半轴,若点 是角 终边上的一点,则角 的值是( )A、 B、 , C、 , D、 ,9. 已知抛物线 的焦点为 ,设 和 是 上的两点,且 是线段 的中点,若 ,则 到 轴的距离的最小值是( )A、2 B、4 C、6 D、810. 已知两个非零向量 , 的夹角为120°,且满足 ,则 与 的夹角的大小为( )A、30° B、60° C、90° D、150°11. 已知函数 ,若函数 的图象与 的图象有3个交点,则 的取值范围是( )A、 B、 C、 D、12. 在数学中,若干有关联的曲线经过叠加或组合可以形成一些形状优美、寓意美好的曲线,如图的“心形”曲线 恰好就是曲线 和曲线 组合而成的,则曲线 所围成的“心形”区域的面积等于( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 若实数 , 满足不等式组 则 的最大值是.14. 小明在一个专用的邮票箱中,收藏了北京2022年冬奥会吉祥物“冰墩墩”和冬残奥会吉样物“雪容融”纪念邮票一套2枚,北京2008年奥运会纪念邮票一套5枚.现从这7枚邮票中随机抽取3枚,恰好有“冰墩墩”图案和“雪容融”图案这2枚的概率为.
 15. “垛积术”在我国古代早期主要用于天文历法,后来用于求高阶等差级数的和.元代数学家朱世杰在沈括(北宋时期数学家)、杨辉(南宋时期数学家)研究成果的基础上,在《四元玉鉴》中利用了“三角垛”求一系列重要的高阶等差级数的和.例如,欲求数列 , , ,…, , 的和,可设计一个正立的 行三角数阵,即正三角形 的区域中所有数的分布规律为:第1行为1个 ,第2行为2个 ,第3行为3个 ,…,第 行为 个1;再选一个数列 (其前 项和已知),可设计一个倒立的 行三角数阵,即正三角形 的区域中所有数的分布规律为:第1行为 个 ,第2行为 个 ,第3行为 个 ,…,第 行为1个1.这两个三角数阵就组成一个 行 列的菱形数阵.若已知 ,则运用垛积术,求得数列 , , ,…, , 的和为.
15. “垛积术”在我国古代早期主要用于天文历法,后来用于求高阶等差级数的和.元代数学家朱世杰在沈括(北宋时期数学家)、杨辉(南宋时期数学家)研究成果的基础上,在《四元玉鉴》中利用了“三角垛”求一系列重要的高阶等差级数的和.例如,欲求数列 , , ,…, , 的和,可设计一个正立的 行三角数阵,即正三角形 的区域中所有数的分布规律为:第1行为1个 ,第2行为2个 ,第3行为3个 ,…,第 行为 个1;再选一个数列 (其前 项和已知),可设计一个倒立的 行三角数阵,即正三角形 的区域中所有数的分布规律为:第1行为 个 ,第2行为 个 ,第3行为 个 ,…,第 行为1个1.这两个三角数阵就组成一个 行 列的菱形数阵.若已知 ,则运用垛积术,求得数列 , , ,…, , 的和为.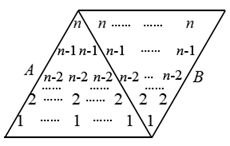 16. 在四棱锥 中,侧面 底面 ,底面 为矩形, , , ,则异面直线 与 所成角的大小为;四棱锥 外接球的表面积为.
16. 在四棱锥 中,侧面 底面 ,底面 为矩形, , , ,则异面直线 与 所成角的大小为;四棱锥 外接球的表面积为.三、解答题
-
17. 在 中,内角 、 、 的对边分别为 、 、 ,且 .
 (1)、求 ;(2)、已知 , ,延长 至 ,使得 ,求 .18. 如图,圆锥的顶点为 , 是底面圆 的直径, 是圆 上异于 、 的一点, 是 的中点,平面 平面 , .
(1)、求 ;(2)、已知 , ,延长 至 ,使得 ,求 .18. 如图,圆锥的顶点为 , 是底面圆 的直径, 是圆 上异于 、 的一点, 是 的中点,平面 平面 , . (1)、求证: ;(2)、若 与 所成的角为60°,求 与平面 所成角的正弦值.19. 某花店为了拓展业务范围,根据一些公司在店庆,开业等活动中的需要,推行了“发财树”和“元宝树”的出租业务.为了调查“发财树”和“元宝树”这两种树的出租情况,现随机抽取了这两种树各20盆,分别统计了每种树在4天中的出租天数和出租盆数(假设出租“发财树”与“元宝树”互不影响),并绘制成如下的条形图:
(1)、求证: ;(2)、若 与 所成的角为60°,求 与平面 所成角的正弦值.19. 某花店为了拓展业务范围,根据一些公司在店庆,开业等活动中的需要,推行了“发财树”和“元宝树”的出租业务.为了调查“发财树”和“元宝树”这两种树的出租情况,现随机抽取了这两种树各20盆,分别统计了每种树在4天中的出租天数和出租盆数(假设出租“发财树”与“元宝树”互不影响),并绘制成如下的条形图:
以这4天中的频率作为概率,解答以下问题:
(1)、估计该花店一盆“发财树”和一盆“元宝树”在这4天中合计出租天数恰好为3天的概率;(2)、如果一盆“发财树”和一盆“元宝树”每天出租所获得的利润都为40元,那么,对于该花店“发财树和“元宝树”,哪一种出租平均获利较多?并说明你的理由.20. 已知椭圆 的离心率为 ,短轴的下端点 的坐标为 .(1)、求椭圆 的方程;(2)、设 , 是椭圆 上异于 且不关于 轴对称的两点, , 的中点为 ,求证:点 在定直线上运动.21. 已知函数 .(1)、当 时,求 的极值;(2)、是否存在实数 ,使得当 时, 恒成立?若存在,求出 的取值范围;若不存在,请说明理由.22. 第三届中国国际进口博览会的建筑主体为“四叶草”造型,“四叶草”是绿色的有生命力的象征,其优美的曲线与江南地区海派文化的优雅唯美气质相应和,表达了中国对未来经济持续发展、人民生活富裕的美好向往;“四叶草”作为世界通用的吉祥图形,四瓣叶子分别寓意着“至爱、健康、荣誉、富裕”,整体带有吉祥、和谐的意义如图,在极坐标系 中,方程 表示的图形为“四叶草”对应的曲线 . (1)、设直线 与 交于异于 的两点 , ,求 、 两点的极坐标;(2)、设 、 是 上异于 的两点,求 的最大值.23. 已知函数 .(1)、求不等式 的解集;(2)、若存在 ,使得 成立,求实数 的取值范围.
(1)、设直线 与 交于异于 的两点 , ,求 、 两点的极坐标;(2)、设 、 是 上异于 的两点,求 的最大值.23. 已知函数 .(1)、求不等式 的解集;(2)、若存在 ,使得 成立,求实数 的取值范围.