初中数学苏科版九年级上册 第二章 对称图形——圆 综合测试卷
试卷更新日期：2021-06-24 类型：单元试卷
一、单选题
-
1. 如图，王老师将汽车停放放置在地面台阶直角处，他测量了台阶高 为 ，汽车轮胎的直径为 ，请你计算直角顶点到轮胎与底面接触点 长为（ ）.
A、 B、 C、 D、2. 如图，在半径2的圆形纸片中，剪一个圆心角为90°的扇形（图中阴影部分），则这个扇形的面积为（ ）
A、π B、 C、2π D、3. 如图，点A，B，C，D在 上， ，若 ，则 的度数为（ ）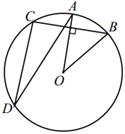
A、20° B、25° C、30° D、40°4. 如图，在等腰Rt△ABC中，∠C＝90°，AC=BC=4，以A为圆心、AC长为半径作弧，交AB于点D，则阴影部分的面积是（ ）
A、 B、 C、 D、5. 如图，AB是半圆的直径，O是圆心，C是半圆上的点，D是 上的点，若∠BOC ＝ 50°，则∠D的大小为（ ）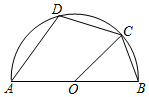
A、100° B、105° C、110° D、115°6.如图，⊙O的半径为2，点O到直线l的距离为3，点P是直线l上的一个动点，PQ切⊙O于点Q，则PQ的最小值为（ ）
A、 B、 C、3 D、5二、填空题
-
7. 小明用彩纸给爸爸做一顶生日帽，其左视图和俯视图如图所示，其中AB=24 cm，AC=36 cm，则至少需用彩纸cm2（接口处重叠面积不计）.
8. 如图，已知⊙O的半径为m，点C在直径AB延长线上，BC=m.在过点C的任一直线l上总存在点P，使过P的⊙O的两切线互相垂直，则∠ACP的最大值等于.
9. 如图，在矩形 中， ， ， ， 分别是 ， 边上的点，若 经过点 ，且与 ， 分别相切于点 ， ，则 的半径为.
10. 用半径为6，圆心角为120°的扇形纸片围成一个圆锥的侧面，则这个圆锥的底面圆半径为.11. 已知圆锥的底面圆的半径是2.5，母线长是6，其侧面展开图的面积.12. 一个圆锥的主视图为边长等于 的等边三角形，则这个圆锥的侧面积为 .
13. 如图，小正方形的边长均为1，扇形OAB是某圆锥的侧面展开图，则这个圆锥的底面周长为.（结果保留π）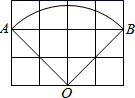
14. 圆锥的母线长为 ，侧面积为 ，则圆锥的底面圆半径 .15. 已知一圆锥的母线为 ，底面圆的直径为 ，则此圆锥的侧面积为 （保留 ）.16. 如图，在矩形ABCD中，AB＝4，AD＝6，点E是AD所在直线上的一点，过点A作AN⊥BE于N，点M是BC上一动点，连接NM，MD，则MN+MD的最小值为.
三、解答题
-
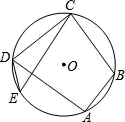
17. 四边形 ABCD 内接于⊙O，CB=CD，∠A=100°，点 E在 上，求∠E 的度数.
18. 如图1是某奢侈品牌的香水瓶，从正面看上去（如图2），它可以近似看作⊙O割去两个弓形（由弦及其所对的弧组成的图形叫做弓形）后余下的部分与矩形ABCD组合而成的图形（点B、C在⊙O上），其中BC∥EF；从侧面看，它是扁平的，厚度为1.3cm.已知⊙O的半径为2.5cm，BC=1.4cm，AB=3.1cm，EF=3cm，求香水瓶的高度h.
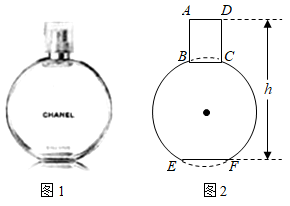19. 如图，在Rt△ABC中，∠ACB=90°，AC=3，BC=4，以点C为圆心，CA为半径的圆与AB交于点D.求AD的长.
20. 如图， ，D、E分别是半径OA和OB的中点，试判断CD与CE的大小关系，并说明理由.
21. ⊙O的半径为10cm，AB，CD是⊙O的两条弦，AB∥CD，AB=12cm，CD=16cm，求AB和CD之间的距离.22. 如图，在⊙O中，弦AB与弦CD相交于点M，且AB＝CD，求证：BM＝DM.
23. 如图所示，△ABC内接于⊙O，AB＝AC，D在 上，连接CD交AB于点E，B是 的中点，求证：∠B＝∠BEC.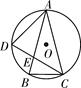
24. 已知：如图，AB为⊙O的直径，OD∥AC.求证：点D平分 .
25. 如图： ，D、E分别是半径OA和OB的中点，求证：CD＝CE.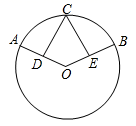
26. 如图，四边形 内接于 ， 与 为对角线， ，过点A作 交 的延长线于点E.求证： .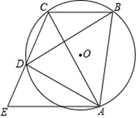
四、综合题
-
27.
如图，已知直线PA交⊙O于A、B两点，AE是⊙O的直径，点C为⊙O上一点，且AC平分∠PAE，过C作CD⊥PA，垂足为D．
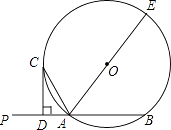(1)、求证：CD为⊙O的切线；(2)、若CD=2AD，⊙O的直径为20，求线段AC、AB的长．28. 如图，在 中， ，以O为圆心，以 的长为半径作 ，交 于点D，交 于点E，过点B和点O分别作 、 的平行线，交于点C，连结 .
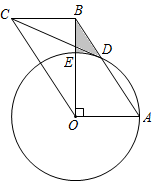(1)、若 ， ，求阴影部分的面积；(2)、试判断 与 的位置关系，并说明理由.29. 如图，⊙O是△ABC的外接圆，∠ABC＝45°，OC∥AD，AD交BC的延长线于D，AB交OC于E.
(1)、求证：AD是⊙O的切线；(2)、若AE＝2 ，CE＝4.求图中阴影部分（弦AC和劣弧AC围成的部分）的面积.30. 如图，四边形ABCD内接于⊙O，AC是⊙O的直径，过点B作BE⊥AD，垂足为点E，AB平分∠CAE.
(1)、判断BE与⊙O的位置关系，并说明理由；(2)、若∠ACB=30°，⊙O的半径为4，请求出图中阴影部分的面积.31. 在△ABC中，AB=AC=10，BC=12.△ABC的内切圆☉O与BC，AC，AB分别相切于点D，E，F，求：
(1)、AF，BD，CE的长；(2)、△ABC的内切圆的半径.32. 如图，点O在∠APB的平分线上，⊙O与PA相切于点C．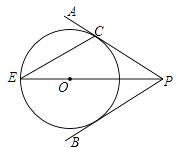
(1)、求证：直线PB与⊙O相切；
(2)、PO的延长线与⊙O交于点E．若⊙O的半径为3，PC=4．求弦CE的长．33. 如图，矩形OABC中，点A，点C分别在x轴，y轴上，D为边BC上的一动点，现把 沿OD对折，C点落在点P处，已知点B的坐标为 .
(1)、当D点坐标为 时，求P点的坐标；(2)、在点D沿BC从点C运动至点B的过程中，设点P经过的路径长度为 ，求 的值；(3)、在点D沿BC从点C运动至点B的过程中，若点P落在同一条直线 上的次数为2次，请直接写出k的取值范围.34. 如图，AB是⊙O的一条弦，点C是⊙O外一点， OC⊥OA，OC交AB于点P、交⊙O于点Q，且CP＝CB＝2.
(1)、求证：BC是⊙O的切线；(2)、若∠A＝22.5°，求图中阴影部分的面积.35. 如图，AC是⊙O的直径，点D是⊙O上一点，DE⊥AB，垂足为E，且∠EAD=∠CAD.
(1)、求证：BD=CD；(2)、求证：DE是⊙O的切线；(3)、若⊙O半径为5，BE=8，求AD的长.36. 问题探究
(1)、如图1，点A，B在直线l的同侧，请你在直线l上找一点P，使得AP+BP的值最小(不需要说明理由)；(2)、尝试体验：如图2，菱形ABCD的边长为6，对角线AC=6 ，点E，F在AC上，且EF=2，求DE+BF的最小值。
(3)、解决应用如图3，在四边形ABCD中，AB=AD=6，∠BAD=60°，∠BCD=120°，四边形ABCD的周长是否存在最大值？若存在，请求出最大值；若不存在，请说明理由。
37. 如图， 的平分线交 的外接圆于点 ， 的平分线交 于点 ．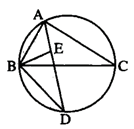
(1)、求证： ；(2)、若 ， ，求 外接圆的半径．38. 如图，在平面直角坐标系中，点A与点B关于原点O对称，点A ，点C ，点P在直线BC上运动.
(1)、连接AC、BC ，求证：△ABC是等边三角形；(2)、求点P的坐标，使∠APO= ；(3)、在平面内，平移直线BC，试探索：当BC在不 同位置时，使∠APO= 的点P的个数是否保持不变?若不变，指出点P的个数有几个?若改变，指出点P的个数情况，并简要说明理由.39. 如图，在⊙O的内接四边形ABCD中，AB＝AD，∠C＝120°，点E在上．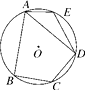
(1)、求∠AED的度数；
(2)、若⊙O的半径为2，则弧AD的长为多少？
(3)、连接OD，OE，当∠DOE＝90°时，AE恰好是⊙O内接正n边形的一边，求n的值．