初中数学苏科版八年级上册5.2 平面直角坐标系 同步练习
试卷更新日期：2021-06-22 类型：同步测试
一、单选题
-
1. 已知点 在第四象限，且点 到 轴， 轴的距离分别为 ．则点 的坐标为（ ）A、 B、 C、 D、2. 在平面直角坐标系中，点A的坐标为（-4，3），AB∥y轴，AB=5，则点B的坐标为（ ）A、（1，3） B、（-4，8） C、（-4，8）或（-4，-2） D、（1，3）或（-9，3）3. 已知点 在第二象限，且到 轴的距离为2，到 轴的距离为4，则 点坐标为（ ）A、（-4，2） B、（4，-2） C、（-2，4） D、（2，-4）4. 点 在y轴上，则点M的坐标为（ ）A、 B、 C、 D、5. 如图，在正方形网格中，若点 ，点 ，则点 的坐标为（ ）
A、 B、 C、 D、6. 课间操时，小明、小丽、小亮的位置如图所示，小明对小亮说：如果我的位置用（0，0）表示，小丽的位置用（2，1）表示，那么你的位置可以表示成（ ）
A、（5，4） B、（4，5） C、（3，4） D、（4，3）7. 若点M在第四象限，且M到x轴的距离为1，到y轴的距离为2，则点M的坐标为（ ）A、（1，﹣2） B、（2，1） C、（﹣2，l） D、（2，﹣l）8. 已知:点P( )在y轴上，则P点的坐标为（ ）A、（0，- ） B、（ ，0） C、（0， ） D、（- ，0）9. 根据下列表述，能确定具体位置的是（ ）A、我校八年级（1）班班级座位3排4列 B、滨海县育才路 C、东经118° D、县一中北偏东60°10. 已知点A在第四象限，且它到x轴的距离等于2，到y轴的距离等于3，则点A的坐标为（ ）A、（3，﹣2） B、（3，2） C、（2，﹣3） D、（2，3）二、填空题
-
11. 在平面直角坐标系中，第二象限内有一点M，点M到x轴的距离为5，到y轴的距离为4，则点M的坐标是.12. 在平面直角坐标系中，将点M（3，-1）沿x轴向左平移2个单位，再沿y轴向下平移3个单位后得到点N，则点N的坐标为.13. 在平面直角坐标系中，点A(2， )一定在第象限.14. 若点 在第三象限，则点 一定在第象限.15. 已知点 P（m-2，2m-1）在第二象限，且 m 为整数，则 m 的值是.16. 在平面直角坐标系中，O为坐标原点，点A坐标为（8，0），第一象限的动点P（m，n），且m＋n＝10．则当S△OPA＝12时，P点的坐标为 ．17. 在平面直角坐标系中，点A（2，1）向左平移3个单位长度，再向下平移4个单位后的坐标为.18. 在平面直角坐标系中，若点M（2，4）与点N（x，4）之间的距离是3，则x的值是.19. 已知点M（3，2）与点N（x，y）在同一条平行于x轴的直线上，且点N到y轴的距离为8，则点N的坐标为.20. 如图，在平面直角坐标系中，以点O为心，适当的长为半径画弧，交x轴于点M，交y轴于点N，再分别以从点M、N为圆心，大于 MN的长为半径画弧，两弧在第二象限交于点P，若点P的坐标（2a，a+1），则a＝.
三、解答题
-
21. 在平面直角坐标系中，已知A（0，0）、B（4，0），点C在y轴上，且△ABC的面积是12．求点C的坐标．
22.在我国沿海地区，几乎每年夏秋两季都会或多或少地遭受台风的侵袭，加强台风的监测和预报，是减轻台风灾害的重要措施．下表是中央气象台2010年发布的第13号台风“鲇鱼”的有关信息：
请在下面的经纬度地图上找到台风中心在16日23时和17日23时所在的位置．
23.如图的方格中有25个汉字，如四1表示“天”，请沿着以下路径去寻找你的礼物：
（1）一1→三2→二4→四3→五1
（2）五3→二1→二3→一5→三4
（3）四5→四1→一2→三3→五2．
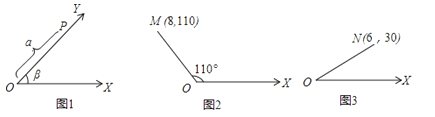
24.如图1，将射线OX按逆时针方向旋转β角，得到射线OY，如果点P为射线OY上的一点，且OP=a，那么我们规定用（a，β）表示点P在平面内的位置，并记为P（a，β），例如，图2中，如果OM=8，∠XOM=110°，那么点M在平面内的位置，记为M（8，110），根据图形，解答下面的问题：
（1）如图3，如果点N在平面内的位置记为N（6，30），那么ON各∠XON等于多少？
（2）如果点A、B在平面内的位置分别记为A（5，30），B（12，120），试求A、B两点之间的距离并画出图．
25.多多和爸爸、妈妈周末到公园游玩，回到家后，他利用平面直角坐标系画出了公园的景区地图，如图所示．可是他忘记了在图中标出原点和x轴、y轴．只知道牡丹园的坐标为（3，3），请你帮他建立平面直角坐标系（画在图中）并求出其它各景点的坐标？
26.如图，是某校的平面示意图，已知图书馆、行政楼的坐标分别为（﹣3，2），（2，3）．完成以下问题：
（1）请根据题意在图上建立直角坐标系；
（2）写出图上其他地点的坐标
（3）在图中用点P表示体育馆（﹣1，﹣3）的位置．
27.如图，A、B两点的坐标分别是（2，﹣3）、（﹣4，﹣3）．
（1）请你确定P（4，3）的位置；
（2）请你写出点Q的坐标．
28.如图，某小区有大米产品加工点3个（M1 ， M2 ， M3），大豆产品加工点4个（D1 ， D2 ， D3 ， D4），为了加强食品安全监督，政府要求对食品加工点进行网格化管理，管理员绘制了坐标网格和建立了平面直角坐标系（隐藏），把图中的大米加工点用坐标表示为M1（﹣5，﹣1），M2（4，4），M3（5，﹣4）．
（1）请你画出管理员所建立的平面直角坐标系；
（2）类似地，在所画平面直角坐标系内，用坐标表示出大豆产品加工点的位置．
29. 在平面直角坐标系中，点A的坐标是（3a﹣5，a+1）（1）若点A在y轴上，求a的值及点A的坐标．
（2）若点A到x轴的距离与到y轴的距离相等 ,求a的值及点A的坐标．
30. 如果B（m+1，3m﹣5）到x轴的距离与它到y轴的距离相等，求m．四、作图题
-
31.
（1）将图中三角形各点的横坐标都乘以-1，纵坐标不变，画出所得到的图形．你所画的图形与原图形发生了什么变化？
（2）若把原图中各点横坐标保持不变，纵坐标都乘以-2，画出所得到的图形，并说明该图与原图相比发生了什么变化？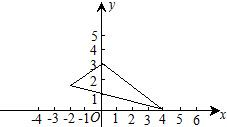
32. 小明家在学校以东150m，再往北100m处，张明同学家在学校以西50m，再往南200m处，王玲同学家在学校以南150m处，建立适当的直角坐标系，在直角坐标系中画出这三位同学家的位置，并用坐标表示出来．五、综合题
-
33. 在平面直角坐标系中，有 A（-2，a +1）， B（a -1，4）， C（b - 2，b）三点.(1)、当 AB// x轴时，求 A、 B两点间的距离；(2)、当CD⊥x轴于点 D，且CD = 1时，求点C的坐标.34. 在平面直角坐标系中，有点A（a+1，2），B（-a-5，2a+1）.(1)、若线段AB∥y轴，求点A、B的坐标；(2)、当点B到y轴的距离是到x轴的距离4倍时，求点B所在的象限位置.35. 在平面直角坐标系xOy中，有一点P（a，b），实数a，b，m满足以下两个等式：2a-6m+4=0，b+2m-8=0.(1)、当a=1时，点P到x轴的距离为；(2)、若点P在第一三象限的角平分线上，求点P的坐标；(3)、当a＜b时，则m的取值范围是.36. 已知点P（a﹣2，2a+8），分别根据下列条件求出点P的坐标.(1)、点P在x轴上；(2)、点P在y轴上；(3)、点Q的坐标为（1，5），直线PQ∥y轴；(4)、点P到x轴、y轴的距离相等.
