人教版初中数学八年级下学期期末考试模拟试卷
试卷更新日期:2021-06-22 类型:期末考试
一、单选题
-
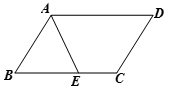
1. 下列运算正确的是( )A、 =﹣4 B、 ﹣ C、( )2=4 D、2. 如图所示,在平行四边形ABCD中,已知AD=5cm,AB=3cm,AE平分∠BAD交BC边于点E,则EC等于( )
 A、2 cm B、3 cm C、4 cm D、5 cm3. 已知二条线段的长分别为 ,那么能与它们组成直角三角形的第三条线段的长是( )A、 B、 C、 D、 与4. 古希腊几何学家海伦和我国宋代数学家秦九韶都曾提出利用三角形的三边求面积的公式,称为海伦﹣秦九韶公式:如果一个三角形的三边长分别是a,b,c,记 ,那么三角形的面积为 如图,在 中, , , 所对的边分别记为 , , ,若 , , ,则 的面积为( )
A、2 cm B、3 cm C、4 cm D、5 cm3. 已知二条线段的长分别为 ,那么能与它们组成直角三角形的第三条线段的长是( )A、 B、 C、 D、 与4. 古希腊几何学家海伦和我国宋代数学家秦九韶都曾提出利用三角形的三边求面积的公式,称为海伦﹣秦九韶公式:如果一个三角形的三边长分别是a,b,c,记 ,那么三角形的面积为 如图,在 中, , , 所对的边分别记为 , , ,若 , , ,则 的面积为( ) A、 B、 C、 D、5. 如图,长方体的长为8,宽为10,高为6,点B离点C的距离为2,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是( )
A、 B、 C、 D、5. 如图,长方体的长为8,宽为10,高为6,点B离点C的距离为2,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是( ) A、 B、 C、 D、6. 小明在计算一组数据的方差时,列出的公式如下 ,根据公式信息,下列说法中,错误的是( )A、数据个数是5 B、数据平均数是8 C、数据众数是8 D、数据方差是7. 直线y=kx+b和y=bx+k在同一平面直角坐标系中的大致图象可能是( )A、
A、 B、 C、 D、6. 小明在计算一组数据的方差时,列出的公式如下 ,根据公式信息,下列说法中,错误的是( )A、数据个数是5 B、数据平均数是8 C、数据众数是8 D、数据方差是7. 直线y=kx+b和y=bx+k在同一平面直角坐标系中的大致图象可能是( )A、 B、
B、 C、
C、 D、
D、 8. 一辆客车从甲地开往乙地,一辆出租车从乙地开往甲地,两车同时出发,两车距甲地的距离y(千米)与行驶时间x(时)之间的函数图象如图所示,则下列说法:①客车比出租车晚4小时到达目的地;②两车出发后3.75小时相遇;③两车相遇时客车距乙地还有225千米;④客车的速度为60千米/时,出租车的速度为100千米/时,其中正确的有( )
8. 一辆客车从甲地开往乙地,一辆出租车从乙地开往甲地,两车同时出发,两车距甲地的距离y(千米)与行驶时间x(时)之间的函数图象如图所示,则下列说法:①客车比出租车晚4小时到达目的地;②两车出发后3.75小时相遇;③两车相遇时客车距乙地还有225千米;④客车的速度为60千米/时,出租车的速度为100千米/时,其中正确的有( ) A、1个 B、2个 C、3个 D、4个9. 已知:将直线 向左平移2个单位长度后得到直线 ,则下列关于直线 的说法正确的是( )A、经过第一、二、三象限 B、与x轴交于 C、与y轴交于 D、y随x的增大而减小10. 如图,平行四边形 的周长为40, 的周长比 的周长多10,则 为( )
A、1个 B、2个 C、3个 D、4个9. 已知:将直线 向左平移2个单位长度后得到直线 ,则下列关于直线 的说法正确的是( )A、经过第一、二、三象限 B、与x轴交于 C、与y轴交于 D、y随x的增大而减小10. 如图,平行四边形 的周长为40, 的周长比 的周长多10,则 为( ) A、5 B、20 C、10 D、1511. 如图,在 中, , , ,若两阴影部分都是正方形, 、 、 在一条直线上,且它们的面积之比为 ,则较大的正方形的面积是( )
A、5 B、20 C、10 D、1511. 如图,在 中, , , ,若两阴影部分都是正方形, 、 、 在一条直线上,且它们的面积之比为 ,则较大的正方形的面积是( ) A、36 B、27 C、18 D、912. 如图,菱形ABCD的周长为40 cm,对角线AC,BD相交于点O,DE⊥AB,垂足为E,DE∶AB=4∶5,下列结论:①DE=8 cm;②BE=4 cm;③BD=4 cm;④AC=8 cm;⑤S菱形ABCD=80 cm2.其中正确的有( )
A、36 B、27 C、18 D、912. 如图,菱形ABCD的周长为40 cm,对角线AC,BD相交于点O,DE⊥AB,垂足为E,DE∶AB=4∶5,下列结论:①DE=8 cm;②BE=4 cm;③BD=4 cm;④AC=8 cm;⑤S菱形ABCD=80 cm2.其中正确的有( ) A、①②④⑤ B、①②③④ C、①③④⑤ D、①②③④⑤
A、①②④⑤ B、①②③④ C、①③④⑤ D、①②③④⑤二、填空题
-
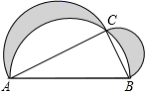
13. 若函数 是一次函数,则m的值为 .14. 若x<2,化简 的正确结果是.15. 已知 ﹣ =2,则 的值为 .16. 如图: , 的面积为20,在 的同侧,分别以 , , 为直径作三个半圆,则阴影部分(即“希波克拉底月牙形”)的面积为.
 17. 如图,平行四边形 中, 于点E,点F为边AB的中点,连接EF,CF,若 , ,则 .
17. 如图,平行四边形 中, 于点E,点F为边AB的中点,连接EF,CF,若 , ,则 . 18. 如图, ABCD的顶点B在矩形AEFC的边EF上,点B与点E、F不重合.若△ACD的面积为3,则图中的阴影部分两个三角形的面积和为
18. 如图, ABCD的顶点B在矩形AEFC的边EF上,点B与点E、F不重合.若△ACD的面积为3,则图中的阴影部分两个三角形的面积和为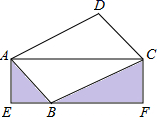 19. 小明参加了步行活动中,中途休息了一段时间.设他从学校出发后所用时间为 (分钟),所走的路程为 (米 ,s与t之间的函数关系如图17所示.则下列说法中,正确的序号为 .
19. 小明参加了步行活动中,中途休息了一段时间.设他从学校出发后所用时间为 (分钟),所走的路程为 (米 ,s与t之间的函数关系如图17所示.则下列说法中,正确的序号为 .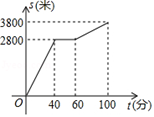
①小明中途休息用了20分钟.
②小明休息前步行的平均速度为每分钟70米.
③小明休息前步行的平均速度大于休息后步行的平均速度.
④小明行走的路程为6600米.
20. 如图,在▱ABCD中,CH⊥AD于点H, CH与BD的交点为E.如果∠1=70°,∠ABC=3∠2,那么∠ADC=
三、计算题
-
21. 化简:(1)、(2)、
四、综合题
-
22. 第31届世界大学生夏季运动会计划于2021年8月在成都举行,武侯区某学校开展“爱成都,迎大运”活动的小主持人选拔赛,对A,B,C,D四名候选人进行了笔试和面试(各项成绩满分均为100分),他们的各项成绩如表所示:
学生
笔试成绩/分
面试成绩/分
A
90
86
B
84
90
C
x
88
D
86
84
(1)、填空:这四名候选人的面试成绩的中位数是分;(2)、学校按笔试成绩占60%、面试成绩占40%的方式确定候选人的综合成绩(满分为100分),若候选人C的综合成绩为86.2分,求表中x的值;(3)、在(2)的条件下,分别求其余三名候选人的综合成绩,如果学校将根据综合成绩遴选两名小主持人,试问哪两名候选人将被录取?23. 如图,在△ABC中,AB=AC,BC=15,D是AB上一点,BD=9,CD=12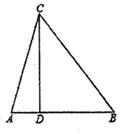 (1)、求证:CD⊥AB;(2)、求AC长24. 如图,在平行四边形ABCD中,对角线AC , BD交于点O , 过点O作直线EF⊥AB , 分别交AB , CD于点E , F .
(1)、求证:CD⊥AB;(2)、求AC长24. 如图,在平行四边形ABCD中,对角线AC , BD交于点O , 过点O作直线EF⊥AB , 分别交AB , CD于点E , F .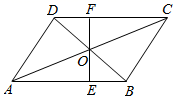 (1)、求证:OE=OF;(2)、若AC=18,EF=10,求AE的长.25. 如图1所示,在A,B两地之间有汽车站C站,客车由A地驶往B地,货车由B地驶往C站.两车同时出发,匀速行驶.图2是客车、货车离C站的路程y1、y2(千米)与行驶时间x(小时)之间的函数关系图象.
(1)、求证:OE=OF;(2)、若AC=18,EF=10,求AE的长.25. 如图1所示,在A,B两地之间有汽车站C站,客车由A地驶往B地,货车由B地驶往C站.两车同时出发,匀速行驶.图2是客车、货车离C站的路程y1、y2(千米)与行驶时间x(小时)之间的函数关系图象.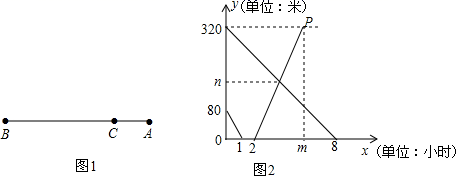 (1)、填空:A,B两地相距千米,图2中的m的值为;(2)、求两小时后,客车离C站的路程y2与行驶时间x之间的函数关系式;(3)、指出图2中n的实际意义,并求出n的值.26. 如图,在平行四边形 中, 的平分线交 于点E,交 的延长线于F,以 为邻边作平行四边形 。
(1)、填空:A,B两地相距千米,图2中的m的值为;(2)、求两小时后,客车离C站的路程y2与行驶时间x之间的函数关系式;(3)、指出图2中n的实际意义,并求出n的值.26. 如图,在平行四边形 中, 的平分线交 于点E,交 的延长线于F,以 为邻边作平行四边形 。 (1)、证明平行四边形 是菱形;(2)、若 ,连结 ,①求证: ;②求 的度数;(3)、若 , , ,M是 的中点,求 的长。
(1)、证明平行四边形 是菱形;(2)、若 ,连结 ,①求证: ;②求 的度数;(3)、若 , , ,M是 的中点,求 的长。
-