辽宁省沈阳市皇姑区2021年中考数学二模试卷
试卷更新日期:2021-06-22 类型:中考模拟
一、单选题
-
1. 如果水位升高3m时水位变化记作+3m,那么水位下降3m时水位变化记作( )A、-3m B、3 m C、6 m D、-6 m2. 仔细观察图所示的两个物体,则它的俯视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、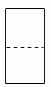 3. 我国自主研发的“北斗系统”现已广泛应用于国防、生产和生活等各个领域,多项技术处于国际领先地位,其星载原子钟的精度,已经提升到了每3000000年误差1秒.数3000000用科学记数法表示为( )A、 B、 C、 D、4. 下列计算正确的是( )A、 B、 C、 D、5. 下列命题的逆命题是真命题的是( )A、若 ,则 B、同位角相等,两直线平行 C、对顶角相等 D、若 , ,则6. 实数a , b在数轴上对应点的位置如图所示,则下列结论正确的是( )
3. 我国自主研发的“北斗系统”现已广泛应用于国防、生产和生活等各个领域,多项技术处于国际领先地位,其星载原子钟的精度,已经提升到了每3000000年误差1秒.数3000000用科学记数法表示为( )A、 B、 C、 D、4. 下列计算正确的是( )A、 B、 C、 D、5. 下列命题的逆命题是真命题的是( )A、若 ,则 B、同位角相等,两直线平行 C、对顶角相等 D、若 , ,则6. 实数a , b在数轴上对应点的位置如图所示,则下列结论正确的是( ) A、 B、 C、 D、7. 已知三角形两边长分别为3和8,则该三角形第三边的长可能是( )A、5 B、10 C、11 D、128. 已知圆的半径是2 ,则该圆的内接正六边形的面积是( )
A、 B、 C、 D、7. 已知三角形两边长分别为3和8,则该三角形第三边的长可能是( )A、5 B、10 C、11 D、128. 已知圆的半径是2 ,则该圆的内接正六边形的面积是( )
A、3 B、9 C、18 D、369. 为迎接“六一”儿童节,某儿童品牌玩具专卖店购进了甲、乙两类玩具,其中甲类玩具的进价比乙类玩具的进价每个多5元,经调查:用1000元购进甲类玩具的数量与用750元购进乙类玩具的数量相同.设甲类玩具的进价为x元/个,根据题意可列方程为( )A、 B、 C、 D、10. 抛物线 图象如图所示,则下面一次函数 与反比例函数 在同一平面直角坐标系内的图象大致为( ) A、
A、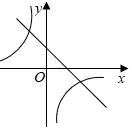 B、
B、 C、
C、 D、
D、
二、填空题
-
11. 分解因式: .12. 抛物线 向右平移1个单位,再向下平移2个单位,平移后的抛物线的顶点坐标是 .13. 已知杭州市某天六个整点时的气温绘制成的统计图,则这六个整点时气温的中位数是.
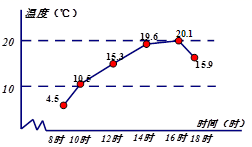 14. 给出一种运算: ,那么 .15. 如图,已知 ,则 的度数是.
14. 给出一种运算: ,那么 .15. 如图,已知 ,则 的度数是.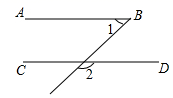 16. 如图,在边长为 的正方形 中,点 分别是边 的中点,连接 点 分别是 的中点,连接 ,则 的长度为.
16. 如图,在边长为 的正方形 中,点 分别是边 的中点,连接 点 分别是 的中点,连接 ,则 的长度为.
三、解答题
-
17. 先化简,再求值: ,其中 .18. 小华有三张卡片,小明有两张卡片,卡片除正面上的数字不同外其它都相同,卡片上的数字如图所示.小华从自己的三张卡片中随机抽取一张,之后小明也从自己的两张卡片中随机抽取一张,请用画树状图(或列表)的方法,求抽取的两张卡片上的数字和为7的概率.
 19. 为了解“停课不停学”过程中学生对网课内容的喜爱程度,某校开展了一次网上问卷调查.随机抽取部分学生,按四个类别统计,其中A表示“很喜欢”,B表示“喜欢”,C表示“一般”,D表示“不喜欢”,并将调查结果绘制成下面两幅不完整的统计图.
19. 为了解“停课不停学”过程中学生对网课内容的喜爱程度,某校开展了一次网上问卷调查.随机抽取部分学生,按四个类别统计,其中A表示“很喜欢”,B表示“喜欢”,C表示“一般”,D表示“不喜欢”,并将调查结果绘制成下面两幅不完整的统计图.
请根据图中提供的信息,解决下列问题:
(1)、这次共抽取名学生进行统计调查,扇形统计图中D类所在扇形的圆心角度数为;(2)、将条形统计图补充完整;(3)、若该校共有3000名学生,估计该校表示“喜欢”的B类学生大约有多少人?20. 如图,矩形ABCD的对角线AC、BD交于点O,且DE∥AC,CE∥BD.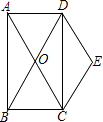 (1)、求证:四边形OCED是菱形;(2)、若∠BAC=30°,AC=4,求菱形OCED的面积.21. 如图,小明所在的兴趣小组站在广场的 , 处,用一定高度的测角仪分别于 , 两处测得雕像顶部 的仰角分别为 , .已知 , 两点的距离为 ,雕像下的基座高度 为 ,求雕像 的高度.(精确到 , )
(1)、求证:四边形OCED是菱形;(2)、若∠BAC=30°,AC=4,求菱形OCED的面积.21. 如图,小明所在的兴趣小组站在广场的 , 处,用一定高度的测角仪分别于 , 两处测得雕像顶部 的仰角分别为 , .已知 , 两点的距离为 ,雕像下的基座高度 为 ,求雕像 的高度.(精确到 , ) 22. 如图, 内接于 , 为 直径,点 在 的延长线上,且 .
22. 如图, 内接于 , 为 直径,点 在 的延长线上,且 .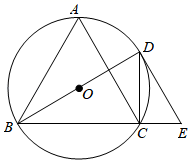 (1)、求证: 是 的切线;(2)、若 ,当 , 的半径为 ,则 的长为 .23. 如图,已知点 在 的负半轴上,点 在 的正半轴上, , ,点 在线段 上,从点 出发以每秒5单位长度的速度向点 运动,设运动时间为 秒,过点 作射线 轴于点 .
(1)、求证: 是 的切线;(2)、若 ,当 , 的半径为 ,则 的长为 .23. 如图,已知点 在 的负半轴上,点 在 的正半轴上, , ,点 在线段 上,从点 出发以每秒5单位长度的速度向点 运动,设运动时间为 秒,过点 作射线 轴于点 . (1)、当 时,线段 的长为(直接填空);(2)、当 时,求 的值;(3)、在射线 上取点 ,且始终满足 ,若 是以 为腰的等腰三角形,直接写出 的值.24. 已知:四边形 ,点 在直线 上,将 沿 翻折得到 ,点 的对应点 恰好落在直线 上,直线 交直线 于点 .
(1)、当 时,线段 的长为(直接填空);(2)、当 时,求 的值;(3)、在射线 上取点 ,且始终满足 ,若 是以 为腰的等腰三角形,直接写出 的值.24. 已知:四边形 ,点 在直线 上,将 沿 翻折得到 ,点 的对应点 恰好落在直线 上,直线 交直线 于点 . (1)、如图①,当四边形 为矩形时,
(1)、如图①,当四边形 为矩形时,①求证: ;
②若 , ,求线段 的长;
(2)、如图②,当四边形 为平行四边形时,若 ,直接写出此时 的值.25. 如图,在平面直角坐标系中,直线 与抛物线 交于点 和点 ,与 轴交于点 ,抛物线交 轴于点 ,点 是第一象限直线 上方抛物线上的一点,连接 , .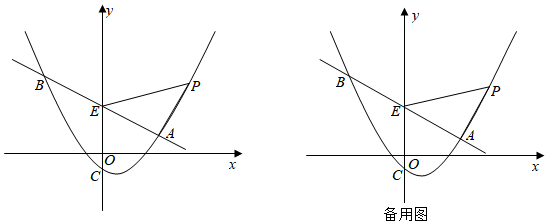 (1)、求抛物线的表达式;(2)、当 的面积等于 时,设点 的横坐标为 ,求 的值;(3)、将线段 绕点 顺时针旋转得到线段 ,旋转角为 ,连接 交线段 于点 , 的平分线交 于点 ,当 的周长最大时,直接写出点 的坐标.
(1)、求抛物线的表达式;(2)、当 的面积等于 时,设点 的横坐标为 ,求 的值;(3)、将线段 绕点 顺时针旋转得到线段 ,旋转角为 ,连接 交线段 于点 , 的平分线交 于点 ,当 的周长最大时,直接写出点 的坐标.