黑龙江省哈尔滨市平房区2021年中考数学二模试卷
试卷更新日期:2021-06-22 类型:中考模拟
一、单选题
-
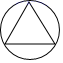
1. 下列各组数中互为相反数的是( )A、-2与 B、-2与 C、-2与 D、 与22. 下列运算中正确的是( )A、 B、 C、 D、3. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、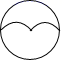 C、
C、 D、
D、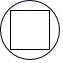 4. 已知反比例函数y= 的图象经过点(3a,a),则反比例函数的图象在( )A、在第一、二象限 B、在第一、三象限 C、在第二、四象限 D、在第三、四象限5. 如图是一个由5个相同的正方体组成的立体图形,它的主视图是( )
4. 已知反比例函数y= 的图象经过点(3a,a),则反比例函数的图象在( )A、在第一、二象限 B、在第一、三象限 C、在第二、四象限 D、在第三、四象限5. 如图是一个由5个相同的正方体组成的立体图形,它的主视图是( ) A、
A、 B、
B、 C、
C、 D、
D、 6. 如图,将 绕点A逆时针旋转得到 ,延长 交 于点D,若 ,则 的度数是( )
6. 如图,将 绕点A逆时针旋转得到 ,延长 交 于点D,若 ,则 的度数是( ) A、 B、 C、 D、7. 如图,在Rt△ABC中,∠ACB=90°,CD是AB边上的中线,AC=8,BC=6,则∠ACD的正切值是( )
A、 B、 C、 D、7. 如图,在Rt△ABC中,∠ACB=90°,CD是AB边上的中线,AC=8,BC=6,则∠ACD的正切值是( )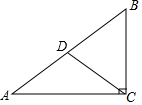 A、 B、 C、 D、8. 如图,在⊙O中,弦AB∥CD,连接BC,OA,OD.若∠BCD=20°,CD=OD,则∠AOD的度数是( )
A、 B、 C、 D、8. 如图,在⊙O中,弦AB∥CD,连接BC,OA,OD.若∠BCD=20°,CD=OD,则∠AOD的度数是( )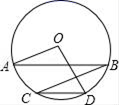 A、120° B、140° C、110° D、100°9. 一个盒子装有红、黄、白球分别为2、3、5个,这些球除颜色外都相同,从袋中任抽一个球,则抽到黄球的概率是( )A、 B、 C、 D、10. 如图,在 中,点D,E分别为AB,AC边上的点,且 ,CD、BE相较于点O,连接AO并延长交DE于点G,交BC边于点F,则下列结论中一定正确的是
A、120° B、140° C、110° D、100°9. 一个盒子装有红、黄、白球分别为2、3、5个,这些球除颜色外都相同,从袋中任抽一个球,则抽到黄球的概率是( )A、 B、 C、 D、10. 如图,在 中,点D,E分别为AB,AC边上的点,且 ,CD、BE相较于点O,连接AO并延长交DE于点G,交BC边于点F,则下列结论中一定正确的是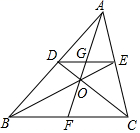 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
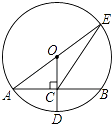
11. 一种植物果实像一个微笑的无花果,质量只有0.000000076克,该质量请用科学记数法表示克.12. 在函数 中,自变量x的取值范围是 .13. 分解因式: .14. 不等式组 的整数解的个数是 .15. 若关于x的方程 的解为正数,则m的取值范围是.16. 抛物线 的顶点坐标为 .17. 一个扇形的半径为 ,面积为 ,则此扇形的圆心角为 .18. 纸片 中, ,将它折叠使 与 重合,折痕 交 于点 ,则线段 的长为 .19. 如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,CD=2,则EC的长为 .
 20. 如图,在 中, , 分别在边 上, , ,则线段 的长为 .
20. 如图,在 中, , 分别在边 上, , ,则线段 的长为 .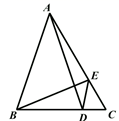
三、解答题
-
21. 先化简,再求值: ,其中m=tan60°- .22. 如图,在7×7的正方形网格中,每个小正方形的边长均为1,线段AB的端点均在小正方形的格点上(小正方形的顶点称为格点).
 (1)、在图中画一个Rt△ABC,使其同时满足以下三个条件:①A为直角顶点;②点C在格点上;③tan∠ACB= ;(2)、在(1)的条件下,请在网格中找到另一个格点D,满足tan∠CBD=1,连接CD,求线段CD的长.23. 微信圈有篇热传的文章《如果想毁掉一个孩子,就给他一部手机》.为了解学生手机使用情况,西安高新区某学校开展了“手机伴我健康行”的主题活动,学校随机抽取部分学生进行“使用手机目的”和“每周使用手机的时间”的问卷调查(问卷中的问题均为单项选择),并绘制①②统计图,在这次调查的学生中,手机使用目的为“玩游戏”的人数是35人.
(1)、在图中画一个Rt△ABC,使其同时满足以下三个条件:①A为直角顶点;②点C在格点上;③tan∠ACB= ;(2)、在(1)的条件下,请在网格中找到另一个格点D,满足tan∠CBD=1,连接CD,求线段CD的长.23. 微信圈有篇热传的文章《如果想毁掉一个孩子,就给他一部手机》.为了解学生手机使用情况,西安高新区某学校开展了“手机伴我健康行”的主题活动,学校随机抽取部分学生进行“使用手机目的”和“每周使用手机的时间”的问卷调查(问卷中的问题均为单项选择),并绘制①②统计图,在这次调查的学生中,手机使用目的为“玩游戏”的人数是35人.
请根据以上信息,解答下列问题:
(1)、在这次活动中被调查的学生共人;所抽取的学生使用手机时间的中位数落在范围内;(2)、补全条形统计图;(3)、该校共有学生4800人,请估算每周使用手机时间在2小时以上(不含2小时)的人数.24. 已知:在△ABC中,∠ACB=90°,点D,E分别为BC,AB的中点,连接DE,CE,点F在DE的延长线上,连接AF,且AF=AE.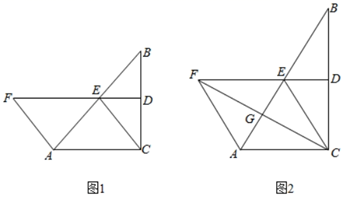 (1)、如图1,求证:四边形ACEF是平行四边形;(2)、如图2,当∠B=30°时,连接CF交AB于点G,在不添加任何辅助线的情况下,请直接写出图2中的四条线段,使每条线段的长度都等于线段DE的长度的 倍.25. 倡导健康生活推进全民健身,某社区去年购进A,B两种健身器材若干件,经了解,B种健身器材的单价是A种健身器材的1.5倍,用7200元购买A种健身器材比用5400元购买B种健身器材多10件.(1)、A,B两种健身器材的单价分别是多少元?(2)、若今年两种健身器材的单价和去年保持不变,该社区计划再购进A,B两种健身器材共50件,且费用不超过21000元,请问:A种健身器材至少要购买多少件?26. 已知 内接于圆 ,点 为弧 上一点,连接 交 于点 , .
(1)、如图1,求证:四边形ACEF是平行四边形;(2)、如图2,当∠B=30°时,连接CF交AB于点G,在不添加任何辅助线的情况下,请直接写出图2中的四条线段,使每条线段的长度都等于线段DE的长度的 倍.25. 倡导健康生活推进全民健身,某社区去年购进A,B两种健身器材若干件,经了解,B种健身器材的单价是A种健身器材的1.5倍,用7200元购买A种健身器材比用5400元购买B种健身器材多10件.(1)、A,B两种健身器材的单价分别是多少元?(2)、若今年两种健身器材的单价和去年保持不变,该社区计划再购进A,B两种健身器材共50件,且费用不超过21000元,请问:A种健身器材至少要购买多少件?26. 已知 内接于圆 ,点 为弧 上一点,连接 交 于点 , .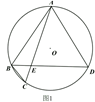
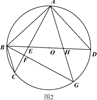
 (1)、如图1,求证:弧 弧 ;(2)、如图2,过 作 于点 ,交圆 点 ,连接 交 于点 ,且 ,求 的度数;(3)、如图3,在(2)的条件下,圆 上一点 与点 关于 对称,连接 ,交 于点 ,点 为弧 上一点, 交 于点 ,交 的延长线于点 , , 的周长为20, ,求圆 半径.27. 在平面直角坐标系中, 为坐标原点直线 与 轴交于点 ,与 轴交于点 , , 的面积为2.
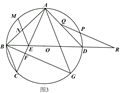
(1)、如图1,求证:弧 弧 ;(2)、如图2,过 作 于点 ,交圆 点 ,连接 交 于点 ,且 ,求 的度数;(3)、如图3,在(2)的条件下,圆 上一点 与点 关于 对称,连接 ,交 于点 ,点 为弧 上一点, 交 于点 ,交 的延长线于点 , , 的周长为20, ,求圆 半径.27. 在平面直角坐标系中, 为坐标原点直线 与 轴交于点 ,与 轴交于点 , , 的面积为2.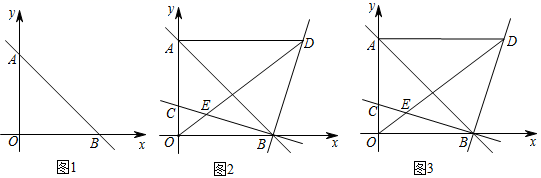 (1)、如图1,求直线 的解析式;(2)、如图2,线段 上有一点 ,直线 为 , 轴,将 绕点 顺时针旋转 ,交 于点 ,求点 的坐标.(用含 的式子表示)(3)、如图3,在(2)的条件下,连接 ,交直线 于点 ,若 ,求点 的坐标.
(1)、如图1,求直线 的解析式;(2)、如图2,线段 上有一点 ,直线 为 , 轴,将 绕点 顺时针旋转 ,交 于点 ,求点 的坐标.(用含 的式子表示)(3)、如图3,在(2)的条件下,连接 ,交直线 于点 ,若 ,求点 的坐标.