河北省玉田县2021年中考数学二模试卷
试卷更新日期:2021-06-22 类型:中考模拟
一、单选题
-
1. 如果a与b互为相反数,下列各式中错误的是( )A、 B、 C、 D、2. 如图1,该几何体是由5个棱长为1个单位长度的正方体摆放而成,将正方体A两次平移后所得的几何体如图2,下列关于视图的说法正确的是( )
 A、主视图改变,俯视图改变 B、主视图不变,俯视图不变 C、主视图改变,俯视图不变 D、主视图不变,俯视图改变3. 下列运算正确的是( )A、 B、 C、 D、4. 如图,现将一块三角板含有 角的顶点放在直尺的一边上,若 ,那么 的度数为( )
A、主视图改变,俯视图改变 B、主视图不变,俯视图不变 C、主视图改变,俯视图不变 D、主视图不变,俯视图改变3. 下列运算正确的是( )A、 B、 C、 D、4. 如图,现将一块三角板含有 角的顶点放在直尺的一边上,若 ,那么 的度数为( )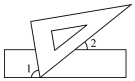 A、 B、 C、 D、5. 已知点 关于原点对称的点在第二象限,则a的取值范围在数轴上表示( )A、
A、 B、 C、 D、5. 已知点 关于原点对称的点在第二象限,则a的取值范围在数轴上表示( )A、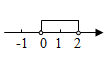 B、
B、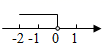 C、
C、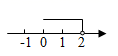 D、
D、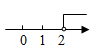 6. 如图, 是等边 的中线,点E在 上, ,则 的度数为( )
6. 如图, 是等边 的中线,点E在 上, ,则 的度数为( )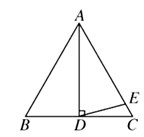 A、 B、 C、 D、7. 一名射箭运动员统计了45次射箭的成绩,并绘制了如图所示的折线统计图则在射箭成绩的这组数据中,众数和中位数分别是( )
A、 B、 C、 D、7. 一名射箭运动员统计了45次射箭的成绩,并绘制了如图所示的折线统计图则在射箭成绩的这组数据中,众数和中位数分别是( ) A、18,8 B、8,8 C、8,9 D、18,188. 如图,已知△ABC与△DEF位似,位似中心为点O,且AB:DE=3:2,则△ABC的面积与△DEF面积之比为( )
A、18,8 B、8,8 C、8,9 D、18,188. 如图,已知△ABC与△DEF位似,位似中心为点O,且AB:DE=3:2,则△ABC的面积与△DEF面积之比为( )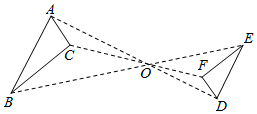 A、3:2 B、3:5 C、9:4 D、9:59. 我国北斗公司在2020年发布了一款代表国内卫星导航系统最高水平的芯片,该芯片的制造工艺达到了 米,用科学记数法表示 为( )A、 B、 C、 D、10. 如图,在平面直角坐标系中,函数 与 的图像交于点 ,则代数式 的值为( )
A、3:2 B、3:5 C、9:4 D、9:59. 我国北斗公司在2020年发布了一款代表国内卫星导航系统最高水平的芯片,该芯片的制造工艺达到了 米,用科学记数法表示 为( )A、 B、 C、 D、10. 如图,在平面直角坐标系中,函数 与 的图像交于点 ,则代数式 的值为( )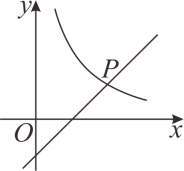 A、 B、 C、 D、11. 如图,有公共顶点O的两个边长为3的正五边形(不重叠),以O点为圆心,半径为3作圆,构成一个“蘑菇”形图案,则这个“蘑菇”形图案(阴影部分)的面积为( )
A、 B、 C、 D、11. 如图,有公共顶点O的两个边长为3的正五边形(不重叠),以O点为圆心,半径为3作圆,构成一个“蘑菇”形图案,则这个“蘑菇”形图案(阴影部分)的面积为( )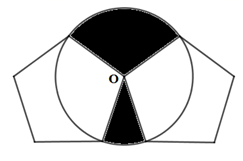 A、 B、 C、 D、12. 图1是一个地铁站入口的双翼闸机.如图2,它的双翼展开时,双翼边缘的端点A与B之间的距离为10cm,双翼的边缘AC=BD=54cm,且与闸机侧立面夹角∠PCA=∠BDQ=30°.当双翼收起时,可以通过闸机的物体的最大宽度为( )
A、 B、 C、 D、12. 图1是一个地铁站入口的双翼闸机.如图2,它的双翼展开时,双翼边缘的端点A与B之间的距离为10cm,双翼的边缘AC=BD=54cm,且与闸机侧立面夹角∠PCA=∠BDQ=30°.当双翼收起时,可以通过闸机的物体的最大宽度为( )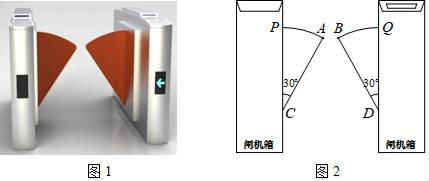 A、(54 +10) cm B、(54 +10) cm C、64 cm D、54cm13. 已知数据划x1、x2、x3、……、x100是福建某企业普通职工的2020年的年收入,设这100个数据的平均数为a,中位数为b,方差为c,如果再加上中国首富马化腾的年收入x101 , 则在这101个数据中,a一定增大,那么对b与c的判断正确的是( )A、b一定增大,c可能增大 B、b可能不变,c一定增大 C、b一定不变,c一定增大 D、b可能增大,c可能不变14. 如图,点O为等边三角形ABC的外心,四边形OCDE为正方形,其中E点在△ABC的外部,下列三角形中,外心不是点O的是( )
A、(54 +10) cm B、(54 +10) cm C、64 cm D、54cm13. 已知数据划x1、x2、x3、……、x100是福建某企业普通职工的2020年的年收入,设这100个数据的平均数为a,中位数为b,方差为c,如果再加上中国首富马化腾的年收入x101 , 则在这101个数据中,a一定增大,那么对b与c的判断正确的是( )A、b一定增大,c可能增大 B、b可能不变,c一定增大 C、b一定不变,c一定增大 D、b可能增大,c可能不变14. 如图,点O为等边三角形ABC的外心,四边形OCDE为正方形,其中E点在△ABC的外部,下列三角形中,外心不是点O的是( )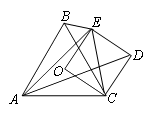 A、△CBE B、△ACD C、△ABE D、△ACE15. 如图,在3×4的正方形网格图中,小正方形的边长为1, 的顶点均在格点上,则下列关于 的说法错误的是( )
A、△CBE B、△ACD C、△ABE D、△ACE15. 如图,在3×4的正方形网格图中,小正方形的边长为1, 的顶点均在格点上,则下列关于 的说法错误的是( )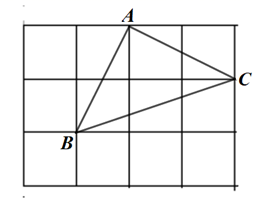 A、是直角三角形 B、 C、面积为4 D、 边上的高为16. 如图1,矩形的一条边长为x,周长的一半为y,定义(x,y)为这个矩形的坐标.如图2,在平面直角坐标系中,直线x=1,y=3将第一象限划分成4个区域,已知矩形1的坐标的对应点A落在如图所示的双曲线上,矩形2的坐标的对应点落在区域④中,则下面叙述中正确的是( )
A、是直角三角形 B、 C、面积为4 D、 边上的高为16. 如图1,矩形的一条边长为x,周长的一半为y,定义(x,y)为这个矩形的坐标.如图2,在平面直角坐标系中,直线x=1,y=3将第一象限划分成4个区域,已知矩形1的坐标的对应点A落在如图所示的双曲线上,矩形2的坐标的对应点落在区域④中,则下面叙述中正确的是( )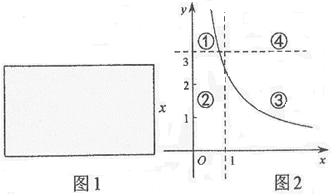 A、点A的横坐标有可能大于3 B、矩形1是正方形时,点A位于区域② C、当点A沿双曲线向上移动时,矩形1的面积减小 D、当点A位于区域①时,矩形1可能和矩形2全等
A、点A的横坐标有可能大于3 B、矩形1是正方形时,点A位于区域② C、当点A沿双曲线向上移动时,矩形1的面积减小 D、当点A位于区域①时,矩形1可能和矩形2全等二、填空题
-
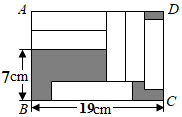
17. 分解因式: = .18. 如图,在长方形 中,放入6个形状、大小都相同的长方形,所标尺寸如图所示,则图中阴影部分面积是 , 若平移这六个长方形,则图中剩余的阴影部分面积是否改变?(填“变”或“不变”).
 19. 如图, ,点P为射线OM上一定点,且 ,点Q是射线 上一动点,且点Q以每秒2个单位长度的速度向右运动,设运动时间为t.连接 ,以 为一条边向右侧作等边 .若 ,则 ;若t的取值范围是 ,则点H的运动路径长为 .
19. 如图, ,点P为射线OM上一定点,且 ,点Q是射线 上一动点,且点Q以每秒2个单位长度的速度向右运动,设运动时间为t.连接 ,以 为一条边向右侧作等边 .若 ,则 ;若t的取值范围是 ,则点H的运动路径长为 .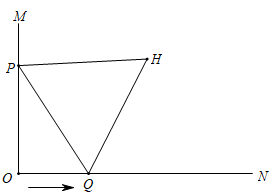
三、解答题
-
20. 如图,数轴上有A、B、C三个点,它们所表示的数分别为a、b、c三个数,其中 ,且b的倒数是它本身,且a、c满足 .
 (1)、计算: 的值;(2)、若将数轴折叠,使得点A与点B重合,求与点C重合的点表示的数.21. 下面是嘉琪同学设计的“过直线外一点作已知直线的平行线”的尺规作图过程.
(1)、计算: 的值;(2)、若将数轴折叠,使得点A与点B重合,求与点C重合的点表示的数.21. 下面是嘉琪同学设计的“过直线外一点作已知直线的平行线”的尺规作图过程.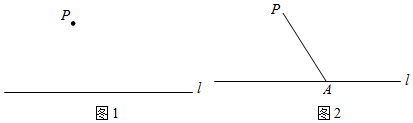
已知:如图1,直线l和直线l外一点P.
求作:直线 ,使直线 直线l.
作法:如图2,
①在直线l上取一点A,连接 ;
②作 的垂直平分线 ,分别交直线l,线段 于点B,O;
③以O为圆心, 长为半径作弧,交直线 于另一点Q;
④作直线 ,所以直线 为所求作的直线.
根据上述作图过程,回答问题:
(1)、用直尺和圆规,补全图2中的图形(保留作图痕迹);(2)、完成下面的证明:证明:∵直线 是 的垂直平分线,
∴ ▲ = ▲ , .
∵ ▲ = ▲ ,
∴ .
∴ ▲ = ▲ .
∴ ( ▲ )(填推理的依据).
22. 在甲、乙两个不透明的口袋中,分别有大小、材质完全相同的小球,其中甲口袋中的小球上分别标有数字2,3,4,5,乙口袋中的小球上分别标有数字3,4,5,琪琪先从甲袋中任意摸出一个小球,记下数字为m,乐乐从乙袋中任意摸出一个小球,记下数字为n.(1)、从甲袋摸出一个小球,则小球上的数字使代数式 的值为0的概率;(2)、若m,n都是方程 的解时,则琪琪获胜;若m,n都不是方程 的解时,则乐乐获胜;问他们两人谁获胜的概率大.23. 如图,在平面直角坐标系中,已知二次函数 图象的顶点为A,与y轴交于点B,异于顶点A的点C(1,n)在该函数图象上. (1)、当m=5时,求n的值.(2)、当n=2时,若点A在第一象限内,结合图象,求当y 时,自变量x的取值范围.(3)、作直线AC与y轴相交于点D.当点B在x轴上方,且在线段OD上时,求m的取值范围.24. 某超市一段时期内对某种商品经销情况进行统计分析:得到该商品的销售数量 (件)由基础销售量与浮动销售量两个部分组成,其中基本销售量保持不变,浮动销售量与售价 (元/件, )成反比例,销售过程中得到的部分数据如下:
(1)、当m=5时,求n的值.(2)、当n=2时,若点A在第一象限内,结合图象,求当y 时,自变量x的取值范围.(3)、作直线AC与y轴相交于点D.当点B在x轴上方,且在线段OD上时,求m的取值范围.24. 某超市一段时期内对某种商品经销情况进行统计分析:得到该商品的销售数量 (件)由基础销售量与浮动销售量两个部分组成,其中基本销售量保持不变,浮动销售量与售价 (元/件, )成反比例,销售过程中得到的部分数据如下:售价
8
10
销售数量
70
58
(1)、求 与 之间的函数关系式;(2)、当该商品销售数量为50件时,求每件商品的售价;(3)、设销售总额为 ,求 的最大值.25. 如图,在 中, ,以点O为圆心、2为半径画圆,过点A作 的切线,切点为P , 连接 .将 绕点O按逆时针方向旋转到 时,连接 .设旋转角为 .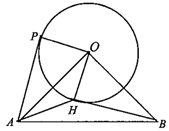 (1)、当 时,求证: 是 的切线;(2)、当 与 相切时,求旋转角 和点H运动路径的长;(3)、当 面积最大时,请直接写出此时点H到 的距离.26. 如图,在矩形ABCD中,AB=8,BC=12,点E在AB上,AE=5,P是AD上一点,将矩形沿PE折叠,点A落在点 处.连接AC , 与PE相交于点F , 设AP=x .
(1)、当 时,求证: 是 的切线;(2)、当 与 相切时,求旋转角 和点H运动路径的长;(3)、当 面积最大时,请直接写出此时点H到 的距离.26. 如图,在矩形ABCD中,AB=8,BC=12,点E在AB上,AE=5,P是AD上一点,将矩形沿PE折叠,点A落在点 处.连接AC , 与PE相交于点F , 设AP=x .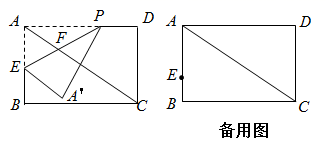 (1)、AC=;(2)、若点 在∠BAC的平分线上,求FC的长;(3)、求点 ,D距离的最小值,并求此时tan∠APE的值;(4)、若点 在△ABC的内部,直接写出x的取值范围.
(1)、AC=;(2)、若点 在∠BAC的平分线上,求FC的长;(3)、求点 ,D距离的最小值,并求此时tan∠APE的值;(4)、若点 在△ABC的内部,直接写出x的取值范围.