河北省唐山市迁西县2021年中考数学模拟试卷
试卷更新日期:2021-06-22 类型:中考模拟
一、单选题
-
1. 数 中最大的是( )A、1 B、-3 C、 D、02. 如图,在 中, ,则 的值为( )
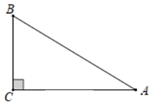 A、 B、1 C、 D、3. 用科学记数法表示数字160531(精确到千位)是( )A、 B、 C、 D、4. 下面的多边形中,内角和与外角和相等的是( )A、
A、 B、1 C、 D、3. 用科学记数法表示数字160531(精确到千位)是( )A、 B、 C、 D、4. 下面的多边形中,内角和与外角和相等的是( )A、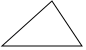 B、
B、 C、
C、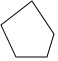 D、
D、 5. 下列式子错误的是( )A、 B、 C、 D、6. 如图, ,下列说法错误的是( )
5. 下列式子错误的是( )A、 B、 C、 D、6. 如图, ,下列说法错误的是( ) A、两个三角形是位似图形 B、点A是两个三角形的位似中心 C、点B与点 D、点C与点E是对应位似点 D. 是相似比7. 已知 ,则化简代数式 的结果是( )A、 B、 C、 D、8. 如图,已知:直线AB和AB外一点C,用尺规作AB的垂线,使它经过点C.步骤如下:
A、两个三角形是位似图形 B、点A是两个三角形的位似中心 C、点B与点 D、点C与点E是对应位似点 D. 是相似比7. 已知 ,则化简代数式 的结果是( )A、 B、 C、 D、8. 如图,已知:直线AB和AB外一点C,用尺规作AB的垂线,使它经过点C.步骤如下:⑴任意取一点K.
⑵以点C为圆心,CK长为半径作弧,交AB于点D和E.
⑶分别以点D和点E为圆心,以a长为半径作弧,两弧相交于点F.
⑷作直线CF,直线CF就是所求作的垂线.下列正确的是( )
 A、对点K,a长无要求 B、点K与点C在AB同侧,a≥ DE C、点K与点C在AB异侧,a> DE D、点K与点C在AB同侧,a< DE9. 如图,数轴上点C所表示的数是( )
A、对点K,a长无要求 B、点K与点C在AB同侧,a≥ DE C、点K与点C在AB异侧,a> DE D、点K与点C在AB同侧,a< DE9. 如图,数轴上点C所表示的数是( ) A、 B、 C、3.6 D、3.710. 如图, 与 交于点 ,则 ( )
A、 B、 C、3.6 D、3.710. 如图, 与 交于点 ,则 ( ) A、2 B、3 C、3.5 D、411. 若 ,则 的值为( )A、-2 B、2 C、-4 D、412. 一个小球在如图所示的地板上自由滚动,并随机停在某块方砖上.如果每一块方砖除颜色外完全相同,那么小球最终停留在黑砖上的概率是( )
A、2 B、3 C、3.5 D、411. 若 ,则 的值为( )A、-2 B、2 C、-4 D、412. 一个小球在如图所示的地板上自由滚动,并随机停在某块方砖上.如果每一块方砖除颜色外完全相同,那么小球最终停留在黑砖上的概率是( ) A、 B、 C、 D、113. 如图,快艇从 地出发,要到距离 地10海里的 地去,先沿北偏东70°方向走了8海里,到达 地,然后再从 地走了6海里到达 地,此时快艇位于 地的( ).
A、 B、 C、 D、113. 如图,快艇从 地出发,要到距离 地10海里的 地去,先沿北偏东70°方向走了8海里,到达 地,然后再从 地走了6海里到达 地,此时快艇位于 地的( ). A、北偏东20°方向上 B、北偏西20°方向上 C、北偏西30°方向上 D、北偏西40°方向上14. 如图是某个球放进盒子内的截面图,球的一部分露出盒子外,已知⊙O交矩形ABCD的边AD于点E,F,已知AB=EF=2,则球的半径长为( )
A、北偏东20°方向上 B、北偏西20°方向上 C、北偏西30°方向上 D、北偏西40°方向上14. 如图是某个球放进盒子内的截面图,球的一部分露出盒子外,已知⊙O交矩形ABCD的边AD于点E,F,已知AB=EF=2,则球的半径长为( ) A、 B、 C、 D、15. 如图,抛物线 与x轴交于点 ,把抛物线在x轴及其下方的部分记作 ,将 向左平移得到 与x轴交于点 ,若直线 与 共有3个不同的交点,则m的取值范围是( )
A、 B、 C、 D、15. 如图,抛物线 与x轴交于点 ,把抛物线在x轴及其下方的部分记作 ,将 向左平移得到 与x轴交于点 ,若直线 与 共有3个不同的交点,则m的取值范围是( ) A、 B、 C、 D、16. 如图,半圆O的直径 ,将半圆O绕点B顺针旋转 得到半圆 ,与AB交于点P,则图中阴影部分的面积为( )
A、 B、 C、 D、16. 如图,半圆O的直径 ,将半圆O绕点B顺针旋转 得到半圆 ,与AB交于点P,则图中阴影部分的面积为( ) A、 B、 C、8π D、
A、 B、 C、8π D、二、填空题
-
17. 化简: .18. 如图,将长为 ,宽为 的长方形 先向右平移 ,再向下平移 ,得到长方形 ,则阴影部分的面积为 .
 19. 如图所示,双曲线 上有一动点A,连接 ,以O为顶点、 为直角边,构造等腰直角角形 ,则 面积的最小值为 . 此时A点坐标为 .
19. 如图所示,双曲线 上有一动点A,连接 ,以O为顶点、 为直角边,构造等腰直角角形 ,则 面积的最小值为 . 此时A点坐标为 .
三、解答题
-
20. 如图是一个正方体纸盒的表面展开图,纸盒中相对两个面上的数互为相反数.
-3
2
a
c
b
-1
(1)、填空: , , ;(2)、将 化简,并代入求值.21. 解密数学魔术:魔术师请观众心想一个数a,然后将这个数按以下步骤操作: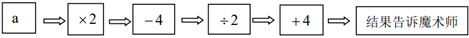
魔术师能立刻说出观众想的那个数.
(1)、如果小明想的数是-1,那么她告诉魔术师的结果应该是;(2)、如果小明想了一个数计算后,告诉魔术师结果为42,那么魔术师立刻说出小明想的那个数是;(3)、观众又进行了几次尝试,魔术师都能立刻说出他们想的那个数.请通过计算说明这个魔术的奥妙.22. 已知:如图,在 中, 为边 上一点,以 为邻边作平行四边形 ,连接 . (1)、求证: ;(2)、求证: ;(3)、当点 在什么位置时,四边形 是矩形,请说明理由.23. 某初级中学数学兴趣小组为了了解本校学生的年龄情况,随机调查了该校部分学生的年龄,整理数据并绘制如下不完整的统计图.
(1)、求证: ;(2)、求证: ;(3)、当点 在什么位置时,四边形 是矩形,请说明理由.23. 某初级中学数学兴趣小组为了了解本校学生的年龄情况,随机调查了该校部分学生的年龄,整理数据并绘制如下不完整的统计图.
依据以上信息解答以下问题:
(1)、求样本容量,并补全条形统计图;(2)、直接写出样本的平均数,众数和中位数;(3)、若该校一共有900名学生,估计该校年龄在13岁及以下的学生人数.24. 如图,已知直线l1 , 经过点B(0,3)、点C(2,﹣3),交x轴于点D,点P是x轴上一个动点,过点C、P作直线l2 . (1)、求直线l1的表达式;(2)、已知点A(7,0),当S△DPC= S△ACD时,求点P的坐标;(3)、设点P的横坐标为m,点M(x1 , y1),N(x2 , y2)是直线l2上任意两个点,若x1>x2时,有y1<y2 , 请直接写出m的取值范围.25. 如图, 为 的外接圆, ,点D是 上的动点,且点 分别位于 的两侧.
(1)、求直线l1的表达式;(2)、已知点A(7,0),当S△DPC= S△ACD时,求点P的坐标;(3)、设点P的横坐标为m,点M(x1 , y1),N(x2 , y2)是直线l2上任意两个点,若x1>x2时,有y1<y2 , 请直接写出m的取值范围.25. 如图, 为 的外接圆, ,点D是 上的动点,且点 分别位于 的两侧. (1)、求 的半径;(2)、当 时,求 的度数;(3)、设 的中点为M,在点D的运动过程中,线段 是否存在最大值?若存在,求出 的最大值;若不存在,请说明理由.26. 某小区发现一名新型冠状病毒无症状感染者,政府决定对该小区所有居民进行核酸检测.从上午 起第x分钟等候检测的居民人数为y人,且y与x成二次函数关系(如图所示),已知在第10分钟时,等候检测的人数达到最大值150人.
(1)、求 的半径;(2)、当 时,求 的度数;(3)、设 的中点为M,在点D的运动过程中,线段 是否存在最大值?若存在,求出 的最大值;若不存在,请说明理由.26. 某小区发现一名新型冠状病毒无症状感染者,政府决定对该小区所有居民进行核酸检测.从上午 起第x分钟等候检测的居民人数为y人,且y与x成二次函数关系(如图所示),已知在第10分钟时,等候检测的人数达到最大值150人. (1)、求 分钟内,y与x的函数解析式并写出此二次函数中的 的值.(2)、若 起检测人员开始工作,共设两个检测岗,已知每岗每分钟可让检测完毕的5个居民离开,问检测开始后,
(1)、求 分钟内,y与x的函数解析式并写出此二次函数中的 的值.(2)、若 起检测人员开始工作,共设两个检测岗,已知每岗每分钟可让检测完毕的5个居民离开,问检测开始后,①第几分钟等候检测的居民人数最多,是多少人?
②第几分钟时等候检测的居民人数是0.