河北省邯郸市2021年中考数学三模试卷
试卷更新日期:2021-06-22 类型:中考模拟
一、单选题
-
1. 下列倡导节约的图案中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 把 写成 ( , 为整数)的形式,则 为( )A、2.58 B、5.58 C、-0.58 D、-0.423. 如图是某个几何体的三视图,该几何体是( )
2. 把 写成 ( , 为整数)的形式,则 为( )A、2.58 B、5.58 C、-0.58 D、-0.423. 如图是某个几何体的三视图,该几何体是( ) A、圆锥 B、三棱柱 C、圆柱 D、三棱锥4. 下列各数中,负数是( )A、 B、 C、 D、5. 当压力F(N)一定时,物体所受的压强p(Pa)与受力面积S(m2)的函数关系式为P= (S≠0),这个函数的图象大致是( )A、
A、圆锥 B、三棱柱 C、圆柱 D、三棱锥4. 下列各数中,负数是( )A、 B、 C、 D、5. 当压力F(N)一定时,物体所受的压强p(Pa)与受力面积S(m2)的函数关系式为P= (S≠0),这个函数的图象大致是( )A、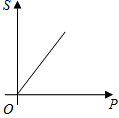 B、
B、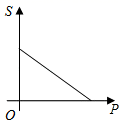 C、
C、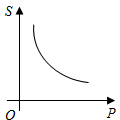 D、
D、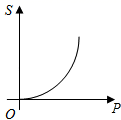 6. 如图,现将一块三角板含有 角的顶点放在直尺的一边上,若 ,那么 的度数为( )
6. 如图,现将一块三角板含有 角的顶点放在直尺的一边上,若 ,那么 的度数为( )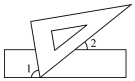 A、 B、 C、 D、7. 下列运算正确的是( )A、 B、 C、 D、8. 如图,若 与 是位似图形,则位似中心可能是( )
A、 B、 C、 D、7. 下列运算正确的是( )A、 B、 C、 D、8. 如图,若 与 是位似图形,则位似中心可能是( ) A、 B、 C、 D、9. 的计算结果是( )A、0 B、-2 C、1 D、210. 如图,甲、乙两船同时从港口O出发,其中甲船沿北偏西30°方向航行,乙船沿南偏西70°方向航行,已知两船的航行速度相同,如果1小时后甲、乙两船分别到达点A、B处,那么点B位于点A的( )
A、 B、 C、 D、9. 的计算结果是( )A、0 B、-2 C、1 D、210. 如图,甲、乙两船同时从港口O出发,其中甲船沿北偏西30°方向航行,乙船沿南偏西70°方向航行,已知两船的航行速度相同,如果1小时后甲、乙两船分别到达点A、B处,那么点B位于点A的( ) A、南偏西40° B、南偏西30° C、南偏西20° D、南偏西10°11. 如图是解不等式 的过程,每一步只对上一步负责,则其中有错的步骤是( )
A、南偏西40° B、南偏西30° C、南偏西20° D、南偏西10°11. 如图是解不等式 的过程,每一步只对上一步负责,则其中有错的步骤是( )解:∵ ,
∴ ,①
∴ ,②
∴ ,③
∴ .④
A、只有④ B、①③ C、②④ D、①②④12. 如图是某厂家新开发的一款摩托车,它的大灯射出的光线 , 与地面 的夹角分别为8°和10°,该大灯照亮地面的宽度 的长为3.5米,则该大灯距地面的高度为( )(参考数据: , , , )
 A、3.5米 B、2.5米 C、4.5米 D、5.5米13. 若 ,则( )中的数是( )A、-1 B、1 C、-2 D、任意实数14. 如图,已知 的顶点 , 分别在 轴, 轴上, , ,按以下步骤作图:①分别以点 , 为圆心,大于 的长为半径作弧,交于点 , ;②作直线 交 轴于点 ,交 轴于点 ,则点 的坐标为( )
A、3.5米 B、2.5米 C、4.5米 D、5.5米13. 若 ,则( )中的数是( )A、-1 B、1 C、-2 D、任意实数14. 如图,已知 的顶点 , 分别在 轴, 轴上, , ,按以下步骤作图:①分别以点 , 为圆心,大于 的长为半径作弧,交于点 , ;②作直线 交 轴于点 ,交 轴于点 ,则点 的坐标为( ) A、 B、 C、 D、15. 如图被称为“杨辉三角”或“贾宪三角”.其规律是:从第三行起,每行两端的数都是“1”,其余各数都等于该数“两肩”上的数之和.表中两平行线之间的一列数:1,3,6,10,15,…,我们把第一个数记为 ,第二个数记为 ,第三个数记为 ,…,第 个数记为 ,则 的值为( )
A、 B、 C、 D、15. 如图被称为“杨辉三角”或“贾宪三角”.其规律是:从第三行起,每行两端的数都是“1”,其余各数都等于该数“两肩”上的数之和.表中两平行线之间的一列数:1,3,6,10,15,…,我们把第一个数记为 ,第二个数记为 ,第三个数记为 ,…,第 个数记为 ,则 的值为( ) A、76 B、74 C、72 D、7016. 现有一张纸片, , , .有甲、乙两种剪拼方案,如图1,2所示将它们沿着虚线剪开后,各自要拼一个与原来面积相等的正方形,则( )
A、76 B、74 C、72 D、7016. 现有一张纸片, , , .有甲、乙两种剪拼方案,如图1,2所示将它们沿着虚线剪开后,各自要拼一个与原来面积相等的正方形,则( )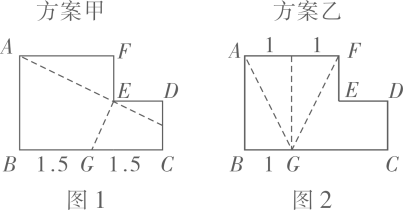 A、甲、乙都不可以 B、甲不可以、乙可以乙 C、甲、乙都可以 D、甲可以、乙不可以
A、甲、乙都不可以 B、甲不可以、乙可以乙 C、甲、乙都可以 D、甲可以、乙不可以二、填空题
-
17. 计算 的结果为 .18. 已知 ,则 .19. 在数学活动课中我们学习过平面镶嵌,若给出如图所示的一些边长均为1的正三角形、正六边形卡片,要求必须同时使用这两种卡片,不重叠、无缝隙,围绕某一个顶点拼在一起,成一个平面图案,则共拼出种不同的图案;其中所拼的图案中最大的周长为 .

三、解答题
-
20. 对于四个数“-8,-2,1,3”及四种运算“+,-,×,÷”,列算式解答:(1)、求这四个数的和;(2)、在这四个数中选出两个数,使得两数差的结果最小;(3)、在这四个数中选出三个数,在四种运算中选出两种,组成一个算式,可以带括号,使运算结果等于没选的那个数.21. 甲、乙两个长方形的边长如图所示( 为正整数),其面积分别为 , .
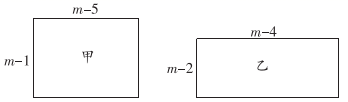 (1)、用含 的代数式表示出 和 ;(2)、比较 和 的大小, (用“>”“<”或“=”进行连接);(3)、若一个正方形的周长等于甲、乙两个长方形的周长之和,求该正方形的面积(用含 的代数式表示).22. 为落实我市关于开展中小学课后服务工作的要求,某学校开设了四门校本课程供学生选择:A . 趣味数学;B . 博乐阅读;C . 快乐英语;D . 硬笔书法.某年级共有100名学生选择了A课程,为了解本年级选择A课程学生的学习情况,从这100名学生中随机抽取了30名学生进行测试,将他们的成绩(百分制)分成六组,绘制成频数分布直方图.
(1)、用含 的代数式表示出 和 ;(2)、比较 和 的大小, (用“>”“<”或“=”进行连接);(3)、若一个正方形的周长等于甲、乙两个长方形的周长之和,求该正方形的面积(用含 的代数式表示).22. 为落实我市关于开展中小学课后服务工作的要求,某学校开设了四门校本课程供学生选择:A . 趣味数学;B . 博乐阅读;C . 快乐英语;D . 硬笔书法.某年级共有100名学生选择了A课程,为了解本年级选择A课程学生的学习情况,从这100名学生中随机抽取了30名学生进行测试,将他们的成绩(百分制)分成六组,绘制成频数分布直方图.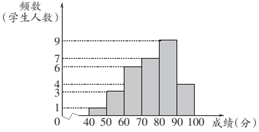 (1)、已知 这组的数据为:72,73,75,74,79,76,76,则这组数据的中位数是 , 众数是;(2)、根据题中信息,估计该年级选择A课程学生成绩在 的总人数;(3)、该年级每名学生选两门不同的课程,小张同时选择课程A和课程B的概率是多少?请用列表法或树状图的方法加以说明.23. 如图,点O在直线l上,过点O作 , .P为直线l上一点,连结 ,在直线l右侧取点B, ,且 ,过点B作 交l于点C.
(1)、已知 这组的数据为:72,73,75,74,79,76,76,则这组数据的中位数是 , 众数是;(2)、根据题中信息,估计该年级选择A课程学生成绩在 的总人数;(3)、该年级每名学生选两门不同的课程,小张同时选择课程A和课程B的概率是多少?请用列表法或树状图的方法加以说明.23. 如图,点O在直线l上,过点O作 , .P为直线l上一点,连结 ,在直线l右侧取点B, ,且 ,过点B作 交l于点C. (1)、求证: ;(2)、若 ,求 的长;(3)、连结 ,若点C为 的外心,则 .24. , , 三地在同一条公路上, 地在 , 两地之间,且与 , 两地的路程相等.甲、乙两车分别从 , 两地同时出发,匀速行驶.甲车到达 地停留1小时后以原速度继续前往 地,到达 地后立即调头(调头时间忽略不计),并按原路原速返回 地停止;乙车经C地到达 地停止,且比甲车早1小时到达 地.两车距 地的路程 ( )与所用时间 ( )的函数关系如图所示.请结合图象信息解答下列问题:
(1)、求证: ;(2)、若 ,求 的长;(3)、连结 ,若点C为 的外心,则 .24. , , 三地在同一条公路上, 地在 , 两地之间,且与 , 两地的路程相等.甲、乙两车分别从 , 两地同时出发,匀速行驶.甲车到达 地停留1小时后以原速度继续前往 地,到达 地后立即调头(调头时间忽略不计),并按原路原速返回 地停止;乙车经C地到达 地停止,且比甲车早1小时到达 地.两车距 地的路程 ( )与所用时间 ( )的函数关系如图所示.请结合图象信息解答下列问题: (1)、 , 两地的路程为 ,乙车的速度为 ;(2)、求图象中线段 所表示的 与 的函数解析式(不需要写出自变量 的取值范围);(3)、两车出发后经过多长时间相距 的路程?请直接写出答案.25. 在矩形 中, , ,点 从点 出发沿 边以 的速度向点 移动(点 可以与点 重合),同时,点 从点 出发沿 以 的速度向点 移动(点 可以与点 重合),其中一点到达终点时,另一点随之停止运动设运动时间为 秒.
(1)、 , 两地的路程为 ,乙车的速度为 ;(2)、求图象中线段 所表示的 与 的函数解析式(不需要写出自变量 的取值范围);(3)、两车出发后经过多长时间相距 的路程?请直接写出答案.25. 在矩形 中, , ,点 从点 出发沿 边以 的速度向点 移动(点 可以与点 重合),同时,点 从点 出发沿 以 的速度向点 移动(点 可以与点 重合),其中一点到达终点时,另一点随之停止运动设运动时间为 秒. (1)、如图1,几秒后, 的面积等于 ?(2)、如图2,在运动过程中,若以 为圆心、 为半径的 与 相切,求 值;(3)、若以 为圆心, 为半径作 .如图3,若 与四边形 的边有三个公共点,则 的取值范围为 . (直接写出结果,不需说理)26. 如图1,在平面直角坐标系 中,已知抛物线 : ( ).
(1)、如图1,几秒后, 的面积等于 ?(2)、如图2,在运动过程中,若以 为圆心、 为半径的 与 相切,求 值;(3)、若以 为圆心, 为半径作 .如图3,若 与四边形 的边有三个公共点,则 的取值范围为 . (直接写出结果,不需说理)26. 如图1,在平面直角坐标系 中,已知抛物线 : ( ). (1)、若抛物线过点 ,求出抛物线的解析式;(2)、当 时, 的最小值是 ,求 时, 的最大值;(3)、已知直线 与抛物线 ( )存在两个交点,若两交点到 轴的距离相等,求 的值;(4)、如图2,作与抛物线 关于 轴对称且对称轴相同的抛物线 ,当抛物线 与抛物线 围成的封闭区域内(不包括边界)共有11个横、纵坐标均为整数的点时,直接写出 的取值范围.
(1)、若抛物线过点 ,求出抛物线的解析式;(2)、当 时, 的最小值是 ,求 时, 的最大值;(3)、已知直线 与抛物线 ( )存在两个交点,若两交点到 轴的距离相等,求 的值;(4)、如图2,作与抛物线 关于 轴对称且对称轴相同的抛物线 ,当抛物线 与抛物线 围成的封闭区域内(不包括边界)共有11个横、纵坐标均为整数的点时,直接写出 的取值范围.