安徽省黄山市休宁县2021年中考数学模拟试卷
试卷更新日期:2021-06-22 类型:中考模拟
一、单选题
-
1. 下列四个数中,结果为负数的是( ).A、-1 B、|-1| C、(-1)2 D、-(-1)2. 计算 的结果为( )A、 B、 C、 D、3. 北京冬奥会和冬残奥会赛会志愿者招募工作进展顺利,截止 年底,赛会志愿者申请人数已突破 人.将 用科学记数法表示为( )A、 B、 C、 D、4. 下列几何体中,其主视图是圆的是( )A、
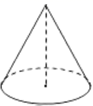 B、
B、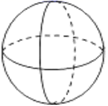 C、
C、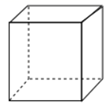 D、
D、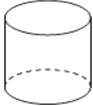 5. 不等式组 的解集是( )A、 B、 C、 或 D、6. 某口罩厂六月份的口罩产量为100万只,由于市场需求量减少,八月份的产量减少到81万只设该厂七八月份的口罩产量的月平均减少率为x,可列方程为( )A、 B、 C、 D、7. 某校为了解学生的课外阅读情况,随机抽取了一个班级的学生,对他们一周的读书时间进行了统计,统计数据如表所示:
5. 不等式组 的解集是( )A、 B、 C、 或 D、6. 某口罩厂六月份的口罩产量为100万只,由于市场需求量减少,八月份的产量减少到81万只设该厂七八月份的口罩产量的月平均减少率为x,可列方程为( )A、 B、 C、 D、7. 某校为了解学生的课外阅读情况,随机抽取了一个班级的学生,对他们一周的读书时间进行了统计,统计数据如表所示:读书时间(小时)
7
8
9
10
11
学生人数
6
10
9
8
7
关于该班学生一周读书时间的数据有下列说法:
①一周读书时间数据的中位数是9小时;
②一周读书时间数据的众数是8小时;
③一周读书时间数据的平均数是9小时;
④一周读书时间不少于9小时的人数占抽查学生的50%.
其中说法正确的个数有( )
A、1个 B、2个 C、3个 D、4个8. 如图,在半径1的圆形纸片中,剪一个圆心角为90°的扇形(图中阴影部分),则这个扇形的面积为( )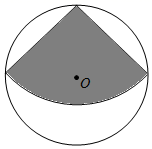 A、 B、 C、 D、9. 如图,一块含有 的直角三角板的直角顶点和坐标原点 重合, 角的顶点 在反比例函数 的图象上,顶点 在反比例函数 的图象上,则 的值为( )
A、 B、 C、 D、9. 如图,一块含有 的直角三角板的直角顶点和坐标原点 重合, 角的顶点 在反比例函数 的图象上,顶点 在反比例函数 的图象上,则 的值为( ) A、12 B、-12 C、3 D、-310. 如图,在 中, ,点 是 边上一动点,过点 作 交 的延长线于 .若 , ,则 的最小值为( )
A、12 B、-12 C、3 D、-310. 如图,在 中, ,点 是 边上一动点,过点 作 交 的延长线于 .若 , ,则 的最小值为( ) A、 B、1 C、 D、
A、 B、1 C、 D、二、填空题
-
11. 4的算术平方根是 .12. 因式分解: .13. 如图,在平行四边形 中, 为 的中点, 为 上点, 交 于点 , , , ,则 的长为cm.
 14. 在平面直角坐标系 中, , ,若抛物线 经过点A且与线段AB有两个不同的交点,则a的取值范围是 .
14. 在平面直角坐标系 中, , ,若抛物线 经过点A且与线段AB有两个不同的交点,则a的取值范围是 .三、解答题
-
15. 计算: .16. 某数学兴趣小组研究我国古代《算法统宗》里这样一首诗:我间开店李三公,众客都来到店中,一房五客多五客,一房七客一房空诗中后两句的意思是:如果每一间客房住5人,那么有5人无房住:如果每一间客房住7人,那么就空出一间房.求该店有客房多少间?房客多少人?17. 如图,在平面直角坐标系中, 的顶点坐标分别为 , ,

( 1 )以原点O为位似中心, 在y轴的右侧画出将 放大为原来的2倍得到的 ,请写出点A的对应点 的坐标;
( 2 )画出将 向左平移2个单位, 再向上平移1个单位后得到的 ,写出点B的对应点 的坐标;
( 3 )请在图中标出 与 的位似中心M, 并写出点M的坐标.
18. 观察下列各式:① ;② ;③ ;④ .
根据上面三个式子所呈现的规律,完成下列各题:
(1)、写出第⑤个式子:;(2)、写出第 个式子( ,且 为整数),并给出证明.19. 知识改变世界,科技改变生活。导航装备的不断更新极大方便了人们的出行.如图,某校组织学生乘车到黑龙滩(用C表示)开展社会实践活动,车到达A地后,发现C地恰好在A地的正北方向,且距离A地13千米,导航显示车辆应沿北偏东60°方向行驶至B地,再沿北偏西37°方向行驶一段距离才能到达C地,求B、C两地的距离.(参考数据:sin53°≈ ,cos53°≈ ,tan53°≈ ) 20. 如图, 为 的直径, 是 上的一点,连接 , . 是 的中点,过 作 于点 ,交 于点 .
20. 如图, 为 的直径, 是 上的一点,连接 , . 是 的中点,过 作 于点 ,交 于点 . (1)、求证: ;(2)、若 , ,求 的长.21. 今年2~4月某市出现了400名新冠肺炎患者,市委根据党中央的决定,对患者进行了免费治疗,图1是该市轻症、重症、危重症三类患者的人数分布统计图(不完整),图2是这三类患者的人均治疗费用统计图.请回答下列问题.
(1)、求证: ;(2)、若 , ,求 的长.21. 今年2~4月某市出现了400名新冠肺炎患者,市委根据党中央的决定,对患者进行了免费治疗,图1是该市轻症、重症、危重症三类患者的人数分布统计图(不完整),图2是这三类患者的人均治疗费用统计图.请回答下列问题. (1)、轻症患者的人数是多少?(2)、所有患者的平均治疗费用是多少万元?(3)、由于部分轻症患者康复出院,为减少病房拥挤,拟对某病房中的 、 、 、 、 五位患者任选两位转入另一病房,请用树状图法或列表法求出恰好选中 、 两位患者的概率.22. 为了解交通拥堵情况,经统计分析,某高架桥上的车流速度 (千米小时)是车流密度 (辆千米)的函数,当桥上的车流密度达到220辆/千米时,造成堵塞,此时车流速度为0千米/小时;当车流密度为20辆/千米时,车流速度为80千米/小时,研究表明:当 时,车流速度 是车流密度 的一次函数.(1)、某高架桥上车流密度为100辆/千米时的车流速度;(2)、当车流量(辆/小时)是单位时间内通过桥上某观测点的车辆数,即:车流量=车流速度×车流密度.当 时,求高架桥上车流量 的最大值.23. 矩形 中, , , 是边 上的点,且 , 是直线 上的一点,连接 、 、 .
(1)、轻症患者的人数是多少?(2)、所有患者的平均治疗费用是多少万元?(3)、由于部分轻症患者康复出院,为减少病房拥挤,拟对某病房中的 、 、 、 、 五位患者任选两位转入另一病房,请用树状图法或列表法求出恰好选中 、 两位患者的概率.22. 为了解交通拥堵情况,经统计分析,某高架桥上的车流速度 (千米小时)是车流密度 (辆千米)的函数,当桥上的车流密度达到220辆/千米时,造成堵塞,此时车流速度为0千米/小时;当车流密度为20辆/千米时,车流速度为80千米/小时,研究表明:当 时,车流速度 是车流密度 的一次函数.(1)、某高架桥上车流密度为100辆/千米时的车流速度;(2)、当车流量(辆/小时)是单位时间内通过桥上某观测点的车辆数,即:车流量=车流速度×车流密度.当 时,求高架桥上车流量 的最大值.23. 矩形 中, , , 是边 上的点,且 , 是直线 上的一点,连接 、 、 .

 (1)、如图1,若 ,求 的长;(2)、如图2,将 沿 折叠至点 落在 上, 与 交于点 ,求 的长;(3)、如图3,若 ,求 的大小.
(1)、如图1,若 ,求 的长;(2)、如图2,将 沿 折叠至点 落在 上, 与 交于点 ,求 的长;(3)、如图3,若 ,求 的大小.