安徽省合肥市长丰县2021年中考数学一模试卷
试卷更新日期:2021-06-22 类型:中考模拟
一、单选题
-
1. -2021的绝对值等于( )A、2021 B、-2021 C、 D、2. 下列各式,计算正确的是( )A、 B、 C、 D、3. 由功夫明星吴京自导自演的军事体裁动作大片《战狼2》于2017年7月27日起在全国各大影院同期放映,激发了广大华人强烈的爱国热情,国人纷纷踊跃购票观影,票房统计达到人民币约56.94亿元.其中56.94亿用科学记数法表示为( )A、 B、 C、 D、4. 如果 ,那么 , 的值分别是( )A、 , B、 , C、 , D、 ,5. 如图,小亮用6个相同的小正方体搭成一个立体图形,研究几何体的三视图的变化情况,若由图①变到图②,其三视图中不改变的是( )
 A、主视图 B、主视图和左视图 C、主视图和俯视图 D、左视图和俯视图6. 一种商品原价100元,经过两次降价后的售价是60元,设平均每次降价的百分率为 ,那么所列方程正确的是( )A、 B、 C、 D、7. 下面四个图形中,∠1=∠2一定成立的是( )A、
A、主视图 B、主视图和左视图 C、主视图和俯视图 D、左视图和俯视图6. 一种商品原价100元,经过两次降价后的售价是60元,设平均每次降价的百分率为 ,那么所列方程正确的是( )A、 B、 C、 D、7. 下面四个图形中,∠1=∠2一定成立的是( )A、 B、
B、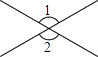 C、
C、 D、
D、 8. 如图,在平面直角坐标系中,函数 与 的图像交于点 ,则代数式 的值为( )
8. 如图,在平面直角坐标系中,函数 与 的图像交于点 ,则代数式 的值为( )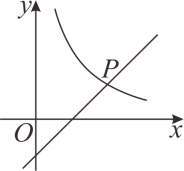 A、 B、 C、 D、9. 如图,在扇形 中, ,点 是 的中点,点 、 分别为半径 , 上的动点.若 ,则 周长的最小值为( )
A、 B、 C、 D、9. 如图,在扇形 中, ,点 是 的中点,点 、 分别为半径 , 上的动点.若 ,则 周长的最小值为( )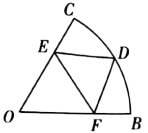 A、2 B、 C、4 D、10. 如图,等腰 中, ,AC与正方形DEFG的的边长DE在同一直线上, ,开始时点C与点D重合,让 沿直线DE向右平移,到点A与点E重合时停止.设CD的长为x , 与正方形DEFG重合部分的面积为y , 则能表示y与x之间关系的图象大致是( ).
A、2 B、 C、4 D、10. 如图,等腰 中, ,AC与正方形DEFG的的边长DE在同一直线上, ,开始时点C与点D重合,让 沿直线DE向右平移,到点A与点E重合时停止.设CD的长为x , 与正方形DEFG重合部分的面积为y , 则能表示y与x之间关系的图象大致是( ). A、
A、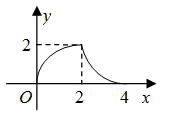 B、
B、 C、
C、 D、
D、
二、填空题
-
11. 不等式 的最小整数解是 .12. 分解因式: .13. 直角三角形斜边上的中线等于斜边的一半逆命题14. 定义 ,比如, , .若实数 满足 ,并且这个关于 的方程有两个不相等的实数解,则 的取值范围是 .
三、解答题
-
15. .16. 我国古代算术名著《算法统宗》中有这样一道题,原文如下:
一百馒头一百僧,大僧三个更无争,小僧三人分一个,大小和尚各几丁?大意为:有100个和尚分100个馒头,正好分完.如果大和尚一人分3个,小和尚3人分一个,试问大、小和尚各有几人?
请列方程(或方程组)解答上述问题.
17. 如图, 三个顶点的坐标分别为 , , .
( 1 )以点 为位似中心,在第一象限内将 放大为原来的2倍,得到 ,请在网格中画出 ,并写出点 的坐标;
( 2 )将 向左平移5个单位,再向上平移1个单位,得到 ,请在网格中画出 ;
( 3 )若 的内心为 ,请直接写出 的内心 的坐标(用含 或 的代数式表示).
18. 观察下列等式:① ;② ;③ ;……
(1)、请按以上规律写出第④个等式:;(2)、猜想并写出第 个等式:;(3)、请证明猜想的正确性.19. 如图是某校在教学楼前新建的升旗杆 ,小明和小亮想利用刚学的三角函数知识来测算旗杆 的高度.小明在一楼底部 处测得旗杆顶部的仰角为 ,小亮在三楼 处测得旗杆顶部的仰角为 ,已知旗杆底部与教学楼一楼底部在同一水平线上,每层楼的高度为 ,求旗杆 的高度.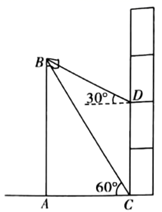 20. 已知:如图,直线 经过两个等腰直角 和 的顶点 , ,连接 , ,且 于点 , 与直线 交于点 .求证:点 是 的中点.
20. 已知:如图,直线 经过两个等腰直角 和 的顶点 , ,连接 , ,且 于点 , 与直线 交于点 .求证:点 是 的中点.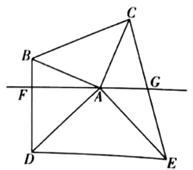 21. 学校为了了解七年级学生的跳绳成绩,韦老师随机调查了该年级开学体育模拟考试中部分同学的跳绳成绩,并绘制成了如图所示的条形统计图和扇形统计图.请你根据图中提供的信息完成下各题:
21. 学校为了了解七年级学生的跳绳成绩,韦老师随机调查了该年级开学体育模拟考试中部分同学的跳绳成绩,并绘制成了如图所示的条形统计图和扇形统计图.请你根据图中提供的信息完成下各题: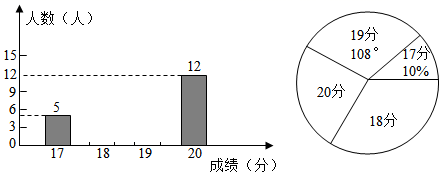 (1)、被调查同学跳绳成绩的中位数是 , 并补全条形统计图;(2)、如果该校七年级共有学生2025人,估计跳绳成绩能得18分的学生约有人;(3)、在成绩为20分的同学中有三人(两男一女)的跳绳水平很高,现准备从他们中随机选出两位同学给全年级同学作示范,请用画树状图或列表法求刚好抽到两位男生的概率.22. 对于二次函数 和一次函数 ,我们把 称为这两个函数的“再生二次函数”,其中t是不为零的实数,其图象记作抛物线E.现有点A(1,0)和抛物线E上的点B(2,n),请完成下列任务:
(1)、被调查同学跳绳成绩的中位数是 , 并补全条形统计图;(2)、如果该校七年级共有学生2025人,估计跳绳成绩能得18分的学生约有人;(3)、在成绩为20分的同学中有三人(两男一女)的跳绳水平很高,现准备从他们中随机选出两位同学给全年级同学作示范,请用画树状图或列表法求刚好抽到两位男生的概率.22. 对于二次函数 和一次函数 ,我们把 称为这两个函数的“再生二次函数”,其中t是不为零的实数,其图象记作抛物线E.现有点A(1,0)和抛物线E上的点B(2,n),请完成下列任务:(尝试)
(1)、当t=2时,抛物线 的顶点坐标为(2)、判断点A是否在抛物线E上;(3)、求n的值.(发现)通过(2)和(3)的演算可知,对于t取任何不为零的实数,抛物线E总过定点,定点的坐标 ▲ .
(应用)二次函数 是二次函数 和一次函数 的一个“再生二次函数”吗?如果是,求出t的值;如果不是,说明理由.
23. (问题提出)已知一个三角形的三条边长,怎样求出其内角平分线的长度?(问题转化)
(1)、已知:如图1, 中, 是内角平分线.求证: ;(2)、已知:如图2, 内接于 ,延长 的内角平分线 交 于点 .求证: ;(3)、(问题解决)已知:如图3, 中, , , , 是 的内角平分线.求 的长;
(4)、已知:如图3, 中, , , , 是 的内角平分线.请直接写出求 的计算公式: .