初中数学苏科版七年级上册第六章 平面图形的认识（一） 同步测试卷
试卷更新日期：2021-06-22 类型：单元试卷
一、单选题
-
1. 下列说法正确的是（ ）A、具有公共顶点的两个角是对顶角 B、 两点之间的距离就是线段 C、两点之间，线段最短 D、不相交的两条直线叫做平行线2. 下列说法不正确的是（ ）A、对顶角相等 B、两点确定一条直线 C、一个角的补角一定大于这个角 D、垂线段最短3. 下列说法错误的是（ ）A、平面内过一点有且只有一条直线与已知直线平行 B、平面内过一点有且只有一条直线与已知直线垂直 C、两点之间的所有连线中，线段最短 D、对顶角相等4. 如图，∠ACB＝90°，CD⊥AB，D为垂足.下列判断错误的是（ ）
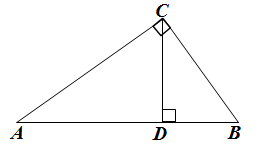A、∠A=∠B B、∠A=∠BCD C、AC>AD D、BC>CD5. 如图，已知点A是射线BE上一点，过A作AC⊥BF，垂足为C，CD⊥BE，垂足为D.给出下列结论：①∠1是∠ACD的余角；②图中互余的角共有3对；③∠1的补角只有∠DCF；④与∠ADC互补的角共有3个.其中正确结论有（ ）
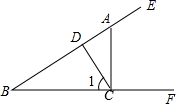A、① B、①②③ C、①④ D、②③④6. 下列时刻中，时针与分针所成的角（小于平角）最大的是（ ）A、9：00 B、3：30 C、6：40 D、5：45二、填空题
-
7. 已知直线 与直线 相交于点 ， ，垂足为 ．若 ，则 的度数为 ． (单位用度表示)
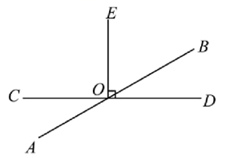8. 如图，直线AB与CD相交于点O ， ，若 ，则 =°．
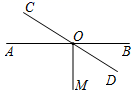9. G101是一班从北京南站开往上海虹桥的下行（单向）高速列车，停靠如图所示的11个站点，则该趟列车共有个乘车区间（指旅客乘车地与目的地之间的区间）．
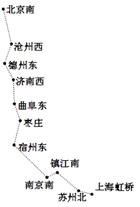10. 数轴上有点A和点B，点A到原点的距离为m，点B到原点的距离为n，且点B在点A的左边，若m＜n，则点A与点B的距离等于.11. 数轴上A点表示的数为－2，则A点相距3个单位长度的点表示的数是12. 数轴上表示有理数﹣5.5与3.5两点的距离是.13. 在平面直角坐标系中，若点M（﹣2，3）与点N（x，3）之间的距离是5，则x的值是.14. 已知 与 互为余角， ，则 ．15. 如图，已知 .若 ，则 ．
16. 58°36′=°．17. 如图，A在B的方向．
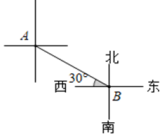18. 如图，点B在点A北偏东40°方向，点C在点B北偏西50° 方向， BC=10m，则点 C到直线 AB的距离为 m.
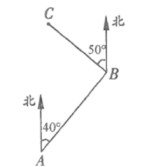19. 下列三个日常现象：①用两根钉子就可以把一根木条固定在墙上；②把弯曲的公路改直，就能够缩短路程；③体育课上，老师测量某名同学的跳远成绩．其中，可以用“两点之间线段最短”来解释的是 .(填序号)
20. 若∠α＝68 ，则∠α的余角为 ．21. 已知∠α=25°15′，∠β=25.15°，则∠α∠β（填“＞”，“＜”或“＝”）．22. 若∠α＝40° 15′，则∠α的余角等于°．23. 已知 ，则 的余角的度数是.24. 下午3点30分时，钟面上时针与分针所成的角等于°.25. 已知∠A＝40°，则∠A的余角等于.
26. 北京时间上午5点整，时针与分针所成的角的度数是.27. 已知∠α＝28°，则∠α的补角为°．三、计算题
-
28.(1)、(2)、(3)、29. 计算：
（1）﹣22÷﹣（﹣）×（﹣3）2
（2）16°51′+38°27′×3﹣35°29′．
四、作图题
-
30. 画图，探究：
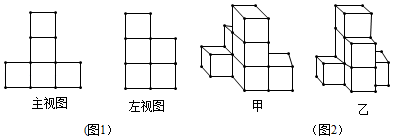(1)、一个正方体组合图形的主视图、左视图（如图1）所示．①这个几何体可能是（图2）甲、乙中的；
②这个几何体最多可由个小正方体构成，请在图3中画出符合最多情况的一个俯视图．
(2)、如图，已知一平面内的四个点A、B、C、D，根据要求用直尺画图．①画线段AB，射线AD；
②找一点M，使M点即在射线AD上，又在直线BC上；
③找一点N，使N到A、B、C、D四个点的距离和最短．
31. 如图，已知直线l和直线外三点A，B，C，按下列要求画图：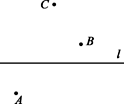
①画射线CB交直线l于点F；
②连接BA；
③在直线l上确定点E，使得AE+CE最小.
五、综合题
-
32. 有一科技小组进行了机器人行走性能试验，在试验场地有A、B、C三点顺次在同一笔直的赛道上，A、B两点之间的距离是90米，甲、乙两机器人分别从A、B两点同时同向出发到终点C，乙机器人始终以50米分的速度行走，乙行走9分钟到达C点.设两机器人出发时间为t（分钟），当t＝3分钟时，甲追上乙.
请解答下面问题：
(1)、B、C两点之间的距离是米.(2)、求甲机器人前3分钟的速度为多少米/分？(3)、若前4分钟甲机器人的速度保持不变，在4≤t≤6分钟时，甲的速度变为与乙相同，求两机器人前6分钟内出发多长时间相距28米？(4)、若6分钟后甲机器人的速度又恢复为原来出发时的速度，直接写出当t＞6时，甲、乙两机器人之间的距离S.（用含t的代数式表示）.33. 阅读下面材料：如图，点A、B在数轴上分别表示有理数a、b，则A、B两点之间的距离可以表示为|a−b|.
根据阅读材料与你的理解回答下列问题：
(1)、数轴上表示3与−2的两点之间的距离是.(2)、数轴上有理数x与有理数7所对应两点之间的距离用绝对值符号可以表示为.(3)、代数式|x+8|可以表示数轴上有理数x与有理数 所对应的两点之间的距离；若|x+8|=5，则x=.(4)、求代数式|x+2018|+|x+504|+|x−2017|的最小值.34. 已知数轴上有A、B、C三点，分别代表-24，-10，10，两只电子蚂蚁甲、乙分别从A、C两点同时相向而行，甲的速度为4个单位/秒，乙的速度为6个单位/秒.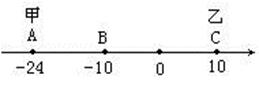
(1)、甲、乙多少秒后相遇？(2)、甲出发多少秒后，甲到A、B、C三点的距离和为40个单位？(3)、当甲到A、B、C三点的距离和为40个单位时，甲调头返回，当甲、乙在数轴上再次相遇时，相遇点表示的数是.35. 如图，已知数轴上有A、B、C三个点，它们表示的数分别是18，8，﹣10．
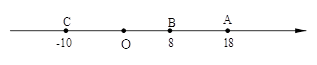(1)、填空：AB= ， BC=；(2)、若点A以每秒1个单位长度的速度向右运动，同时，点B和点C分别以每秒2个单位长度和5个单位长度的速度向左运动．试探索：BC﹣AB的值是否随着时间t的变化而改变？请说明理由．(3)、现有动点P、Q都从A点出发，点P以每秒1个单位长度的速度向终点C移动；当点P移动到B点时，点Q才从A点出发，并以每秒3个单位长度的速度向左移动，且当点P到达C点时，点Q就停止移动．设点P移动的时间为t秒，试用含t的代数式表示P、Q两点间的距离．36. 阅读下面材料：若点A、B在数轴上分别表示数a，b，则A、B两点之间的距离表示为|AB|
(1)、数轴上表示2和5两点之间的距离是 ， 数轴上表示-3和4两点之间的距离是 ．(2)、若数轴上点B表示的数是-1，且|AB| = 3，则a= ．(3)、在数轴上有三个点A， B， C若点A表示的数是-1，点B表示的数是3，且|AB| + |AC| = 6 ，求点C表示的数．37. 已知在纸面上有一数轴 如图 ，折叠纸面：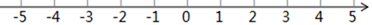
(1)、若1表示的点与-1表示的点重合，则 表示的点与数表示的点重合；(2)、若-1表示的点与5表示的点重合，回答以下问题：①6表示的点与数表示的点重合；
②若数轴上A、B两点之间的距离为 在B的左侧 ，且A、B两点经折叠后重合，求A、B两点表示的数是多少？
38. 如图，点P、Q在数轴上表示的数分别是-8、4，点P以每秒2个单位的速度运动，点Q以每秒1个单位的速度运动.设点P、Q同时出发，运动时间为t秒.
(1)、若点P、Q同时向右运动2秒，则点P表示的数为 ， 点P、Q之间的距离是个单位；(2)、经过秒后，点P、Q重合；(3)、试探究：经过多少秒后，点P、Q两点间的距离为14个单位.39. 已知A、B两点在数轴上表示的数分别为a，b.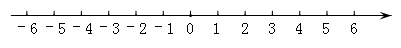
(1)、对照数轴填写下表：a
6
－6
－6
－6
b
4
0
4
6
A、B两点的距离
(2)、若A、B两点间的距离记为d，则d=（用含a、b的式子表示）；(3)、在数轴上到6和－6的距离之和为12的整数点共有个；(4)、若数轴上点C表示的数为x，当x在和之间取值时， 的值最小，最小值是 ， 此时x的整数值为.40. 阅读下列内容：数轴上表示数a的点与原点的距离叫做数a的绝对值，记作|a|.数轴上表示数a的点与表示数b的点的距离记作|a﹣b|，如|3﹣5|表示数轴上表示数3的点与表示数5的点的距离，|3+5|＝|3﹣（﹣5）|表示数轴上表示数3的点与表示数﹣5的点的距离，|a﹣3|表示数轴上表示数a的点与表示数3的点的距离.
根据以上材料回答下列问题：（将结果直接填写在答题卡相应位置，不写过程）
(1)、若|x﹣1|=|x+1|，则x= ， 若|x﹣2|＝|x+1|，则x=；(2)、若|x﹣2|+|x+1|=3，则x的取值范围是；(3)、若|x﹣2|+|x+1|=5，则x的值是；(4)、若|x﹣2|﹣|x+1|=3，则x能取到的最大值是.