安徽省合肥市瑶海区2021年中考数学三模试卷
试卷更新日期:2021-06-22 类型:中考模拟
一、单选题
-
1. 2的相反数是( )A、 B、 C、2 D、-22. 第七次全国人口普查结果显示我国总人口为14.1178亿人,其中14.1178亿用科学记数法表示为( )A、 B、 C、 D、3. 计算 的结果是( )A、 B、 C、 D、4. 如图所示的几何体的主视图、左视图、俯视图中有两个视图是相同的,则相同的视图是( )
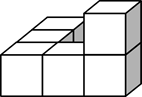 A、
A、 B、
B、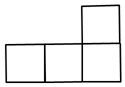 C、
C、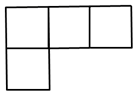 D、
D、 5. 下列四个选项中为多项式 的因式是( )A、 B、 C、 D、6. 下表是某校男子排球队队员的年龄分布,则这些队员年龄的中位数(岁)是( )
5. 下列四个选项中为多项式 的因式是( )A、 B、 C、 D、6. 下表是某校男子排球队队员的年龄分布,则这些队员年龄的中位数(岁)是( )年龄/岁
13
14
15
16
人数
1
5
4
2
A、14 B、14.5 C、15 D、167. 某旅游景点三月份共接待游客25万人次,五月份共接待游客64万人次,设每月的平均增长率为 ,则可列方程为( )A、 B、 C、 D、8. 如图,在正方形ABCD中,AB=2,延长AB至点E,使得BE=1,EF⊥AE,EF=AE.分别连接AF,CF,M为CF的中点,则AM的长为( )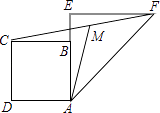 A、2 B、3 C、 D、9. 如图①,在矩形 中, 、 交于点 ,点 在边 上运动, 于点 , 于点 ,设 , .且 与 满足一次函数关系,其图象如图②所示,其中 ,以下判断中,错误的是( )
A、2 B、3 C、 D、9. 如图①,在矩形 中, 、 交于点 ,点 在边 上运动, 于点 , 于点 ,设 , .且 与 满足一次函数关系,其图象如图②所示,其中 ,以下判断中,错误的是( )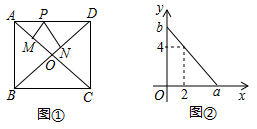 A、 中斜边 上的高为6 B、无论点 在 上何处, 与 的和始终保持不变 C、当 时, 垂直平分 D、若 ,则矩形 的面积为6010. 甲、乙两辆汽车沿同路线从 地前住 地, 、 两地间的距离为240千米,甲车以40千米时的速度与速行驶,行驶3小时后出现故障,停车维修1小时,修好后以80千米时的速度继续行驶;乙车在甲车出发2小时后以80千米时的速度匀速前往 地,甲、乙两车到达 地后均作停留,下列选项中,能符合题意反映两车与 地之同的距离 (千米)与甲车出发的时间 (小时)的函数图象是( )A、
A、 中斜边 上的高为6 B、无论点 在 上何处, 与 的和始终保持不变 C、当 时, 垂直平分 D、若 ,则矩形 的面积为6010. 甲、乙两辆汽车沿同路线从 地前住 地, 、 两地间的距离为240千米,甲车以40千米时的速度与速行驶,行驶3小时后出现故障,停车维修1小时,修好后以80千米时的速度继续行驶;乙车在甲车出发2小时后以80千米时的速度匀速前往 地,甲、乙两车到达 地后均作停留,下列选项中,能符合题意反映两车与 地之同的距离 (千米)与甲车出发的时间 (小时)的函数图象是( )A、 B、
B、 C、
C、 D、
D、
二、填空题
-
11. 计算: =
12. “正方形对角线互相垂直平分”的逆命题是(填“真命题”或“假命题”).13. 如图, 的直角顶点 ,另一顶点 及斜边 的中点 都在 上, , ,则 的半径为 . 14. 如图, 和 都是等腰直角三角形, ,且点 、 、 在同一条直线上,连接 .
14. 如图, 和 都是等腰直角三角形, ,且点 、 、 在同一条直线上,连接 . (1)、 的度数为 .(2)、若 、 分别是 、 的中点,连接 , , ,则 的值为 .
(1)、 的度数为 .(2)、若 、 分别是 、 的中点,连接 , , ,则 的值为 .三、解答题
-
15. 计算: ,其中 .16. 观察下列等式:
第1个等式: ; 第2个等式: ;
第3个等式: ; 第4个等式: ;
第5个等式: ;
按照以
上规律,解决下列问题:
(1)、写出第6个等式: .(2)、写出你猜想的第 个等式: ▲ . (用含 的等式表示),并证明.17. 如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点四边形 (顶点是网格线的交点)和格点 .
( 1 )把四边形 平移,使得顶点 与 重合,画出平移后得到的四边形 ;
( 2 )把四边形 绕 点顺时针旋转90°,画出旋转后得到的四边形 .
18. 安徽滁州琅琊山会峰阁更名为琅琊阁,如图①是悬挂着巨大匾额的琅琊阁,如图②,线段 是悬挂在墙壁 上的匾额的截面示意图,已知 米, ,从水平地面点 处看点 ,仰角 ,从点 处看点 ,仰角 .且 米,求匾额悬挂的高度 的长.(结果精确到0.1米,参考数据: , , ). 19. 为了减少雾霾,美化环境,小王上班的交通方式由驾车改为骑自行车,小王家距单位的路程是15千米,在相同的路线上,小王驾车的速度是骑自行车速度的4倍,小王每天骑自行车上班比驾车上班要早出发45分钟,才能按原时间到达单位,求小王骑自行车的速度.20. 如图,已知 是 的直径, 于点 ,连接 ,弦 ,直线 交直线 于点 .
19. 为了减少雾霾,美化环境,小王上班的交通方式由驾车改为骑自行车,小王家距单位的路程是15千米,在相同的路线上,小王驾车的速度是骑自行车速度的4倍,小王每天骑自行车上班比驾车上班要早出发45分钟,才能按原时间到达单位,求小王骑自行车的速度.20. 如图,已知 是 的直径, 于点 ,连接 ,弦 ,直线 交直线 于点 . (1)、求证:直线 是 的切线:(2)、若 , , ,求 的长.21. 某校在倡导“光盘行动”活动中,在食堂随机观察50名学生午餐剩余情况并据此打分(以百分制呈现,分数都大于49.5且为整数),统计后绘制了频数分布表和频数分布直方图,部分信息如下:
(1)、求证:直线 是 的切线:(2)、若 , , ,求 的长.21. 某校在倡导“光盘行动”活动中,在食堂随机观察50名学生午餐剩余情况并据此打分(以百分制呈现,分数都大于49.5且为整数),统计后绘制了频数分布表和频数分布直方图,部分信息如下:频数分布表
分组
分数
频数
第一组
16
第二组
20
第三组
第四组
第五组
2
合计
50
 (1)、补全频数分布表和频数分布直方图;(2)、据此估计全校2000名学生午餐剩余情况高于80分(含80分)的人数为 , 如果将本次统计结果绘制成扇形统计图,那么午餐剩余情况高于80分(含80分)的人数所占扇形的圆心角的度数为 .(3)、若从以上第四组和第五组的学生中随机挑选2名学生为学校午餐“光盘行动”监督员.求挑选的2名学生恰好都在第五组的概率.22. 春节期间商家销售某种纪念品,进价为12元/只,售价为20元/只,为了促销,该商家决定凡是一次购买10只以上的,每多买一只,售价就降低0.10元[例如:某人买20只这种纪念品,于是每只降价 元,就可以按19元/只的价格购买],但是最低价为16元/只,(1)、求顾客一次至少购买多少只,才能以最低价购买?(2)、求出当一次购买 只时,总利润 (元)与购买量 (只)之间的函数关系式;(3)、有一天,一位顾客一次购买了46只,另一位顾客一次购买了50只,商家发现卖了50只反而比卖46只赚的钱少,为了使每次卖的数量越多赚的钱也越多,在其他促销条件不变的情况下,最低价16元/只至少要提高到多少?为什么?23. 如图1,四边形 是正方形, ,连接 , 是等腰直角三角形, , 交 于点 .
(1)、补全频数分布表和频数分布直方图;(2)、据此估计全校2000名学生午餐剩余情况高于80分(含80分)的人数为 , 如果将本次统计结果绘制成扇形统计图,那么午餐剩余情况高于80分(含80分)的人数所占扇形的圆心角的度数为 .(3)、若从以上第四组和第五组的学生中随机挑选2名学生为学校午餐“光盘行动”监督员.求挑选的2名学生恰好都在第五组的概率.22. 春节期间商家销售某种纪念品,进价为12元/只,售价为20元/只,为了促销,该商家决定凡是一次购买10只以上的,每多买一只,售价就降低0.10元[例如:某人买20只这种纪念品,于是每只降价 元,就可以按19元/只的价格购买],但是最低价为16元/只,(1)、求顾客一次至少购买多少只,才能以最低价购买?(2)、求出当一次购买 只时,总利润 (元)与购买量 (只)之间的函数关系式;(3)、有一天,一位顾客一次购买了46只,另一位顾客一次购买了50只,商家发现卖了50只反而比卖46只赚的钱少,为了使每次卖的数量越多赚的钱也越多,在其他促销条件不变的情况下,最低价16元/只至少要提高到多少?为什么?23. 如图1,四边形 是正方形, ,连接 , 是等腰直角三角形, , 交 于点 . (1)、若 交 边于点 ,连接 ,求证: .(2)、连接 ,求证: 是等腰直角三角形.(3)、如图2,若 交直线 于点 , 交 于点 ,交 的延长线于点 ,连接 ,若 是 的中点,求 的长.
(1)、若 交 边于点 ,连接 ,求证: .(2)、连接 ,求证: 是等腰直角三角形.(3)、如图2,若 交直线 于点 , 交 于点 ,交 的延长线于点 ,连接 ,若 是 的中点,求 的长.