安徽省合肥市第四十五中2021年中考数学四模试卷
试卷更新日期:2021-06-22 类型:中考模拟
一、单选题
-
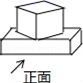
1. 有理数 的绝对值为( )A、2021 B、 C、 D、2. 下列运算正确的是( )A、 B、 C、 D、3. 纳米是一种长度单位,1纳米 米,若用科学记数法表示110纳米,则正确的结果是( )A、 米 B、 米 C、 米 D、 米4. 若将两个立方体图形按如图所示的方式放置,则所构成的几何体的左视图可能是( ).
 A、
A、 B、
B、 C、
C、 D、
D、 5. 某数学兴趣小组为了了解本班学生一周课外阅读的时间,随机调查5名学生,并将所得数据整理如表表中有一个数字被污染而模糊不清,但曾计算得该组数据的平均数为6,则这组数据的方差和中位数分别为( )
5. 某数学兴趣小组为了了解本班学生一周课外阅读的时间,随机调查5名学生,并将所得数据整理如表表中有一个数字被污染而模糊不清,但曾计算得该组数据的平均数为6,则这组数据的方差和中位数分别为( )学生编号
1
2
3
4
5
一周课外阅读时间(小时)
7
5
4

8
A、2,6 B、1.5,4 C、2,4 D、6,66. 如图,将一副三角板和一张对边平行的纸条按下列方式摆放,两个三角板的一直角边重合,含 角的直角三角板的斜边与纸条一边重合,含 角的三角板的一个顶点在纸条的另一边上,则 的度数是( ) A、 B、 C、 D、7. 某药店在防治新冠病毒期间,市场上抗病毒用品紧缺的情况下,将某药品提价100%,物价部门查处后,限定其提价幅度只能是原价的14%,则该药品现在降价的幅度是( )A、43% B、45% C、57% D、55%8. 根据表格中的信息,估计一元二次方程 ( 、 、 为常数, )的一个解 的范围为( )
A、 B、 C、 D、7. 某药店在防治新冠病毒期间,市场上抗病毒用品紧缺的情况下,将某药品提价100%,物价部门查处后,限定其提价幅度只能是原价的14%,则该药品现在降价的幅度是( )A、43% B、45% C、57% D、55%8. 根据表格中的信息,估计一元二次方程 ( 、 、 为常数, )的一个解 的范围为( )x
0
1
2
3
4
ax2+bx+c
-14.5
-11.5
-6.5
0.5
9.5
A、 B、 C、 D、9. 如图, 中, , ,点 在 的延长线上,且 连接 并延长,过 作 于点 ,若 ,则 的面积为( )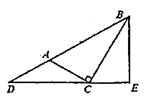 A、1 B、2 C、 D、10. 如图1,在等边三角形 和矩形 中, ,点 , , 都在直线 上,且 于点 , 于点 ,且 , , 三点共线,将矩形 以每秒1个单位长度的速度从左向右匀速运动,直至矩形 和 :无重叠部分;设矩形 运动的时间为 秒,矩形 和 重叠部分的面积为 ;图2为 随 的变化而变化的函数图象,则函数图象中点 的纵坐标是( )
A、1 B、2 C、 D、10. 如图1,在等边三角形 和矩形 中, ,点 , , 都在直线 上,且 于点 , 于点 ,且 , , 三点共线,将矩形 以每秒1个单位长度的速度从左向右匀速运动,直至矩形 和 :无重叠部分;设矩形 运动的时间为 秒,矩形 和 重叠部分的面积为 ;图2为 随 的变化而变化的函数图象,则函数图象中点 的纵坐标是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 的平方根是 .12. 如图,点 、 、 在圆 上,点 是 延长线上一点,若 ,则 的度数为 .
 13. 如图,一次函数 的图象与y轴交于点 ,与反比例函数 的图象交于点 .以 为对角线作矩形 ,使顶点 , 落在 轴上(点 在点 的右边), 与 交于点 .则 .
13. 如图,一次函数 的图象与y轴交于点 ,与反比例函数 的图象交于点 .以 为对角线作矩形 ,使顶点 , 落在 轴上(点 在点 的右边), 与 交于点 .则 . 14. 如图所示,已知直线 , 、 之间的距离为1, 、 点分别在直线 、 上, 、 分别为直线 、直线 上的动点,使 ,且 .
14. 如图所示,已知直线 , 、 之间的距离为1, 、 点分别在直线 、 上, 、 分别为直线 、直线 上的动点,使 ,且 . (1)、 的值为.(2)、 在运动的过程中, 的最小值为 .
(1)、 的值为.(2)、 在运动的过程中, 的最小值为 .三、解答题
-
15. 解不等式组: ,并把它的解集在数轴上表示出来.16. 由于疫情防控的需要,学校开学第一周给某班配备了一定数量的口罩,若每个学生发5个,则多40个口罩,若每个学生发6个,则少12个口罩,请问该班有多少名学生?学校给该班准备了多少个口罩?17. 如图,在平面直角坐标系中, 中 点的坐标为 , 点的坐标为 .

( 1 )将 绕点 顺时针旋转 得到 ,请你画出旋转后的图形;
( 2 )请用无刻度直尺作 的角平分线 ,并直接写出点 的坐标.
18. 桌面上的某创意可折叠台灯的平面示意图如图1所示,将其抽象成图2,量得 , ﹔灯杆 的长为30cm,灯管 的长为20cm,底座 的厚度为3cm,不考虑其他因素,求台灯的高(点 到桌面的距离,结果保留根号). 19. 观察下列等式:
19. 观察下列等式:① ②
② ④
……
(1)、请按以上规律写出第⑤个等式;(2)、猜想并写出第n个等式 ▲ ;并证明猜想的符合题意性.20. 某校数学社团对该校学生进行“舌尖上的合肥——我最喜爱的合肥小吃”随机调查,每人只能从中“ .锅贴、 .鸡蛋灌饼、 .小笼包、 .赤豆糊”中选择一个本人最喜欢的小吃.将调查问卷整理后绘制了如下两幅不完整的统计图.请结合统计图中的信息,解决下列问题:
 (1)、小笼包所在扇形的圆心角的度数为 ,将条形统计图补充完整;(2)、该校共有1200名同学,估计最喜欢赤豆糊的同学有名;(3)、甲、乙两个同学从这四种小吃:“ .锅贴、 .鸡蛋灌饼、 小笼包、 .赤豆糊”中随机地选一项去品尝,请你利用树状图或表格,求出两位同学选到 、 小吃的概率.21. 直线 交 于点 、 两点, 是 的直径, 平分 交 于 ,过 作 于 ,若 , .
(1)、小笼包所在扇形的圆心角的度数为 ,将条形统计图补充完整;(2)、该校共有1200名同学,估计最喜欢赤豆糊的同学有名;(3)、甲、乙两个同学从这四种小吃:“ .锅贴、 .鸡蛋灌饼、 小笼包、 .赤豆糊”中随机地选一项去品尝,请你利用树状图或表格,求出两位同学选到 、 小吃的概率.21. 直线 交 于点 、 两点, 是 的直径, 平分 交 于 ,过 作 于 ,若 , .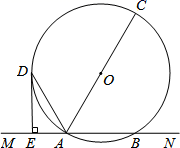 (1)、 的半径;(2)、圆心 点到 距离.
(1)、 的半径;(2)、圆心 点到 距离.