四川省眉山市2020-2021学年高三上学期第一次诊断性考试理科数学试题
试卷更新日期:2021-06-22 类型:高考模拟
一、单选题
-
1. 已知集合 , ,则 ( )A、 B、 C、 D、 或2. 若 ,则复数 在复平面内所对应的点位于( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 若 ,则 ( )A、 B、 C、 D、4. 已知直线 是圆 在点 处的切线﹐则直线 的方程为( )A、 B、 C、 D、5. 如图,在 中, 为线段 上异于 , 的任意一点, 为 的中点,若 ,则 ( )
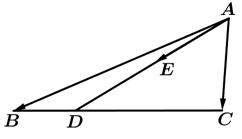 A、 B、 C、 D、6. 居民消费价格指数 ,简称 )是根据与居民生活有关的产品及劳务价格统计出来的物价变动指标,它是进行经济分析和决策、价格总水平监测和调控及国民经济核算的重要指标.根据下面给出的我国2019年9月-2020年9月的居民消费价格指数的同比(将上一年同月作为基期进行对比的价格指数)增长和环比(将上月作为基期进行对比的价格指数)增长情况的折线图,以下结论正确的是( )
A、 B、 C、 D、6. 居民消费价格指数 ,简称 )是根据与居民生活有关的产品及劳务价格统计出来的物价变动指标,它是进行经济分析和决策、价格总水平监测和调控及国民经济核算的重要指标.根据下面给出的我国2019年9月-2020年9月的居民消费价格指数的同比(将上一年同月作为基期进行对比的价格指数)增长和环比(将上月作为基期进行对比的价格指数)增长情况的折线图,以下结论正确的是( )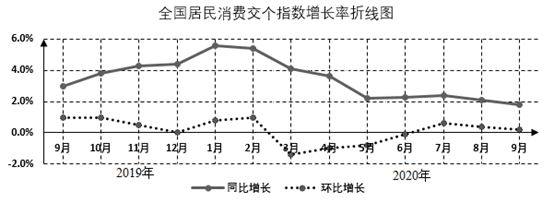 A、2020年1月到9月的居民消费价格指数在逐月增大 B、2019年9月到2020年9月的居民消费价格指数在逐月减小 C、2020年1月到9月的居民消费价格指数分别低于2019年同期水平 D、2020年7月过后,居民消费价格指数的涨幅有回落趋势7. 2020年北京冬季奥运会组委会招聘了5名志愿者,分别参与冰壶、冰球、花样滑冰、自由式滑雪、越野滑雪五项比赛项目的前期准备工作.若每个人只能担任其中一项工作,且志愿者甲不能在越野滑雪项目,则不同的派遣方法种数共有( )A、120 B、96 C、48 D、248. 函数 的大致图象是( )A、
A、2020年1月到9月的居民消费价格指数在逐月增大 B、2019年9月到2020年9月的居民消费价格指数在逐月减小 C、2020年1月到9月的居民消费价格指数分别低于2019年同期水平 D、2020年7月过后,居民消费价格指数的涨幅有回落趋势7. 2020年北京冬季奥运会组委会招聘了5名志愿者,分别参与冰壶、冰球、花样滑冰、自由式滑雪、越野滑雪五项比赛项目的前期准备工作.若每个人只能担任其中一项工作,且志愿者甲不能在越野滑雪项目,则不同的派遣方法种数共有( )A、120 B、96 C、48 D、248. 函数 的大致图象是( )A、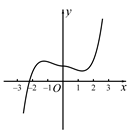 B、
B、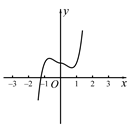 C、
C、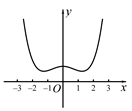 D、
D、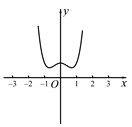 9. 已知双曲线 的离心率为 ,则双曲线 的一个焦点 到它的一条渐近线的距离为( )A、 B、 C、 D、210. 将函数 的图象向右平移 个单位长度后得到函数 的图象,且 的图象的一条对称轴是直线 ,则 的最小值为( )A、 B、2 C、3 D、11. 定义在 上的偶函数 满足 ,则 ( )A、-3或4 B、-4或3 C、3 D、412. 如图,已知四棱锥 中,四边形 为正方形,平面 平面 为 上一点,且 平面 ,则三棱锥 体积最大值为( )
9. 已知双曲线 的离心率为 ,则双曲线 的一个焦点 到它的一条渐近线的距离为( )A、 B、 C、 D、210. 将函数 的图象向右平移 个单位长度后得到函数 的图象,且 的图象的一条对称轴是直线 ,则 的最小值为( )A、 B、2 C、3 D、11. 定义在 上的偶函数 满足 ,则 ( )A、-3或4 B、-4或3 C、3 D、412. 如图,已知四棱锥 中,四边形 为正方形,平面 平面 为 上一点,且 平面 ,则三棱锥 体积最大值为( )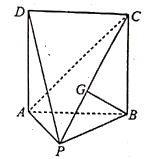 A、 B、 C、 D、2
A、 B、 C、 D、2二、填空题
-
13. 若 , 满足约束条件 ,则 的最大值为.14. 2021年第 届世界大学生夏季运动会将在成都举行.为营造“爱成都迎大运”全民运动和全民健身活动氛围,某社区组织甲、乙两队进行一场足球比赛,根据以往的经验知,甲队获胜的概率是 ,两队打平的概率是 ,则这次比赛乙队不输的概率是 .15. 给出下列命题:
①同时垂直于一条直线的两个平面互相平行﹔
②一条直线平行于一个平面,另一条直线与这个平面垂直,则这两条直线互相垂直;
③设 为平面,若 ,则 ;
④设 为平面,若 ,则 .
其中所有正确命题的序号为 .
16. 设函数 ,若存在唯一的整数 ,使得 ,则实数 的取值范围是 .三、解答题
-
17. 在数列 中, , .(1)、证明:数列 为等比数列,并求数列 的通项公式;(2)、若 ,求数列 的前 项和 .18. 在新冠肺炎疫情得到有效控制后,某公司迅速复工复产,为扩大销售额,提升产品品质,现随机选取了100名顾客到公司体验产品,并对体验的满意度进行评分(满分100分).体验结束后,该公司将评分制作成如图所示的直方图.
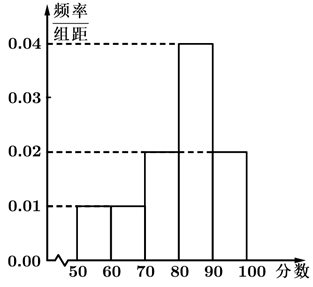 (1)、将评分低于80分的为“良”,80分及以上的为“优”.根据已知条件完成下面 列联表,能否在犯错误的概率不超过0.10的前提下认为体验评分为“优良”与性别有关.
(1)、将评分低于80分的为“良”,80分及以上的为“优”.根据已知条件完成下面 列联表,能否在犯错误的概率不超过0.10的前提下认为体验评分为“优良”与性别有关.良
优
合计
男
40
女
40
合计
(2)、为答谢顾客参与产品体验活动,在体验度评分为 和 的顾客中用分层抽样的方法选取了6名顾客发放优惠卡.若在这6名顾客中,随机选取4名再发放纪念品,记体验评分为 的顾客获得纪念品数为随机变量 ,求 的分布列和数学期望.附表及公式:
P(K2≥k0)
0.15
0.10
0.05
0.025
0.010
0.005
0.001
2.072
2.076
3.841
5.024
6.635
7.879
10.828
19. 如图,在平面五边形 中, , , .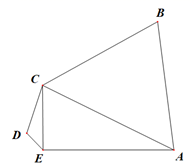 (1)、求AC的值;(2)、求 面积的最大值.20. 如图,在四棱锥 中, , 平面 , .
(1)、求AC的值;(2)、求 面积的最大值.20. 如图,在四棱锥 中, , 平面 , . (1)、证明: 是正三角形;(2)、若 平面 , ,求二面角 的余弦值.
(1)、证明: 是正三角形;(2)、若 平面 , ,求二面角 的余弦值.