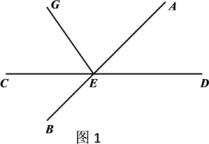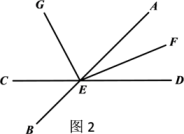初中数学苏科版七年级上册6.1-6.3 同步练习
试卷更新日期:2021-06-22 类型:同步测试
一、单选题
-
1. 在下列日常生活的操作中,能体现基本事实“两点之间,线段最短”的是( )A、用两颗钉子可以固定一根木条 B、把弯路改直可以缩短路程 C、用两根木桩拉一直线可把树栽成一排 D、沿桌子的一边看,可将桌子排整齐2. 如图是一副三角板摆成的图形,如果 ,那么 等于( )
 A、15° B、20° C、30° D、40°3. 如图,数轴的单位长度为1,如果点 表示的数为-2,那么点 表示的数是( ).
A、15° B、20° C、30° D、40°3. 如图,数轴的单位长度为1,如果点 表示的数为-2,那么点 表示的数是( ). A、-1 B、0 C、3 D、44. 如图, ,以 为一边作 ,则 的度数为( )
A、-1 B、0 C、3 D、44. 如图, ,以 为一边作 ,则 的度数为( )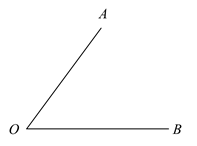 A、 B、 C、 或 D、 或5. 将一副直角三角尺按如图所示摆放,则图中 的度数是( )
A、 B、 C、 或 D、 或5. 将一副直角三角尺按如图所示摆放,则图中 的度数是( )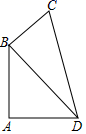 A、105° B、120° C、135° D、150°6. 如图,直线AB和CD相交于O,那么图中 ∠DOE与∠COA 的关系是( )
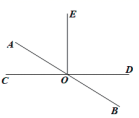
A、105° B、120° C、135° D、150°6. 如图,直线AB和CD相交于O,那么图中 ∠DOE与∠COA 的关系是( )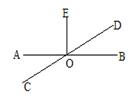 A、对顶角 B、相等 C、互余 D、互补7. 如图,下列说法中错误的是( ).
A、对顶角 B、相等 C、互余 D、互补7. 如图,下列说法中错误的是( ).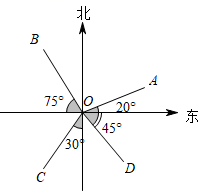 A、 方向是北偏东20° B、 方向是北偏西15° C、 方向是南偏西30° D、 方向是东南方向8. 下列画图语句中,正确的是( )A、画射线OP=3 cm B、画出A、B两点的距离 C、延长射线OA D、连接A、B两点9. 在下图中,∠1和∠2是对顶角的是( )A、
A、 方向是北偏东20° B、 方向是北偏西15° C、 方向是南偏西30° D、 方向是东南方向8. 下列画图语句中,正确的是( )A、画射线OP=3 cm B、画出A、B两点的距离 C、延长射线OA D、连接A、B两点9. 在下图中,∠1和∠2是对顶角的是( )A、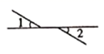 B、
B、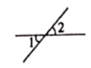 C、
C、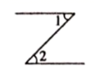 D、
D、 10. 现实生活中“为何有人宁可违反交通规则翻越隔离带乱穿马路,也不愿从天桥或斑马线通过?”,请用数学知识解释这一现象,其原因为( )A、两点之间线段的长度,叫做这两点之间的距离 B、过一点有无数条直线 C、两点确定一条直线 D、两点之间,线段最短11. 已知:如图,AB⊥CD,垂足为O,EF为过点O的一条直线,则∠1与∠2的关系一定成立的是( )
10. 现实生活中“为何有人宁可违反交通规则翻越隔离带乱穿马路,也不愿从天桥或斑马线通过?”,请用数学知识解释这一现象,其原因为( )A、两点之间线段的长度,叫做这两点之间的距离 B、过一点有无数条直线 C、两点确定一条直线 D、两点之间,线段最短11. 已知:如图,AB⊥CD,垂足为O,EF为过点O的一条直线,则∠1与∠2的关系一定成立的是( )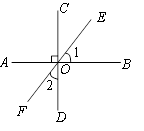 A、相等 B、互余 C、互补 D、不确定12. 如图,已知射线OA⊥射线OB, 射线OA表示北偏西25°的方向,则射线OB表示的方向为( )
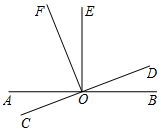
A、相等 B、互余 C、互补 D、不确定12. 如图,已知射线OA⊥射线OB, 射线OA表示北偏西25°的方向,则射线OB表示的方向为( )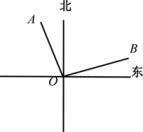 A、北偏东65° B、北偏东55° C、北偏东75° D、东偏北75°13. 如图,由点O测点A的方向是( )
A、北偏东65° B、北偏东55° C、北偏东75° D、东偏北75°13. 如图,由点O测点A的方向是( )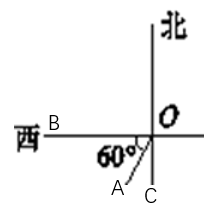 A、北偏南60° B、南偏西60° C、南偏西30° D、西偏南30°
A、北偏南60° B、南偏西60° C、南偏西30° D、西偏南30°二、填空题
-
14. 已知 .则 的余角为.15. 若 ,则 的补角等于 .16. 钟表上显示6时20分,则此刻时针与分针的夹角的度数为 .17. 基本事实:已知过 两点可以画一条直线 ,我们得到了一个基本事实 , 若平面内有不在同一直线上的3个点,过其中任意两点,一共可以画条直线;
类比:如图 ,已知 ,在AOB的内部画射线 ,则图中共有个角;
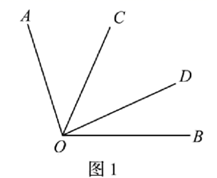
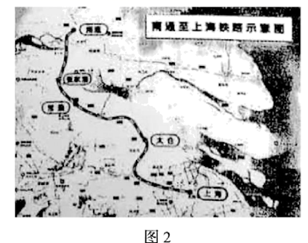
实践应用:2020年7月1日,沪苏通铁路正式通车,加快了长三角交通一体化建设,沪苏通铁路衔接南通和上海,并在沿途增设张家港、常熟、太仓三个停靠站,如图2.若一动车往返于上海与南通之间,已知各站之间的路程均不相等.则共有种不同的票价.(不考虑座位等级等其它因素)
 18. 如图,直线 、 相交于点 ,将量角器的中心与点 重合,发现表示 的点在直线 上,表示 的点在直线 上,则 .
18. 如图,直线 、 相交于点 ,将量角器的中心与点 重合,发现表示 的点在直线 上,表示 的点在直线 上,则 .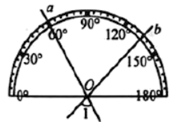 19. 如图,将一个三角板 角的顶点与另一个三角板的直角顶点重合, , .
19. 如图,将一个三角板 角的顶点与另一个三角板的直角顶点重合, , .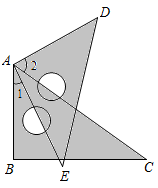 20. 已知 ,则 的补角是.21. 如图,将四边形ABCD沿虚线裁去一个角得到五边形ABCFE , 则该五边形的周长原四边形的周长(填“大于”、“小于”或“等于”).
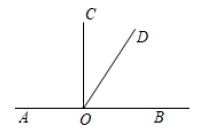
20. 已知 ,则 的补角是.21. 如图,将四边形ABCD沿虚线裁去一个角得到五边形ABCFE , 则该五边形的周长原四边形的周长(填“大于”、“小于”或“等于”).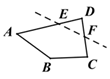 22. 如图,∠1=30°,则射线OA表示的方位是南偏东.
22. 如图,∠1=30°,则射线OA表示的方位是南偏东.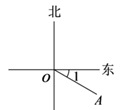 23. 从甲地到乙地有3条路,但小明说这三条路都不是最短的,小明的依据是.
23. 从甲地到乙地有3条路,但小明说这三条路都不是最短的,小明的依据是. 24. 已知 ,则 的补角等于 .25. 时钟上 点 分时,时针与分针的夹角为.26. 下列生产和生活现象:①用两个钉子就可以把木条固定在墙上;②把弯曲的公路改直,就能缩短路程;③植树时,只要确定两棵树的位置,就能确定同一行树所在的直线;④从 地到 地架设电线,总是尽可能沿着线段 架设.其中能用“两点之间,线段最短”来解释的现象有.(填序号)27. 如图,直线 , 相交于点 , ,垂足为点 ,若 ,则 的度数为.
24. 已知 ,则 的补角等于 .25. 时钟上 点 分时,时针与分针的夹角为.26. 下列生产和生活现象:①用两个钉子就可以把木条固定在墙上;②把弯曲的公路改直,就能缩短路程;③植树时,只要确定两棵树的位置,就能确定同一行树所在的直线;④从 地到 地架设电线,总是尽可能沿着线段 架设.其中能用“两点之间,线段最短”来解释的现象有.(填序号)27. 如图,直线 , 相交于点 , ,垂足为点 ,若 ,则 的度数为.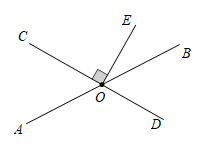 28. 已知 ,则 的补角是°'.29. 已知 ,那么 的补角等于.30. “数形结合”思想在数轴上得到充分体现,如在数轴上表示数5和 的两点之间的距离,可列式表示为 ,或 ;表示数 和 的两点之间的距离可列式表示为 .已知 ,则 的最大值为.31. 如图,某海域有三个小岛 , , ,在小岛处观测到小岛 在它北偏东 的方向上,观测到小岛 在它南偏东 的方向上,则 的补角的度数是.
28. 已知 ,则 的补角是°'.29. 已知 ,那么 的补角等于.30. “数形结合”思想在数轴上得到充分体现,如在数轴上表示数5和 的两点之间的距离,可列式表示为 ,或 ;表示数 和 的两点之间的距离可列式表示为 .已知 ,则 的最大值为.31. 如图,某海域有三个小岛 , , ,在小岛处观测到小岛 在它北偏东 的方向上,观测到小岛 在它南偏东 的方向上,则 的补角的度数是.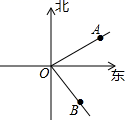 32. 已知∠α与∠β互为补角,且∠β比∠α大20°,则∠α的度数是.33. 一个角的补角加上 后,等于这个角的余角的4倍,则这个角等于 .34. 已知∠α=50°46′,则∠α的余角为.35. 一个角的度数是 ,则它的补角的度数为.
32. 已知∠α与∠β互为补角,且∠β比∠α大20°,则∠α的度数是.33. 一个角的补角加上 后,等于这个角的余角的4倍,则这个角等于 .34. 已知∠α=50°46′,则∠α的余角为.35. 一个角的度数是 ,则它的补角的度数为.三、解答题
-
36. 一个角的余角比它的补角的 还少15°,求这个角的度数.37. 一个角的余角与这个角的补角的和比平角的 多1°,求这个角.38. 如图,点 在直线 上, , ,求 的度数.
 39. 如图,直线AB、CD、EF相交于点O,∠DOB是它的余角的2倍,∠AOE=2∠DOF,且有OG⊥AB,求∠EOG的度数.
39. 如图,直线AB、CD、EF相交于点O,∠DOB是它的余角的2倍,∠AOE=2∠DOF,且有OG⊥AB,求∠EOG的度数.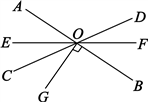
四、综合题