初中数学苏科版七年级上册第四章一元一次方同步练习卷2-填空解答

试卷更新日期：2021-06-22 类型：同步测试

进入出卷网下载

一、填空题

1. 已知x＝1是方程ax－5＝3a+3的解，则a＝．

查看试题解析
2. 已知 $x = 1$ 是方程 $2 a x - 5 = a + 3$ 的解，则 $a =$ ．

查看试题解析
3. 已知关于 $x$ 的一元一次方程 $\frac{x}{2019} + 3 = 2019 x + m$ 的解为 $x = 2$ ，那么关于 $x$ 的一元二次方程 $\frac{1 - y}{2019} + 2019 (y - 1) = m - 3$ 的解 $y$ = ．

查看试题解析
4. 已知 $x = 1$ 是关于 $x$ 的方程 $2 x - m = 3$ 的解，则代数式 $m$ = ．

查看试题解析
5. 若 $x = 2$ 是关于 $x$ 的方程 $m x - 4 = 3 m$ 的解，则 $m$ ＝.

查看试题解析
6. 若 $x = - 2$ 是关于x的方程 $\frac{2 + a}{3} = x$ 的解，则a的值为．

查看试题解析

二、解答题

7. 当m为何值时，关于x的方程2（2x-m）=2x-（-x+1）的解是方程x-2=m的解的3倍？

查看试题解析
8. m为何值时，关于x的方程4x-2m=3x-1的解与x=2x-3m的解互为相反数

查看试题解析
9. 某同学在计算－4－N时，误将－N看成了＋N，从而算得结果是5.请你帮助算出正确结果.

查看试题解析
10. 2020年2月，为了应对武汉发生的新型冠状病毒疫情，国家卫健委及相关单位在武汉建立了方舱医院，某方舱医院的具体信息如下：
（ 1 ）方舱医院由四部分组成，分别是废弃物处理单元、病房单元、技术保障单元、医疗功能单元；

（ 2 ）整个方舱医院占地面积为80000平方米；

（ 3 ）废弃物处理单元面积为总占地面积的5%；

（ 4 ）病房单元占地面积是技术保障单元占地面积的4倍；

（ 5 ）病房单元与医疗功能单元面积的和不高于总占地面积的85%，求医疗功能单元的最大面积.

查看试题解析
11. 不论 $x$ 取何值，等式 $a x - b - 4 x = 3$ 永远成立，求 $\frac{1}{2} a b$ 的值.

查看试题解析

三、综合题

12. 甲、乙两班学生到水果超巿购买桔子，已知桔子的价格如下表：

购桔子千克数

不超过5千克

超过5千克但不超过10千克

超过10千克

每千克价格

6元

5元

4元

甲班分两次共购买桔子40千克（第二次多于第一次），共付出168元；而乙班则一次购买桔子40千克.

(1)、乙班比甲班少付出元；

(2)、甲班第一次、第二次分别购买多少千克？（用方程求解）

查看试题解析
13. “丰收1号”油菜籽的平均每公顷产量为2400千克，含油率为45%.“丰收2号”油菜籽比“丰收1号”的平均每公顷产量提高了300千克，含油率提高了5个百分点.光明村去年种植“丰收1号”油菜，今年改种“丰收2号”油菜，并且种植面积比去年减少3公顷.

(1)、若今年所产油菜籽的总产油量与去年的总产油量相等，求该村去年种植油菜的面积；

(2)、若今年所产油菜籽的总产油量比去年提高2160千克，求该村今年种植油菜的面积.

查看试题解析
14. 已知 $k \neq 0$ ，将关于 $x$ 的方程 $k x + b = 0$ 记作方程☆.

(1)、当 $k = 3$ ， $b = - 2$ 时，方程☆的解为.

(2)、若方程☆的解为 $x = - 5$ ，写出一组满足条件的 $k$ ， $b$ 值：k＝， b＝；

(3)、若方程☆的解为 $x = 3$ ，求关于 $y$ 的方程 $k (2 y - 5) - b = 0$ 的解.

查看试题解析
15. 已知： $y_{1} = x + a, y_{2} = - x + b$ ，

(1)、当 $a = 3, b = 2$ 时，x取何值， $y_{1}$ 的值比 $y_{2}$ 的2倍大5？

(2)、若 $y_{1} = - 5, y_{2} = 11$ ，求 $a + b$ 的值.

查看试题解析
16. 已知，两正方形在数轴上运动，起始状态如图所示.A、F表示的数分别为-2、10，大正方形的边长为4个单位长度，小正方形的边长为2个单位长度，两正方形同时出发，相向而行，小正方形的速度是大正方形速度的两倍，两个正方形从相遇到刚好完全离开用时2秒.完成下列问题：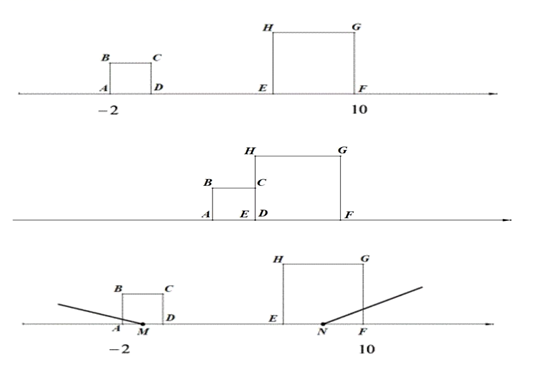

(1)、求起始位置D、E表示的数；

(2)、求两正方形运动的速度；

(3)、M、N分别是AD、EF中点，当正方形开始运动时，射线MA开始以15°/s的速度顺时针旋转至MD结束，射线NF开始以30°/s的速度逆时针旋转至NE结束，若两射线所在直线互相垂直时，求MN的长.

查看试题解析
17. 小明和父母打算去某火锅店吃火锅，该店在网上出售“ $25$ 元抵 $50$ 元的全场通用代金券”(即面值 $50$ 元的代金券实付 $25$ 元就能获得)，店家规定代金券等同现金使用，一次消费最多可用 $3$ 张代金券，而且使用代金券的金额不能超过应付总金额.

(1)、如果小明一家应付总金额为 $145$ 元，那么用代金券方式买单，他们最多可以优惠多少元:

(2)、小明一家来到火锅店后，发现店家现场还有一个优惠方式: 除锅底不打折外，其余菜品全部 $6$ 折.小明一家点了一份 $50$ 元的锅底和其他菜品，用餐完毕后，聪明的小明对比两种优惠，选择了现场优惠方式买单，这样比用代金券方式买单还能少付 $15$ 元.问小明一家实际付了多少元?

查看试题解析
18. 甲、乙两班学生到集市上购买苹果，苹果的价格如下：

购苹果数

不超过10千克

超过10千克但不超过20千克

超过20千克

每千克价格

10元

9元

8元

甲班分两次共购买苹果30千克（第二次多于第一次），共付出256元；而乙班则一次购买苹果30千克.

(1)、乙班比甲班少付出多少元？

(2)、设甲班第一次购买苹果x千克.
①则第二次购买的苹果为多少千克；

②甲班第一次、第二次分别购买多少千克？

查看试题解析
19. 已知方程6x－9＝10x－45与方程3a－1＝3（x＋a）－2a的解相同.

(1)、求这个相同的解；

(2)、求a的值；

(3)、若[m]表示不大于m的最大整数，求[－ $\frac{1}{3}$ a－2]的值.

查看试题解析
20. 已知方程 $(3 m - 4) x^{2} - (5 - 3 m) x - 4 m = - 2 m$ 是关于 $x$ 的一元一次方程.

(1)、求 $m$ 和 $x$ 的值.

(2)、若 $n$ 满足关系式 $| 2 n + m | = 1$ ，求 $n$ 的值.

查看试题解析
21. 为了方便市民出行，减轻城市中心交通压力，南通市正在修建贯穿城市的地铁1，2号线，已知修建地铁1号线24千米和2号线22千米共需投资265亿元；若1号线每千米的平均造价比2号线每千米的平均造价多 $0.5$ 亿元.

(1)、求1号线、2号线每千米的平均造价.

(2)、除1，2号线外，南通市政府规划还要再建90千米的地铁网线 $.$ 根据预算，这90千米的地铁网线每千米的平均造价是1号线每千米的平均造价的 $1.2$ 倍，则还需投资多少亿元？

查看试题解析
22. 对于三个数a，b，c，用 $M {a,$ b， $c}$ 表示a，b，c这三个数的平均数，用 $m i n {a,$ b， $c}$ 表示a，b，c这三个数中最小的数，如： $M {- 1,$ 2， $3} = \frac{- 1 + 2 + 3}{3} = \frac{4}{3}$ ， $m i n {- 1,$ 2， $3} = - 1$ .

(1)、若 $M {x - 1, - 5, 2 x + 3} = \frac{1}{2} (1 + 3 x)$ ，求x的值；

(2)、已知 $M {2 x, - x + 2, 3}$ ， $m i n {- 1,$ 0， $4 x + 1}$ ，是否存在一个x值，使得 $2 \times M {2 x, - x + 2, 3} = m i n {- 1,$ 0， $4 x + 1} .$ 若存在，请求出x的值；若不存在，请说明理由.

查看试题解析
23. 暑假期间，小明和小颖两家共8人相约外出旅行，分别乘坐两辆出租车前往机场在距离机场11千米处一辆车出了故障不能继续行驶.此时离机场停止办理登机手续还有30分钟，唯一可以利用的交通工具只有另一辆出租车，连同司机在内限乘5人，车速每小时60千米.

(1)、如果这辆车分两批接送，其中4人乘车先走，余下4人原地等候，8人能否及时到达机场办理登机手续？(上下车时间忽略不计)

(2)、如果这辆车在送第一批客人的时候，余下的人以每小时6千米的速度步行前往机场，待司机将第一批客人送达后立即返回接第二批客人，他们能及时到达机场吗？

查看试题解析
24. 解下列方程：

(1)、 x-4=2-5x

(2)、5(x+8)=6(2x−7)+5

(3)、6+ $\frac{x}{3}$ = $\frac{8 - 2 x}{2}$

(4)、 $\frac{0 \cdot 2 - x}{0 \cdot 3}$ -1= $\frac{0 \cdot 1 + x}{0 \cdot 2}$

查看试题解析
25. 解方程：

(1)、3（x+2）﹣1=x﹣3；

(2)、 $\frac{x + 1}{2}$ ﹣1= $\frac{2 - x}{3}$ ．

查看试题解析
26. 解下列方程：

(1)、 $\frac{x + 1}{2} = \frac{4}{3} x + 1$

(2)、 $\frac{2 x - 1}{3} = \frac{2 x + 1}{6} - 1$ ．

查看试题解析
27. 解方程：

(1)、3﹣2（x﹣1）=5x

(2)、2﹣ $\frac{2 x + 1}{3}$ = $\frac{1 + x}{2}$ ．

查看试题解析
28. 解方程：

(1)、3（x+1）=9；

(2)、 $\frac{2 x - 1}{3}$ =1﹣ $\frac{2 x - 1}{6}$ ．

查看试题解析
29. 解方程：

(1)、2（x+8）=3x﹣3；

(2)、 $\frac{x + 1}{2}$ ﹣1=2﹣ $\frac{x - 2}{4}$ ．

查看试题解析
30. 解方程：

(1)、2（x﹣1）+1=0；

(2)、 $\frac{1}{3}$ x﹣1= $\frac{x - 3}{2}$ ．

查看试题解析
31. 解方程：

(1)、4x﹣3（5﹣x）=6

(2)、 $\frac{2 x + 1}{3} - \frac{x - 1}{6} = 2$

查看试题解析
32. 解方程

(1)、2x﹣1=3

(2)、2（3﹣x）=﹣4x+5

(3)、 $\frac{x - 1}{4}$ = $\frac{2 x + 1}{6}$ +1．

查看试题解析
33. 解方程：

(1)、4（2x﹣3）﹣（5x﹣1）=7

(2)、 $\frac{2 x - 1}{3}$ ﹣ $\frac{5 - x}{6}$ =﹣2

(3)、2x﹣ $\frac{1}{2}$ [x﹣ $\frac{1}{2}$ （x﹣1）]= $\frac{2}{3}$ （x﹣1）

(4)、 $\frac{0.1 - 2 x}{0.3}$ =1+ $\frac{x}{0.15}$ ．

查看试题解析
34. 阅读理解：
在解形如3|x﹣2|=|x﹣2|+4这一类含有绝对值的方程时，我们可以根据绝对值的意义分x＜2和x≥2两种情况讨论：
①当x＜2时，原方程可化为﹣3（x﹣2）=﹣（x﹣2）+4，解得：x=0，符合x＜2
②当x≥2时，原方程可化为3（x﹣2）=（x﹣2）+4，解得：x=4，符合x≥2
∴原方程的解为：x=0，x=4．
解题回顾：本题中2为x﹣2的零点，它把数轴上的点所对应的数分成了x＜2和x≥2两部分，所以分x＜2和x≥2两种情况讨论．
知识迁移：

(1)、运用整体思想先求|x﹣3|的值，再去绝对值符号的方法解方程：|x﹣3|+8=3|x﹣3|；
知识应用：

(2)、运用分类讨论先去绝对值符号的方法解类似的方程：|2﹣x|﹣3|x+1|=x﹣9．
提示：本题中有两个零点，它们把数轴上的点所对应的数分成了几部分呢？

查看试题解析
35. 阅读下列解方程的过程，并完成（1）、（2）小题的解答．
解方程：|x﹣1|=2
解：当x﹣1＜0，即x＜1时，原方程可化为：﹣（x﹣1）=2，解得x=﹣1；当x﹣1≥0，即x≥1时，原方程可化为：x﹣1=2，解得x=3；
综上所述，方程|x﹣1|=2的解为x=﹣1或x=3．

(1)、解方程：|2x+3|=8

(2)、解方程：|2x+3|﹣|x﹣1|=1．

查看试题解析
36. 已知梯形的面积公式为S= $\frac{(a + b) h}{2}$

(1)、把上述的公式变形成已知S，a，b，求h的公式

(2)、若a：b：S=2：3：4，求h的值．

查看试题解析
37. （4﹣n²）x²﹣（n﹣2）x﹣8=0是关于x的一元一次方程，

(1)、试求x值

(2)、求关于y方程n+|y|=x的解．

查看试题解析
38. 计算题

(1)、解方程：2（y+6）=4﹣2（2y﹣1）

(2)、解方程： $\frac{x + 1}{3} - \frac{2 - 3 x}{2} = 2$ ．

查看试题解析
39. 根据等式性质．回答下列问题；

(1)、从ab=bc能否得到a=c．为什么？

(2)、从 $\frac{a}{b}$ = $\frac{c}{b}$ 能否得到a=c，为什么？

(3)、从ab=1能否得到a+1= $\frac{1}{b}$ +1，为什么？

查看试题解析
40. 观察下列变形：
∵x=1，①
∴3x﹣2x=3﹣2，②
∴3x﹣3=2x﹣2，③
∴3（x﹣1）=2（x﹣1），④
∴3=2．⑤

(1)、由②到③这一步是怎样变形的？

(2)、发生错误的变形是哪一步？其原因是什么？

查看试题解析

购桔子千克数	不超过5千克	超过5千克但不超过10千克	超过10千克
每千克价格	6元	5元	4元

购苹果数	不超过10千克	超过10千克但不超过20千克	超过20千克
每千克价格	10元	9元	8元

初中数学苏科版七年级上册第四章 一元一次方 同步练习卷2-填空解答

一、填空题

二、解答题

三、综合题

初中数学苏科版七年级上册第四章一元一次方同步练习卷2-填空解答