初中数学苏科版七年级上册3.3代数式的值同步练习

试卷更新日期：2021-06-22 类型：同步测试

进入出卷网下载

一、单选题

1. 代数式“m的两倍与n的平方差”，下列表示正确的是（）

A、2m²－n² B、（2m－n）² C、2m－n² D、（2m）²－n²

查看试题解析
2. 已知整式x²－2x＋6的值为9，则－2x²＋4x＋6的值（）

A、0 B、－2 C、1 D、－7

查看试题解析
3. 已知 ${(x - 2)}^{5} = a x^{5} + b x^{4} + c x^{3} + d x^{2} + e x + f$ ，求：a+b+c+d+e+f =（）

A、2 B、0 C、-1 D、－2

查看试题解析
4. 若多项式2x²+3x+7的值为10.则多项式6x²+9x-8的值为（）

A、1 B、2 C、3 D、4

查看试题解析
5. 当x=3时，代数式ax³+bx+2的值为1；则当x=-3时，代数式ax³+bx+2的值为（）

A、-3 B、-1 C、1 D、3

查看试题解析
6. 如果 $x - 2 y = 3$ ，那么 $2 x - 4 y + 5$ 的值等于（）

A、1 B、8 C、11 D、-1

查看试题解析
7. 若代数式 $2 x^{2} - 3 x + 1$ 的值是3，则代数式 $4 x^{2} - 6 x + 3$ 的值是（）

A、9 B、7 C、5 D、6

查看试题解析
8. 按如图的程序计算，若开始输入的x的值为3，则最后输出的结果是（）

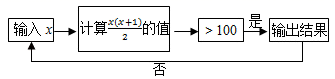A、156 B、6 C、231 D、23

查看试题解析
9. 某商品每件成本为a元，按成本增加50%定出价格，现由于库存积压减价，按定价的80%出售，现在每件商品的利润为（）

A、0.02a元 B、0.2a元 C、1.02a元 D、1.2a元

查看试题解析
10. 若多项式3x^|m|+（m﹣2）x+1是关于x的二次三项式，则m的值（）

A、2或﹣2 B、2 C、﹣2 D、﹣4

查看试题解析
11. 小颖按如图所示的程序输入一个正数x，最后输出的结果为94，则满足条件的x的不同值最多有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析

二、填空题

12. 有一计算程序如下：若输出的值是16，则 $x$ 的值是.

查看试题解析
13. 已知2a－b＋2＝0，则1－4a＋2b的值为.

查看试题解析
14. 已知 $x^{2} - 3 y + 2 = 0$ ，则 $2 (x^{2} - 3 y) + 5$ 的值为．

查看试题解析
15. 单项式 $- \frac{1}{3} a^{3} b c$ 的次数是．

查看试题解析
16. 已知 $a - 2 b = - 3$ ，则式子 $2021 - a + 2 b =$ ．

查看试题解析
17. 若 $2 x - 3 y + 2 = 0$ ，则 $5 - 4 x + 6 y =$ .

查看试题解析

18. 牛顿在他的《普遍的算术》一书中写道：“要解答一个含有数量间的抽象关系的问题，只要把题目由日常语言译成代数语言就行了.”请阅读下表，并填写表中空白.

日常语言	代数语言
连云港到南京的城际列车在连云港站出发时车上有一些乘客	$x$
到灌云站时无人下车，有10人上车	$x + 10$
到灌南站时有1人下车后，又有车上人数的 $\frac{1}{9}$ 人上车

查看试题解析

19. 如果 $2 a + b = 1$ ，那么 $4 a + 2 b - 1$ 的值等于.

查看试题解析
20. 数轴上三个点表示的数分别为 p、r、s.若 p-r＝5，s-p＝2，则 s-r 等于.

查看试题解析
21. 已知代数式2x-3y的值是3，则5-2x+3y的值是.

查看试题解析
22. 已知 $m - 2 n = - 2$ ，则 $5 - 2 m + 4 n$ 的值是.

查看试题解析
23. 已知 $2 a - 3 b = 2$ ，则 $8 - (6 a - 9 b)$ 的值是.

查看试题解析
24. 已知多项式（3﹣b）x⁵+x^a+x﹣6是关于x的二次三项式，则a²﹣b²的值为.

查看试题解析
25. 如图是一组数值转换机，若输入的 $x = - 3$ ，则输出的结果为.

查看试题解析
26. 一个两位数的十位数字是 $x$ ，个位上的数字是2，则这个两位数可表示成.（用含 $x$ 的代数式表示）.

查看试题解析
27. 单项式﹣ $\frac{2}{3}$ xy³的系数是m，次数是n，则mn＝.

查看试题解析
28. 如果x²-3x的值是-1，则代数式-3x²+9x-6的值是

查看试题解析
29. 计算：
$2 \times [3 \times (\frac{1}{7} + \frac{1}{8} + \frac{1}{9}) + 6 \times (\frac{1}{4} + \frac{1}{5} + \frac{1}{6}) + 1] - 3 \times [2 \times (\frac{1}{7} + \frac{1}{8} + \frac{1}{9}) + 4 \times (\frac{1}{4} + \frac{1}{5} + \frac{1}{6}) - 1]$ =.

查看试题解析
30. 已知当 $x = 2$ 时，代数式 $a x^{3} + b x + 2$ 的值为7，则当 $x = - 2$ 时，代数式 $a x^{3} + b x + 2$ 的值为.

查看试题解析
31. 已知 $m^{2} + 2 m n = 3$ ， $m n + n^{2} = 4$ ，则 $m^{2} - 2 n^{2}$ 的值为.

查看试题解析
32. 用16米长的篱笆围成长方形的生物园饲养小兔，如果生物园的宽为a米，则这个生物园的面积为平方米.

查看试题解析
33. 已知 $x^{2} - 2 y^{2} - 4 = 0$ ，则整式 $- 2 x^{2} + 4 y^{2} - 3 =$ .

查看试题解析
34. 小刚学学习了有理数运算法则后，编了一个计算程序，当他输入任意一个有理数时，显示屏上出现的结果总等于所输入的有理数的平方与1的和，当他第一次输入2，然后又将所得的结果再次输入后，显示屏上出现的结果应是.

查看试题解析

三、解答题

35. 已知a , b为常数，且三个单项式4xy² ， axy^b ， -5xy相加得到的和仍然是单项式。那么a和b的值可能是多少？说明你的理由。

查看试题解析

四、综合题

36. 下图是一个运算程序，

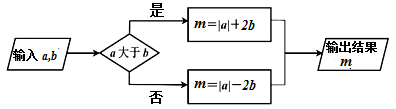(1)、当 $a = - 1$ ， $b = 2$ 时，求输出结果 $m$ ；

(2)、若 $a = 3$ ，输出结果 $m$ 与 $b$ 相等，求 $b$ 的值；

(3)、若输入非零有理数 $a$ ， $b$ 恰互为相反数，比较代数式 $2 a - 3 b + 4 m$ 的值与0的大小.

查看试题解析

37. 某超市在春节期间对顾客实行优惠，规定如下：

一次性购物	优惠办法
少于200元	不予优惠
低于500元但不低于200元	九折优惠
500元或超过500元	其中500元部分给予九折优惠，超过500元部分给予八折优惠

(1)、王老师一次性购物700元，他实际付款元．

(2)、若顾客在该超市一次性购物x元，当x小于500元但不小于200时，他实际付元，当x大于或等于500元时，他实际付款元．（用含x的代数式表示）．

(3)、如果王老师两次购物货款合计810元，第一次购物的货款为a元（200＜a＜300），用含a的代数式表示：两次购物王老师实际付款多少元？