初中数学苏科版七年级上册2.8 有理数混合运算同步练习

试卷更新日期：2021-06-22 类型：同步测试

进入出卷网下载

一、单选题

1. 如图所示为我市2021年1月11日的天气预报图，则这天的温差是（）

A、 $- 6 ° C$ B、 $- 2 ° C$ C、 $4 ° C$ D、 $6 ° C$

查看试题解析
2. 两个同样大小的正方体按如图的方式放在一起，每个正方体相对两个面上写的数字之和都等于0．现将两个正方体并排放置，看得见的5个面上的数如图所示，则看不见的7个面上所写的数字之和等于（）

A、-5 B、-7 C、5 D、无法确定

查看试题解析
3. 某商场举办“迎新春送大礼”的促销活动，全场商品一律打八折销售.小明买了一件商品，比标价少付了40元，那么他购买这件商品花了（）

A、80元 B、120元 C、160元 D、200元

查看试题解析
4. 下列各数中，比 $| - 2 |$ 小5的数是（）

A、-7 B、-3 C、3 D、7

查看试题解析
5. 如图所示是计算机某计算程序，若开始输入x＝－2，则最后输出的结果是（）

A、－4 B、－10 C、－6 D、－12

查看试题解析

二、填空题

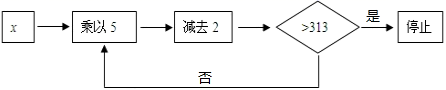
6. 一个蓄水池有甲、乙两个进水管，单独开甲管20小时可以注满水池，单独开乙管12小时可以注满水池，那么两管齐开注满水池，需要小时.

查看试题解析
7. 输入x，按如图所示程序进行运算：规定：程序运行到“判断大于313”计为一次运算.若输入的x为8，则程序运算次停止.

查看试题解析
8. 一次数学测试，如果 $95$ 分为优秀，以 $95$ 分为基准简记，例如 $106$ 分记为 $+ 11$ 分，那么 $86$ 分应记为分.

查看试题解析
9. 中国奇书《易经》中记载，远古时期，人们通过在绳子上打结来计数，即“结绳计数”.如图，一位母亲在从右到左依次排列的绳子上打结，满5进 $1$ ，用来记录孩子自出生后的天数.由图可知，孩子自出生后的天数是.

查看试题解析
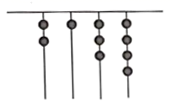10. $A$ 地的海拔高度是 $51 m$ ， $B$ 地的海拔高度是 $- 14 m$ ， $C$ 地的海拔高度是 $- 105 m$ ，则 $A$ ， $B$ ， $C$ 三地中，地势最高的地方比地势最低的地方高 $m$ .

查看试题解析
11. 世界上大部分国家都使用摄氏（℃）温度，但美、英等国的天气预报仍然使用华氏（F）温度. 两种计量之间有如下对应：f=1.8t+32（f表示华氏温度，t表示摄氏温度），那么摄氏5度相当于华氏度.

查看试题解析
12. 钢笔m元/支，笔记本2m元/本，小刚买了3支钢笔和5本笔记本，共用去元.

查看试题解析
13. ${(- 1)}^{2 n} + {(- 1)}^{2 n + 1}$ =(n为正整数).

查看试题解析
14. 如下图是一个数值运算程序，当输入值为 -5时，则输出的数值为．

查看试题解析
15. 计算： ${(- 1)}^{1} + {(- 1)}^{2} + {(- 1)}^{3} + {(- 1)}^{4} + \dots + {(- 1)}^{1000} + {(- 1)}^{1001} =$

查看试题解析
16. 将2，-7，1，-5这四个数（都用且只能用一次）进行“ $+, -, \times, \div$ ”运算，可加括号，使其结果等于24，写出其中的一种算法：．

查看试题解析
17. 计算：2×4﹣2+4＝．

查看试题解析
18. 如图所示是计算机某计算程序，若开始输入x=﹣2，则最后输出的结果是

查看试题解析
19. 小丽计划在某外卖网站点如下表所示的菜品.已知每份订单的配送费为 5元，商家为了促销，对每份订单的总价（不含配送费）提供满减优惠：满30元减12元，满70元减30元，满100元减40元.如果小丽在购买下表中的所有菜品时，采取适当的下订单方式，那么他点餐的总费用最低可为元.

查看试题解析
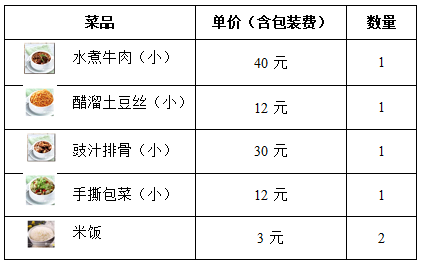20. 请你用运算符号（包括括号）把2，－6，－9，9 四个数写出一个算式，使它的结果等于24.那么你所列的式子为=24.

查看试题解析
21. 如图，方格表中的格子填上了数，每一行每一列及两条对角线中所填数的和均相等，则x的值是.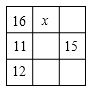

查看试题解析

三、计算题

22. 计算： $- \frac{1}{9} \times | 1 - {(- 2)}^{3} | - (\frac{1}{8} - \frac{2}{3}) \times 24$

查看试题解析
23. 计算；

(1)、 $- 1^{2020} + {(- 5)}^{2} - | - 3 |$

(2)、 $- \frac{1}{9} \times | 1 - {(- 2)}^{3} | - (\frac{1}{8} - \frac{2}{3}) \times 24$

查看试题解析
24. 计算：

(1)、 $2 \times {(- 3)}^{3} - 4 \times (- 3)$ ；

(2)、 $- 2^{2} \div (\frac{1}{2} \div \frac{1}{3}) \times (- \frac{5}{8})$ .

查看试题解析
25. 计算：

(1)、 $- 72 \times (\frac{1}{6} - \frac{3}{4} + \frac{5}{12})$

(2)、 $- 2^{4} \div 4 + (1 - \frac{1}{3}) \times | - 6 |$

查看试题解析
26. 计算：

(1)、 $(- 0.5) - | - 2.5 |$

(2)、 $- 1^{4} - 2 \times {(- 3)}^{2} \div \frac{1}{6}$

查看试题解析
27. 计算：

(1)、2×（-3）³-4×（-3）

(2)、-2²÷（ $\frac{1}{2}$ - $\frac{1}{3}$ ）×（- $\frac{5}{8}$ ）

查看试题解析
28. 计算：

(1)、（-2）³+ $\frac{1}{2}$ ×8.

(2)、 ${(- 2)}^{2} - | - 7 | + 3 - 2 \times (- \frac{1}{2})$

查看试题解析
29. 观察 $\frac{1}{1 \times 2}$ + $\frac{1}{2 \times 3}$ =（1－ $\frac{1}{2}$ ）+（ $\frac{1}{2}$ － $\frac{1}{3}$ ）=1－ $\frac{1}{3}$ = $\frac{2}{3}$

(1)、计算： $\frac{1}{1 \times 2}$ + $\frac{1}{2 \times 3}$ + $\frac{1}{3 \times 4}$ +……+ $\frac{1}{2013 \times 2014}$ =

(2)、计算： $\frac{1}{1 \times 3} + \frac{1}{3 \times 5} + \frac{1}{5 \times 7} + \dots \dots + \frac{1}{99 \times 101}$

查看试题解析

四、解答题

30. 8袋大米，以每袋50千克为准，超过的千克记作正数，分别为：－2、+1、+4、+6、－3、－4、+5、－3，求8袋大米共重多少千克？

查看试题解析

五、综合题

31. 食品厂从袋装食品中抽出样品30袋，检测每袋的质量是否符合标准.超过和不足的部分分别用正、负数表示，记录如下：

与标准质量的差值

（单位：克）

-4

-2

0

1

2

3

袋数

3

4

4

8

6

5

(1)、这批样品的平均质量比每袋的标准质量多（或少）多少克？

(2)、食品袋中标有“净重100±2克”，这批抽样食品中共有几袋质量不合格？这批抽样食品的总质量是多少？

查看试题解析
32. 网购的盛行，带动了快递行业的快速发展.一天快递员小李骑车从快递公司出发，在一条东西方向的马路上来回送件，规定在快递公司东边记为正，快递公司西边记为负，小李一天所走的路程记录如下：（单位：千米）：+4，－3，+5，－2.5，2.5，－3，－2.8，+1.5，+1.5，－1.2.

(1)、该快递员最后到达的地方在快递公司的哪个方向？距快递公司多远？

(2)、该快递员在这次送件过程中，共走了多少千米？

查看试题解析

33. 今年的“十•一，黄金周是7天的长假，花果山在7天假期中每天旅游人数变化如表（正号表示人数比前一天多，负号表示比前一天少），若9月30日的游客人数为0.2万人，

日期	1日	2日	3日	4日	5日	6日	7日
人数变化（单位：万人）	+1.8	-0.6	+1.2	-0.7	-0.3	+0.5	-0.7

问：

(1)、10月4日的旅客人数为万人；

(2)、七天中旅客人数最多的一天比最少的一天多万人；

(3)、如果每万人带来的经济收入约为100万元，则黄金周七天的总收入约为多少万元？

查看试题解析

34. 某天上午，一出租车司机始终在一条南北走向的笔直马路上营运.（出发点记作为点O，约定向南为正，向北为负）.期间一共运载6名乘客，行车里程(单位：千米)依先后次序记录如下：+7，-3，+6，-1，+2，-4.

(1)、出租车在行驶过程中，离出发点O最远的距离是千米；

(2)、将最后一名乘客送到目的地，出租车离出发点O多远？在O点的什么方向？

(3)、出租车收费标准为：起步价(不超过3千米)为10元，超过3千来的部分每千米的价格为1.6元，求司机这天上午的营业额.

查看试题解析

35. 有20袋大米，以每袋30千克为标准，超过的千克数用正数表述，不足的千克数用负数表述，具体称重记录如下：

与标准质量的差值（单位：千克）	-3	1	0	2.5	-2	-1.5
代数	1	2	3	8	4	2

(1)、20袋大米中，最重的一袋比最轻的一袋重千克；

(2)、与标准重量比较，

20

袋大米总计超过多少千克或不足多少千克？

(3)、若大米每千克售价3.5元，出售这20袋大米可卖多少元？

查看试题解析

36. 小明从家出发沿一条直道跑步，到达某一地点再原路返回，总共用15分钟回到家中.设小明出发t分钟时的速度为每分钟v 米， v与t之间的关系如下表.

t（分钟）

0＜t≤2

2＜t≤10

10＜t≤15

v（米/分钟）

100

150

40

(1)、小明跑步过程中与家的最远距离为米；

(2)、当2＜t≤10时，写出小明与家的距离；（用含t的代数式表示）

(3)、当t的值为时，小明与家的距离是160米.

查看试题解析

37. 某自行车厂计划一周生产自行车1400辆，平均每天生产200辆，但由于种种原因，实际每天生产量与计划量相比有出入。下表是某周的生产情况（超产记为正、减产记为负）:

星期	一	二	三	四	五	六	日
增减	+5	－2	－4	＋12	－10	＋16	－9

(1)、根据记录的数据可知该厂星期六生产自行车辆；

(2)、根据记录的数据可知该厂本周实际生产自行车辆；

(3)、产量最多的一天比产量最少的一天多生产自行车辆；

(4)、该厂实行每周计件工资制，每生产一辆车可得50元，若超额完成任务，则超过部分每辆另奖15元；少生产一辆扣20元，那么该厂工人这一周的工资总额是多少元？

查看试题解析

38. 某特技飞行队在名胜风景旅游区—张家界天门洞特技表演，其中一架飞机起飞后的高度变化如左下表：

(1)、此时这架飞机比起飞点高了多少千米？

(2)、如果飞机每上升或下降1千米需消耗2升燃油，那么这架飞机在这4个动作表演过程中，一共消耗了多少升燃油？

(3)、如果飞机做特技表演时，有4个规定动作，起飞后高度变化如下：上升3.8千米，下降2.9千米，再上升1.6千米.若要使飞机最终比起飞点高出1千米，问第4个动作是上升还是下降，上升或下降多少千米？

高度变化	记作
上升4.5 km	+4.5 km
下降3.2 km	-3.2km
上升1.1 km	+1.1km
下降1.4 km	-1.4km

查看试题解析

39. 随着手机的普及，微信（一种聊天软件）的兴起，许多人抓住这种机会，做起了“微商”，很多农产品也改变了原来的销售模式，实行了网上销售，这不刚大学毕业的小明把自家的冬枣产品也放到了网上，他原计划每天卖100斤冬枣，但由于种种原因，实际每天的销售量与计划量相比有出入，下表是某周的销售情况（超额记为正，不足记为负.单位：斤）；

星期	一	二	三	四	五	六	日
与计划量的差值	＋4	−3	−5	＋14	−8	＋21	−6

(1)、根据记录的数据可知前三天共卖出斤；

(2)、根据记录的数据可知销售量最多的一天比销售量最少的一天多销售斤；

(3)、若冬枣每斤按8元出售，每斤冬枣的运费平均3元，那么小明本周一共收入多少元？

查看试题解析

40. 某商店以每件200元的价格购进一批服装，加价40%后作为定价出售.

(1)、求该服装的售价是每件多少元？

(2)、“双十一”促销活动中，商店对该服装打八折，求每件服装的盈利率是多少？

查看试题解析

t（分钟）	0＜t≤2	2＜t≤10	10＜t≤15
v（米/分钟）	100	150	40

初中数学苏科版七年级上册2.8 有理数混合运算 同步练习

一、单选题

二、填空题

三、计算题

四、解答题

五、综合题

初中数学苏科版七年级上册2.8 有理数混合运算同步练习