初中数学苏科版七年级上册2.1-2.4 同步练习2-解答题

试卷更新日期：2021-06-22 类型：同步测试

进入出卷网下载

一、解答题

1. 将 $2$ ， $- \frac{3}{2}$ ， $0$ ， $5.34$ ， $\frac{1}{2}$ ， $π$ ， ${(- 2)}^{2}$ ， $- (- 3)$ ， $- 2^{2}$ 的整数在数轴上表示出来.

查看试题解析
2. 把下列各数在数轴上表示出来，并用“＜”连接各数.
0，+3， $- | - 2 |$ ， $- (- 4)$ ， $- 3 \frac{1}{2}$ .

查看试题解析
3. 在数轴上把下列各数表示出来，并用“＜”连接起来
$- 2 ， 2.5 ， | - 3 | ， - 3 \frac{1}{2}$

查看试题解析
4. 把下列各数表示的点画在数轴上，并用“＜”连接.
${(- 2)}^{2}$ ， $- | - 2 |$ ， $\frac{5}{2}$ ， $0$ ， $- (- 1)$ ， $- 3 \frac{1}{3}$ .

用“＜”把这些数连接起来： ▲ .

查看试题解析
5. 在数轴上画出表示下列各数的点，并用“＜”号将这些数按从小到大的顺序连接起来： $- 4.5$ ， $2.5$ ， $0$ ， $3.5$ ， $- 0.5$ ， $4$ .

查看试题解析
6. 把下列各数在数轴上表示出来，并用“＜”号连接
﹣1， +3， 0， ﹣（﹣2.5）， ﹣|﹣5|

查看试题解析
7. 把下列各数填入表示它所在的数集的括号里．
$- (- 2.3)$ ， $\frac{22}{7}$ ， 0 ， $- 2^{4}$ ， $30 %$ ，π ， $- | - 2013 |$ ， $- 5 \frac{1}{2}$   ， $0. \overset{\cdot}{3}$

负整数集合{               }

正有理数集合{           }

分数集合{                  }．

查看试题解析
8. 用数轴上的点表示下列各数，并用“<”将它们连起来：－5 $\frac{1}{2}$ ， $- | - 4 |$ ， 2， 0，－2 $\frac{1}{3}$

查看试题解析
9. 把下列各数分别填入相应的集合里：
﹣2， $1 \frac{1}{4}$ ， $- 5. \overset{•}{2}$ ，0， $\frac{π}{2}$ ，3.1415926， $- \frac{22}{7}$ ，+10％，2.626 626 662……，2020

正数集合 ${$                                 … $}$

负数集合 ${$                                  … $}$

整数集合 ${$                                  … $}$

分数集合 ${$                                  … $}$

无理数集合 ${$                                … $}$

查看试题解析

二、综合题

10. 有理数a、b、c，在数轴上的位置如图所示.

(1)、c0； $a + c$ 0；（用“＞、＜、=”填空）

(2)、化简： $| a + c | - | a - b | + | c |$

查看试题解析
11. 把下列各数填入相应的大括号中：
5.2，0， $\frac{π}{2}$ ， $\frac{22}{7}$ ，+（﹣4），﹣2 $\frac{3}{4}$ ，﹣（﹣3 ），0.25555…，﹣0.030030003…，

(1)、正数集合：{ …}

(2)、整数集合：{ …}

(3)、有理数集合：{…}．

查看试题解析
12.

(1)、请你在数轴上表示以下有理数： $- \frac{1}{2} ， | - 2.5 | ， 0 ， - (- 4)$

(2)、将上列各数用“<”号连接起来

查看试题解析
13.

(1)、请你在数轴上表示下列有理数：﹣5，|﹣1.5|，﹣ $\frac{5}{2}$ ，3 $\frac{1}{2}$ ，（﹣2）².

(2)、将上列各数用“<”号连接起来：.

查看试题解析
14. 把下列各数分别填入相应的集合里.
﹣5， $| - \frac{3}{2} |$ ，0，﹣3.14， $\frac{22}{7}$ ，﹣12.01001…，+1.99，﹣（﹣6），π

(1)、正数集合：{                …}

(2)、整数集合：{                  …}

(3)、分数集合：{               …}

(4)、无理数集合：{                  …}.

查看试题解析
15.

(1)、在数轴上表示下列各数：
（-2）² ， ﹣（﹣1），0，﹣|﹣3|，﹣4 $\frac{1}{2}$ .

(2)、把（1）中各数用“>”按照从大到小的顺序连接起来.

查看试题解析
16. 已知有理数a，b，c在数轴上对应的点的位置如图所示.

(1)、判断下列各式的符号： $a - b$ ， $b - c$ ， $c - a$ ；

(2)、若 $| a | = 2$ ， $| b | = \frac{1}{2}$ ， $| c | = 1$ ，试比较 $c - b$ 与 $b - a$ 之间的大小关系.

查看试题解析
17. 把下列各数填入相应集合的括号内： $2013, \frac{22}{7}, 3.1415926, 0, - 2 \frac{1}{3}, \frac{π}{4}, - | - 12 |, - 0.101001000...$

(1)、正数集合：{                                                 …}

(2)、负数集合：{                                                 …}

(3)、有理数集合：{                                               …}

(4)、无理数集合：{                                               …}

查看试题解析
18. 已知 $a$ ， $b$ ， $c$ 为有理数，且它们在数轴上的位置如图所示.

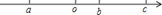(1)、试判断 $a$ ， $b$ ， $c$ 的正负性；

(2)、在数轴上标出 $a$ ， $b$ ， $c$ 相反数的位置；

(3)、若 $| a | = 5$ ， $| b | = 2.5$ ， $| c | = 7.5$ ，求 $a + b - c$ 的值.

查看试题解析
19. 如图，一只甲虫在5×5的方格（每小格边长为1）上沿着网格线运动.它从A处出发去看望B、C、D处的其它甲虫，规定：向上向右走为正，向下向左走为负.如果从A到B记为：A→B(+1，+4)，从B到A记为：B→A(-1，-4)，其中第一个数表示左右方向，第二个数表示上下方向．

(1)、图中A→C( ， )，B→C( ， )，C→(+1，)；

(2)、若这只甲虫从A处去甲虫P处的行走路线依次为（+2，+2），（+2，-1），（-2，+3），（-1，-2），请在图中标出P的位置；

(3)、若这只甲虫的行走路线为A→B→C→D，请计算该甲虫走过的路程；

(4)、若图中另有两个格点M、N，且M→A（3-a，b-4），M→N（5-a，b-2），则N→A应记为什么？

查看试题解析
20.

(1)、如图，两个圈分别表示负数集和分数集，请将3，0， $\frac{1}{2}$ ，－ $\frac{10}{3}$ ，－5，－3.4，π中，符合要求的数填入相应的圈中；

(2)、把下列各数 $- 2^{2}$ ， $- | - 3 |$ ， $+ (- \frac{1}{2})$ ， $- (- 2)$ ，在数轴上表示出来，并用“＞”把它们连接起来．

查看试题解析
21. 把下列各数序号分别填在表示它所在的集合里：
①﹣5，②﹣ $\frac{4}{5}$ ，③2.004×10² ， ④﹣（﹣4），⑤ $\frac{22}{7}$ ，⑥﹣|﹣13|，⑦﹣0.36，⑧0，⑨6.2，⑩ $\frac{π}{2}$

(1)、正数集合{                           …}；

(2)、负数集合{                           …}；

(3)、整数集合{                           …}；

(4)、分数集合{                           …}．

查看试题解析
22. 定义：若A，B，C为数轴上三点，若点C到点A的距离是点C到点B的距离2倍，我们就称点C是（A，B）的美好点.
例如：如图1，点A表示的数为 $- 1$ ，点B表示的数为2.表示1的点C到点A的距离是2，到点B的距离是1，那么点C是（A，B）的美好点；又如，表示0的点D到点A的距离是1，到点B的距离是2，那么点D就不是（A，B）的美好点，但点D是（B，A）的美好点.

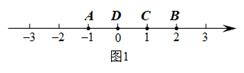
如图2，M，N为数轴上两点，点M所表示的数为 $- 7$ ，点N所表示的数为2.

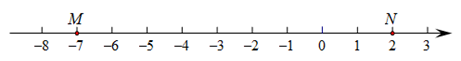
图2

备图

(1)、点E，F，G表示的数分别是 $- 3$ ，6.5，11，其中是（M，N）美好点的是；写出（N，M）美好点H所表示的数是.

(2)、现有一只电子蚂蚁P从点N开始出发，以2个单位每秒的速度向左运动. 当t为何值时，P，M和N中恰有一个点为其余两点的美好点？

查看试题解析
23.

(1)、画出数轴，并用数轴上的点表示下列各数；

(2)、用“＜”号把各数从小到大连起来．
﹣（﹣5），3，- $\frac{5}{2}$ ， 0，﹣|﹣3|， $- {(- 2)}^{2}$

查看试题解析
24. 同学们都知道， $| 4 - (- 2) |$ 表示4与-2的差的绝对值，实际上也可理解为4与-2两数在数轴上所对应的两点之间的距离，同理 $| x - 3 |$ 也可理解为 $x$ 与3两数在数轴上所对应的两点之间的距离， $| x + 1 | = | x - (- 1) |$ 就表示 $x$ 在数轴上对应的点到-1的距离，由上面绝对值的几何意义，解答下列问题：

(1)、求 $| 4 - (- 2) | =$ .

(2)、若 $| (x - 2) | = 5$ ，则 $x =$ .

(3)、请你找出所有符合条件的整数 $x$ ，使得 $| 1 - x | + | x + 2 | = 3$ .

(4)、求 $| x - 3 | + | x + 2 | + | x + 6 |$ 的最小值，并写出此时 $x$ 的取值情况.

(5)、已知 $| x - 1 | + | x + 2 | + | y - 3 | + | y + 4 | = 10$ ，求 $2 x + y$ 的最大值和最小值.

查看试题解析
25. 纽约、悉尼与上海的时差如下表（正数表示同一时刻比上海时间早的时数，负数表示同一时刻比上海晚的时数）：

城市

悉尼

纽约

时差/时

+2

﹣12

(1)、当上海是10月1日上午10时，悉尼时间是.

(2)、上海、纽约与悉尼的时差分别为（正数表示同一时刻比悉尼时间早的时数，负数表示同一时刻比悉尼晚的时数）

(3)、王老师2018年9月1日，从纽约Newwark机场，搭乘当地时间上午10：45的班机，前往上海浦东国际机场，飞机飞行的时间为14小时55分钟，问飞机降落上海浦东国际机场的时间.

查看试题解析
26. 小明骑车从家出发，先向东骑行2km到达A村，继续向东骑行3km到达B村.然后向西骑行9km 到达C村，最后回到家.

(1)、以家为原点.以向东方向为正方向.用1cm表示1km.画出数轴.并在数轴上表示出A、B、C三个村庄的位置.

(2)、C村离A村有多远？

(3)、小明一共行了多少km？

查看试题解析
27. 某面粉加工厂加工的面粉，用每袋可装10kg面粉的袋子装了200袋经过称重，质量超过标准质量10kg的用正数表示，质量低于标准质量10kg的用负数表示，结果记录如下
与标准质量的偏差(kg)
﹣1.5
﹣1
﹣0.5
0
0.5
1
2
袋数(袋)
40
30
10
25
40
20
35

(1)、求这批面粉的总质量；

(2)、如果100kg小麦加工80kg面粉，那么这批面粉是由多少千克小麦加工的？

查看试题解析
28. 已知，如图，A、B分别为数轴上的两点，A点对应的数为-20，B点对应的数为100.

(1)、请写出AB中点M对应的数。

(2)、现有一只电子蚂蚁P从B点出发，以6单位/秒的速度向左运动，同时另一只电子蚂蚁Q恰好从A点出发，以4单位/秒的速度向右运动。设两只电子蚂蚁在数轴上的C点相遇，你知道C点对应的数是多少吗？

(3)、若当电子蚂蚁P从B点出发时，以6单位/秒的速度向左运动，同时另一只电子蚂蚁Q恰好从A点出发，以4单位/秒的速度也向左运动。设两只电子蚂蚁在数轴上的D点相遇，你知道D点对应的数是多少吗？

查看试题解析
29. 在一条不完整的数轴上从左到右有点A，B，C，其中AB=2，BC=1，如图所示．设点A，B，C所对应数的和是p．

(1)、若以B为原点，则点A，C所对应的数为、， p的值为；若以C为原点，p 的值为；

(2)、若原点O在图中数轴上点C的右边，且CO=28，求p的值．

查看试题解析
30.

(1)、请你在数轴上表示下列有理数： $- \fr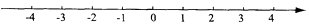ac{1}{2}$ ，— $| - 2.5 |$ ，0，－(－4)．

(2)、将上列各数用“<”号连接起来：

查看试题解析
31. 王先生到市行政中心大楼办事，假定乘电梯向上一楼记作+1，向下一楼记作－1，王先生从1楼出发，电梯上下楼层依次记录如下(单位：层)： +6，－3，+10，－8，+12，－7，－10.

(1)、请你通过计算说明王先生最后是否回到出发点1楼.

(2)、该中心大楼每层高3 m，电梯每向上或下1 m需要耗电0.2度，根据王先生
现在所处位置，请你算算，他办事时电梯需要耗电多少度?

查看试题解析
32. 阅读下面的材料：
如图1，在数轴上A点衰示的数为a，B点表示的数为b，则点A到点B的距离记为AB．线段AB的长可以用右边的数减去左边的数表示，即AB﹣b﹣a．
请用上面的知识解答下面的问题：
如图2，一个点从数轴上的原点开始，先向左移动1cm到达A点，再向左移动2cm到达B点，然后向右移动7cm到达C点，用1个单位长度表示1cm．

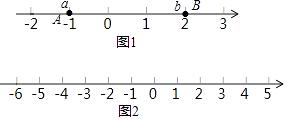(1)、请你在数轴上表示出A．B．C三点的位置：

(2)、点C到点人的距离CA=cm；若数轴上有一点D，且AD=4，则点D表示的数为；

(3)、若将点A向右移动xcm，则移动后的点表示的数为；（用代数式表示）

(4)、若点B以每秒2cm的速度向左移动，同时A．C点分别以每秒1cm、4cm的速度向右移动．设移动时间为t秒，
试探索：CA﹣AB的值是否会随着t的变化而改变？请说明理由．

查看试题解析
33. 如图，半径为1个单位的圆片上有一点A与数轴上的原点重合，
AB是圆片的直径．（注：结果保留π ）

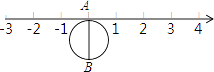(1)、把圆片沿数轴向右滚动半周，点B到达数轴上点C的位置，点C表示的数是数（填“无理”或“有理”），这个数是；

(2)、圆片在数轴上向右滚动的周数记为正数，圆片在数轴上向左滚动的周数记为负数，依次运动情况记录如下：+2，﹣1，+3，﹣4，﹣3
①第次滚动后，A点距离原点最远；
②当圆片结束运动时，此时点A所表示的数是．

查看试题解析
34. 学校图书馆上周借书记录如表（超过50册的部分记为正，少于50册的部分记为负）：
星期一
星期二
星期三
星期四
星期五
0
+8
a
b
﹣7

(1)、上星期五借出图书多少册？

(2)、上周平均每天借出图书为54册，问星期三最多借出多少册图书？

查看试题解析
35. 如图一根木棒放在数轴上，木棒的左端与数轴上的点A重合，右端与点B重合．

(1)、若将木棒沿数轴向右水平移动，则当它的左端移动到B点时，它的右端在数轴上所对应的数为20；若将木棒沿数轴向左水平移动，则当它的右端移动到A点时，则它的左端在数轴上所对应的数为5（单位：cm），由此可得到木棒长为 cm．

(2)、由题（1）的启发，请你能借助“数轴”这个工具帮助小红解决下列问题：
问题：一天，小红去问曾当过数学老师现在退休在家的爷爷的年龄，爷爷说：“我若是你现在这么大，你还要40年才出生；你若是我现在这么大，我已经125岁，是老寿星了，哈哈！”，请求出爷爷现在多少岁了？

查看试题解析
36. 某高速公路养护小组，乘车沿东西向公路巡视维护，如果约定向东为正，向西为负，当天的行驶记录如下（单位：千米）：
﹣8，+18，+2，﹣16，+11，﹣5．

(1)、该养护小组最后到达的地方在出发点的哪个方向？距出发点多远？

(2)、若汽车耗油量为0.5L/km，则这次养护共耗油多少升？

查看试题解析
37. 现有20筐葡萄，以每筐15千克为标准，超过或不足的千克数分别用正、负数来表示，与标准质量的差值记录如下：
单位（千克）
﹣3
﹣2
﹣1.5
0
1
2.5
筐数
1
5
2
2
4

(1)、这20筐葡萄中，最重的一筐比最轻的一筐重千克．

(2)、与标准重量比较，这20筐葡萄总计超过或不足多少千克？

(3)、若葡萄每千克售价8元，则出售这20筐葡萄可卖多少元？

查看试题解析
38. 已知，如图A、B分别为数轴上的两点，A点对应的数为﹣10，B点对应的数为90．

(1)、请写出与AB两点距离相等的M点对应的数；

(2)、现在有一只电子蚂蚁P从B点出发时，以5个单位/秒的速度向左运动，同时另一只电子蚂蚁Q恰好从A点出发，以3个单位/秒的速度向右运动，设两只电子蚂蚁在数轴上的C点相遇，你知道对应的数是多少吗？

(3)、若当电子蚂蚁P从B点出发时，以5个单位/秒的速度向左运动，同时另一只电子蚂蚁Q恰好从A点出发，以3个单位/秒的速度向左运动，经过多长的时间两只电子蚂蚁在数轴上相距30个单位长度？

查看试题解析
39. 在数轴上，已知在纸面上有一数轴（如图），折叠纸面．

(1)、若1表示的点与﹣1表示的点重合，则﹣2表示的点与数表示的点重合；

(2)、若﹣1表示的点与3表示的点重合，5表示的点与数表示的点重合；

(3)、若数轴上A、B两点之间的距离为c个单位长度，点A表示的有理数是a，并且A、B两点经折叠后重合，请写出此时折线与数轴的交点表示的有理数是多少？

查看试题解析
40. 某食品厂从生产的袋装食品中抽出样品20袋，检测每袋的质量是否符合标准，超过或不足的部分分别用正、负数来表示，记录如表：
与标准质量的差值
（单位：g）
﹣5
﹣2
0
1
3
6
袋数
1
4
3
4
5
3

(1)、若标准质量为450克，则抽样检测的20袋食品的平均质量比标准质量多还是少？多或少几克？

(2)、抽样检测的20袋食品的总质量是多少？

(3)、若该种食品的合格标准为450±5g，求该食品的抽样检测的合格率．

查看试题解析

与标准质量的偏差(kg)	﹣1.5	﹣1	﹣0.5	0	0.5	1	2
袋数(袋)	40	30	10	25	40	20	35

城市	悉尼	纽约
时差/时	+2	﹣12

星期一	星期二	星期三	星期四	星期五
0	+8	a	b	﹣7

单位（千克）	﹣3	﹣2	﹣1.5	0	1	2.5
筐数	1	5	2	2	4