初中数学苏科版九年级下册第五章二次函数综合测试卷

试卷更新日期：2021-06-22 类型：单元试卷

进入出卷网下载

一、单选题

1. 将二次函数y=(x﹣1)²+2的图象向上平移3个单位长度，得到的拋物线相应的函数表达式为（）

A、y=(x+2)²﹣2 B、y=(x﹣4)²+2 C、y=(x﹣1)²﹣1 D、y=(x﹣1)²+5

查看试题解析
2. 已知学校航模组设计制作的火箭的升空高度h（m）与飞行时间t（s）满足函数表达式h＝﹣t²＋24t＋1．则下列说法中正确的是（）

A、点火后9s和点火后13s的升空高度相同 B、点火后24s火箭落于地面 C、点火后10s的升空高度为139m D、火箭升空的最大高度为145m

查看试题解析
3. 将抛物线y=x²向右平移2个单位，再向上平移1个单位，所得抛物线相应的函数表达式是（）

A、y=（x+2）²+1 B、y=（x+2）²﹣1 C、y=（x﹣2）²+1 D、y=（x﹣2）²﹣1

查看试题解析
4. 若函数y=x²﹣2x+b的图象与坐标轴有三个交点，则b的取值范围是（）

A、b＜1且b≠0 B、b＞1 C、0＜b＜1 D、b＜1

查看试题解析
5. 点P(m，n)在以y轴为对称轴的二次函数y＝x²+ax+4的图象上.则m﹣n的最大值等于（）

A、 $\frac{15}{4}$ B、4 C、﹣ $\frac{15}{4}$ D、﹣ $\frac{17}{4}$

查看试题解析
6. 如图是王阿姨晚饭后步行的路程s(单位：m)与时间t(单位：min)的函数图象，其中曲线段AB是以B为顶点的抛物线一部分.下列说法不正确的是（）

A、25min~50min，王阿姨步行的路程为800m B、线段CD的函数解析式为 $s = 32 t + 400 （ 25 \leq t \leq 50 ）$ C、5min~20min，王阿姨步行速度由慢到快 D、曲线段AB的函数解析式为 $s = - 3 （ t - 20 ）^{2} + 1200 （ 5 \leq t \leq 20 ）$

查看试题解析
7. 如图，已知△ABC的顶点坐标分别为A（0，2）、B（1，0）、C（2，1），若二次函数y=x²+bx+1的图象与阴影部分（含边界）一定有公共点，则实数b的取值范围是（）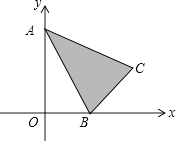

A、b≤﹣2 B、b＜﹣2 C、b≥﹣2 D、b＞﹣2

查看试题解析
8. 已知抛物线y=ax²（a＞0）过A（﹣2，y₁）、B（1，y₂）两点，则下列关系式一定正确的是（）

A、y₁＞0＞y₂ B、y₂＞0＞y₁ C、y₁＞y₂＞0 D、y₂＞y₁＞0

查看试题解析
9. 如图，在Rt△ABC中，∠C=90°，AC=6cm，BC=2cm，点P在边AC上，从点A向点C移动，点Q在边CB上，从点C向点B移动．若点P，Q均以1cm/s的速度同时出发，且当一点移动到终点时，另一点也随之停止，连接PQ，则线段PQ的最小值是（）

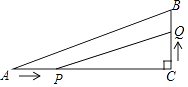A、20cm B、18cm C、2 $\sqrt{5}$ cm D、3 $\sqrt{2}$ cm

查看试题解析
10. 如图，将函数y= $\frac{1}{2}$ （x﹣2）²+1的图象沿y轴向上平移得到一条新函数的图象，其中点A（1，m），B（4，n）平移后的对应点分别为点A'、B'．若曲线段AB扫过的面积为9（图中的阴影部分），则新图象的函数表达式是（）

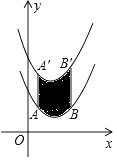A、 $y = \frac{1}{2} {(x - 2)}^{2} - 2$ B、 $y = \frac{1}{2} {(x - 2)}^{2} + 7$ C、 $y = \frac{1}{2} {(x - 2)}^{2} - 5$ D、 $y = \frac{1}{2} {(x - 2)}^{2} + 4$

查看试题解析
11.
如图，已知抛物线 $y_{1} = - x^{2} + 4 x$ 和直线 $y_{2} = 2 x$ .我们约定：当x任取一值时，x对应的函数值分别为y₁、y₂ ，若y₁≠y₂ ，取y₁、y₂中的较小值记为M；若y₁=y₂ ，记M= y₁=y₂.
下列判断： ①当x＞2时，M=y₂；
②当x＜0时，x值越大，M值越大；
③使得M大于4的x值不存在；
④若M=2，则x=1.
其中正确的有

A、1个 B、2个 C、3个 D、4个

查看试题解析
12. 如图，矩形ABCD中，AB=8，AD=4，E为边AD上一个动点，连接BE，取BE的中点G，点G绕点E逆时针旋转90°得到点F，连接CF，则△CEF面积的最小值是（）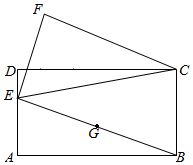

A、16 B、15 C、12 D、11

查看试题解析

二、填空题

13. 下列关于二次函数 $y = - {(x - m)}^{2} + m^{2} + 1$ （ $m$ 为常数）的结论，①该函数的图象与函数 $y = - x^{2}$ 的图象形状相同；②该函数的图象一定经过点 $(0 ， 1)$ ；③当 $x > 0$ 时，y随x的增大而减小；④该函数的图象的顶点在函数 $y = x^{2} + 1$ 的图像上，其中所有正确的结论序号是.

查看试题解析
14. 已知二次函数的图象经过点 $P (2 ， 2)$ ，顶点为 $O (0 ， 0)$ 将该图象向右平移，当它再次经过点 $P$ 时，所得抛物线的函数表达式为.

查看试题解析
15. 已知抛物线 $y = a x^{2} + 4 a x + 4 a + 1 (a \neq 0)$ 过点 $A (m ， 3)$ ， $B (n ， 3)$ 两点，若线段 $A B$ 的长不大于 $4$ ，则代数式 $a^{2} + a + 1$ 的最小值是.

查看试题解析
16. 某个函数具有性质：当 $x$ >0时， $y$ 随 $x$ 的增大而增大，这个函数的表达式可以是（只要写出一个符合题意的答案即可）

查看试题解析
17. 将二次函数 $y = x^{2} - 1$ 的图像向上平移3个单位长度，得到的图像所对应的函数表达式是．

查看试题解析
18. 已知抛物线y=ax²+bx+c与x轴的公共点是（﹣4，0），（2，0），则这条抛物线的对称轴是直线．

查看试题解析
19. 已知二次函数y=ax²+bx+c中，函数y与自变量x的部分对应值如表：
x
…
﹣1
0
1
2
3
…
y
…
10
5
2
1
2
…
则当y＜5时，x的取值范围是．

查看试题解析
20. 将二次函数y=2x²﹣1的图象沿y轴向上平移2个单位，所得图象对应的函数表达式为．

查看试题解析
21. 若函数y=mx²+2x+1的图象与x轴只有一个公共点，则常数m的值是．

查看试题解析
22. 如图，已知函数y= $- \frac{3}{x}$ 与y=ax²+bx（a＞0，b＞0）的图象交于点P．点P的纵坐标为1．则关于x的方程ax²+bx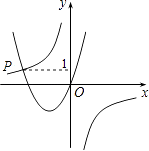+ $\frac{3}{x}$ =0的解为．

查看试题解析
23. 在平面直角坐标系xOy中，抛物线y = x² – 2 m x – 2m – 2与直线y =-x-2 交于C，D两点，将抛物线在C、D两点之间的部分(不含C、D）上恰有两个点的横坐标为整数，则m的取值范围为.

查看试题解析
24. 如图，矩形ABCD中，AB＝6，BC＝8，E为AB的中点，P为BC上一动点，作PQ⊥EP交直线CD于点Q，设点P每秒以1个单位长度的速度从点B运动到点C停止，在此时间段内，点Q运动的平均速度为每秒个单位.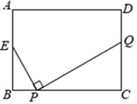

查看试题解析

三、解答题

25.
如图，二次函数 $y = x^{2} + b x + c$ 的图像与 $x$ 轴交于 $Α$ 、 $Β$ 两点，与 $y$ 轴交于点 $C$ ， $Ο Β = Ο C$ ．点 $D$ 在函数图象上， $CD// x$ 轴，且 $CD = 2$ ，直线 $l$ 是抛物线的对称轴， $Ε$ 是抛物线的顶点．
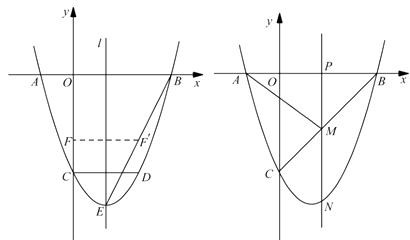
图 ① 图②

(1)、求 $b$ 、 $c$ 的值；

(2)、如图①，连接 $Β Ε$ ，线段 $Ο C$ 上的点 $F$ 关于直线 $l$ 的对称点 $F^{'}$ 恰好在线段 $Β Ε$ 上，求点 $F$ 的坐标；

(3)、如图②，动点 $Ρ$ 在线段 $Ο Β$ 上，过点 $Ρ$ 作 $x$ 轴的垂线分别与 $Β C$ 交于点 $Μ$ ，与抛物线交于点 $Ν$ ．试问：抛物线上是否存在点 $Q$ ，使得 $Δ Ρ Q Ν$ 与 $Δ Α Ρ Μ$ 的面积相等，且线段 $Ν Q$ 的长度最小？如果存在，求出点 $Q$ 的坐标；如果不存在，说明理由．

查看试题解析
26.
阅读材料：如图1，在平面直角坐标系中，A、B两点的坐标分别为A（x₁ ， y₁），B（x₂ ， y₂），AB中点P的坐标为（x_p ， y_p）．由x_p﹣x₁=x₂﹣x_p ，得x_p= $\frac{x_{1} + x_{2}}{2}$ ，同理y_p= $\frac{y_{1} + y_{2}}{2}$ ，所以AB的中点坐标为（ $\frac{x_{1} + x_{2}}{2}$ ， $\frac{y_{1} + y_{2}}{2}$ ）．由勾股定理得AB²=|x₂﹣x₁|₂+|y₂﹣y₁|² ，所以A、B两点间的距离公式为AB= $\sqrt{{(x_{2} - x_{1})}^{2} + {(y_{2} - y_{1})}^{2}}$ ．这两公式对A、B在平面直角坐标系中其它位置也成立．解答下列问题：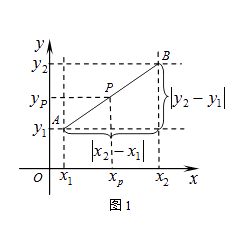

(1)、已知M（1，﹣2），N（﹣1，2），直接利用公式填空：MN中点坐标为， MN= ．

(2)、
如图2，直线l：y=2x+2与抛物线y=2x²交于A、B两点，P为AB的中点，过P作x轴的垂线交抛物线于点C．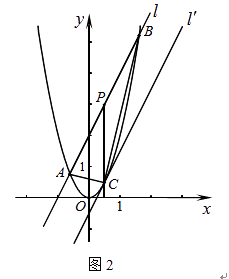
（a）求A、B两点的坐标及C点的坐标；
（b）连结AB、AC，求证△ABC为直角三角形；
（c）将直线l平移到C点时得到直线l′，求两直线l与l′的距离．

查看试题解析
27.
如图，已知抛物线 $y = - \frac{1}{2} (x + 1) (x - b)$ （其中 $b > 1$ ）与x轴交于点A、B（点A在点B的左侧），与y轴交于点C，抛物线的对称轴l与x轴交于点D，且点D恰好在线段BC的垂直平分线上．

(1)、求抛物线的关系式；

(2)、过点 $M (1 ， 0)$ 的线段MN∥y轴，与BC交于点P，与抛物线交于点N．若点E是直线l上一点，且∠BED＝∠MNB－∠ACO时，求点E的坐标．

查看试题解析
28.
已知抛物线 $y = x^{2} - 2 x - 3$

(1)、此抛物线的顶点坐标是，与x轴的交点坐标是，，与y轴交点坐标是，对称轴直线是；

(2)、在平面直角坐标系中画出 $y = x^{2} - 2 x - 3$ 的图象；

(3)、结合图象，说明当x取何值时，y随x的增大而减小．

查看试题解析
29.
如图，已知抛物线y=ax²+bx+1经过点（2，6），且与直线 $y = \frac{1}{2} x + 1$ 相交于A，B两点，点A在y轴上，过点B作BC⊥x轴，垂足为点C（4，0）．

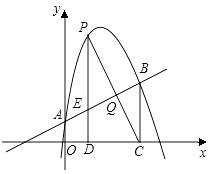(1)、求抛物线的解析式；

(2)、若P是直线AB上方该抛物线上的一个动点，过点P作PD⊥x轴于点D，交AB于点E，求线段PE的最大值；

(3)、在（2）的条件，设PC与AB相交于点Q，当线段PC与BE相互平分时，请求出点Q的坐标．

查看试题解析
30. 旅游公司在景区内配置了50辆观光车供游客租赁使用，假定每辆观光车一天内最多只能出租一次，且每辆车的日租金是x（元）．发现每天的营运规律如下：当x不超过100元时，观光车能全部租出；当x超过100元时，每辆车的日租金每增加5元，租出去的观光车就会减少1辆．已知所有观光车每天的管理费是1100元．当每辆车的日租金为多少元时，每天的净收入最多？（注：净收入=租车收入﹣管理费）

查看试题解析

四、综合题

31. 已知二次函数 $y = - x^{2} + 2 m x - m^{2} - m + 2$ （ $m$ 是常数）.

(1)、若该函数图象与 $x$ 轴有两个不同的公共点，求 $m$ 的取值范围；

(2)、求证：不论 $m$ 为何值，该函数图象的顶点都在函数 $y = - x + 2$ 的图象上；

(3)、 $P (x_{1} ， y_{1})$ ， $Q (x_{2} ， y_{2})$ 是该二次函数图象上的点，当 $1 < x_{1} < x_{2}$ 时，都有 $y_{2} < y_{1} < 1$ ，则 $m$ 的取值范围是.

查看试题解析
32. 已经二次函数 $y = a x^{2} + b x + 1$ .

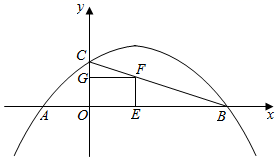(1)、如图，其图象与x轴交于点 $A (- 1 ， 0)$ 和点B，与y轴交于点C，对称轴为直线 $x = 1$ .
①求二次函数解析式；

②F为线段BC上一点，过F分别作x轴，y轴垂线，垂足分别为E、F，当四边形 $O E F G$ 为正方形时，求点F坐标；

(2)、其图象上仅有一个点的横坐标、纵坐标互为相反数，且二次函数 $y = a x^{2} + b x + 1$ 函数值存在负数，求b的取值范围.

查看试题解析
33. 专卖店卖某品牌文化衫，如果每件利润为30元（市场管理部门规定，该品牌文化衫每件利润不能超过50元），每天可售出50件.根据市场调查发现，销售单价每增加2元，每天销售量会减少1件.设销售单价增加x元，每天售出y件.

(1)、请写出y与x之间的函数表达式；（写出自变量x的范围）

(2)、当x为多少时，超市每天销售这种品牌文化衫可获利润1932元？

(3)、设超市每天销售这种文化衫可获利w元，当x为多少时w最大，最大值是多少？

查看试题解析
34. 城市内环高架能改善整个城市的交通状况.在一般情况下，高架上的车流速度 $v$ （单位：千米/小时）是车流密度 $x$ （单位：辆/千米）的函数.当高架上的车流密度达到188辆/千米时，造成堵塞，此时车流速度为0；当车流密度不超过28辆/千米时，车流速度为80千米/小时.研究表明：当 $28 \leq x \leq 188$ 时，车流速度 $v$ 是车流密度 $x$ 的一次函数.

(1)、当 $28 \leq x \leq 188$ 时，求车流速度 $v$ 关于车流密度 $x$ 的函数解析式；

(2)、若车流速度 $v$ 不低于50千米/小时，求车流密度 $x$ 为多大时，车流量 $y$ （单位时间内通过高架桥上某观测点的车辆数，单位：辆/小时）可以达到最大，并求出最大值.

查看试题解析
35. 如图，抛物线y＝x²+bx+c与x轴交于A、B两点，与y轴交于点C，OA＝OC＝3，顶点为点D.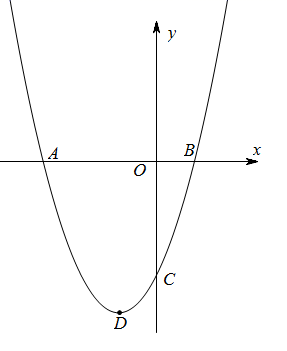

(1)、求此抛物线的函数表达式；

(2)、判断△ACD的形状，并说明理由.

查看试题解析
36. 为积极响应国家“旧房改造”工程，该市推出《加快推进旧房改造工作的实施方案》推进新型城镇化建设，改善民生，优化城市建设.

(1)、根据方案该市的旧房改造户数从2020年底的3万户增长到2022年底的4.32万户，求该市这两年旧房改造户数的平均年增长率；

(2)、该市计划对某小区进行旧房改造，如果计划改造300户，计划投入改造费用平均20000元/户，且计划改造的户数每增加1户，投入改造费平均减少50元/户，求旧房改造申报的最高投入费用是多少元？

查看试题解析
37. 已知：二次函数C₁：y₁＝ax²+2ax+a-1（a≠0）.

(1)、把二次函数C₁的表达式化成y＝a（x-h）²+b（a≠0）的形式，并写出顶点坐标；

(2)、已知二次函数C₁的图象经过点A(-3，1).
①a的值；

②点B在二次函数C₁的图象上，点A，B关于对称轴对称，连接AB.二次函数C₂：y₂＝kx²+kx（k≠0）的图象，与线段AB只有一个交点，则k的取值范围.

查看试题解析
38. 某公司经过市场调查，发现某种运动服的销量与售价是一次函数关系，具体信息如表：

已知该运动服的进价为每件150元.

(1)、售价为x元，月销量为y件.
①求y关于x的函数关系式：

②若销售该运动服的月利润为w元，求w关于x的函数关系式，并求月利润最大时的售价；

(2)、由于运动服进价降低了a元，商家决定回馈顾客，打折销售，这时月销量与调整后的售价仍满足（1）中函数关系式.结果发现，此时月利润最大时的售价比调整前月利润最大时的售价低15元，则a的值是多少？

查看试题解析
39. 为了节省材料，某水产养殖户利用水库的岸堤（岸堤足够长）为一边，用总长为 $80$ 米的围网在水库中围成了如图所示的①②③三块矩形区域，而且这三块矩形区域的面积相等.设 $B C$ 的长度为 $x$ 米，矩形区域 $A B C D$ 的面积为 $y$ 米 $^{2}$ .

(1)、求证： $A E = 2 B E$ ；

(2)、求y与x之间的函数关系式，并写出自变量x的取值范围；

(3)、x为何值时，y有最大值？最大值是多少？

查看试题解析
40. 在平面直角坐标系xOy中，已知抛物线y＝x²﹣mx+n.

(1)、当m＝2时，
①求抛物线的对称轴，并用含n的式子表示顶点的纵坐标；

②若点A（﹣2，y₁），B（x₂ ， y₂）都在抛物线上，且y₂＞y₁ ，求x₂的取值范围；

(2)、已知点P（﹣1，2），将点P向右平移4个单位长度，得到点Q.当n＝3时，若抛物线与线段PQ恰有一个公共点，结合函数图象，求m的取值范围.

查看试题解析

x	…	﹣1	0	1	2	3	…
y	…	10	5	2	1	2	…

初中数学苏科版九年级下册第五章二次函数 综合测试卷

一、单选题

二、填空题

三、解答题

四、综合题

初中数学苏科版九年级下册第五章二次函数综合测试卷