初中数学苏科版九年级下册5.5 用二次函数解决问题 同步练习
试卷更新日期：2021-06-22 类型：同步测试
一、单选题
-
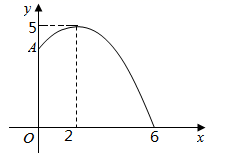
1. 从地面竖直向上抛出一小球，小球的高度h（单位：m）与小球运动时间t（单位：s）之间的函数关系如图所示.下列结论：①小球抛出3秒时达到最高点；②小球从抛出到落地经过的路程是80m；③小球的高度h＝20时，t＝1s或5s.④小球抛出2秒后的高度是35m.其中正确的有（ ）
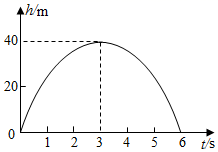A、①② B、②③ C、①③④ D、①②③2. 图(1)是一个横断面为抛物线形状的拱桥，当水面在L时，拱顶(拱桥洞的最高点)离水面2m，水面宽为4m.如果水面宽度为6m，则水面下降 （ ）
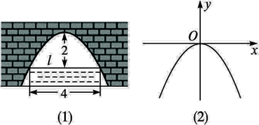A、3.5 B、3 C、2.5 D、23. 竖直向上的小球离地面的高度h（米）与时间t（秒）的关系函数关系式为h=-2t2+mt+ ，若小球经过 秒落地，则小球在上抛过程中，第（ ）秒离地面最高.A、 B、 C、 D、4. 如图，已知二次函数y=mx2-4mx+3m(m>0)的图像与x轴交于A，B两点，与y轴交于点C，连接AC、BC，若CA平分∠OCB，则m的值为（ ）
A、 B、 C、 D、5. 如图，利用一个直角墙角修建一个梯形储料场ABCD，其中∠C＝120°.若新建墙BC与CD总长为12m，则该梯形储料场ABCD的最大面积是（ ）
A、18m2 B、 m2 C、 m2 D、 m26. 若 表示 三个数中的最小值，当 时 ，则 的最大值是（ ）A、4 B、5 C、6 D、77. 如图，二次函数 的最大值为3，一元二次方程 有实数根，则 的取值范围是（ ）
A、m≥3 B、m≥-3 C、m≤3 D、m≤-38. 如图，⊙O是以原点为圆心， 为半径的圆，点 是直线 上的一点，过点 作⊙O的一条切线PQ，Q为切点，则切线长PQ的最小值为（ ）
A、3 B、4 C、
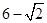D、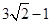
9. 一种包装盒的设计方法如图所示，ABCD是边长为80cm的正方形硬纸片，切去阴影部分所示的四个全等的等腰直角三角形，再沿虚线折起，使得A，B，C，D四点重合于图中的点O，形成一个底面为正方形的长方体包装盒，设BE＝CF＝xcm，要使包装盒的侧面积最大，则x应取（ ）
A、30cm B、25cm C、20cm D、15cm10. 为搞好环保，某公司准备修建一个长方体的污水处理池，池底矩形的周长为100m，则池底的最大面积是（ ）A、600 m2 B、625 m2 C、650 m2 D、675 m2二、填空题
-
11. 如图，要修建一个圆形喷水池，在池中心竖直安装一根水管，在水管的顶端A点安一个喷水头，使喷出的抛物线形水柱在与池中心的水平距离为 处达到最高，高度为 ，水柱落地处离池中心距离为 ，则水管的长度 是 .
12. 王翔同学在一次跳高训练中采用了背跃式，跳跃路线正好和抛物线 相吻合，那么他能跳过的最大高度为m.13. 道路的隔离栏通常会涂上醒目的颜色，呈抛物线形状（如图 ），图 是一个长为 米，宽为 米的矩形隔离栏，中间被 根栏杆五等分，每根栏杆的下面一部分涂上醒目的蓝色，颜色的分界处（点 ，点 ）以及点 ，点 落在同一条抛物线上，若第 根栏杆涂色部分（ ）与第 根栏杆未涂色部分（ ）长度相等，则 的长度是.
14. 定义：对角线互相垂直的四边形为垂美四边形.已知垂美四边形ABCD的对角线AC、BD满足AC＋BD＝12，则当AC＝时，四边形ABCD的面积最大.15. 如图，某大桥有一段抛物线形的拱梁，抛物线的解析式为y＝ax2＋bx，小强骑自行车从拱梁一端O匀速穿过拱梁部分的桥面OC，当小强骑自行车行驶到6分钟和14分钟时拱梁的高度相同，则小强骑自行车通过拱梁部分的桥面OC共需分钟.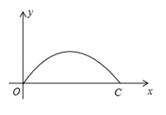
16. 某大学的校门如图所示是抛物线形水泥建筑物，大门内侧的地面宽度为8米，两侧距地面4米高处各有一个挂校名横匾用的铁环，两铁环的水平距离为6米，那么校门内侧距地面的高是米.
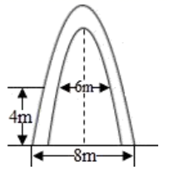17. 已知，四边形ABCD的两条对角线AC、BD互相垂直，且AC+BD＝10，当AC＝时，四边形ABCD的面积最大，最大值为.18. 将一条长为20 cm的铁丝剪成两段并用每一段铁丝刚好围成一个正方形，则这两个正方形面积之和的最小值是 .19. 加工爆米花时，爆开且不糊的颗粒的百分比称为“可食用率”.在特定条件下，可食用率 与加工时间 （单位： ）满足函数表达式 ，则最佳加工时间为 .20. 用一根长为20cm的铁丝围成一个矩形，那么这个矩形的面积可能是cm2(写出1个可能的值即可)三、解答题
-
21. 某汽车出租公司以每辆汽车月租费3000元，100辆汽车可以全部租出.若每辆汽车的月租费每增加50元，则将少租1辆汽车.已知每辆租出的汽车支付月维护费200元，问每月租出多少辆汽车时，该出租公司的月收益最大？最大月收益是多少？22. 如图所示，公园要造圆形的喷水池，在水池中央垂直于水面处安装一个柱子OA，O恰在水面中心，OA=1.25m，由柱子顶端A处的喷头向外喷水，水流在各个方向沿形状相同的抛物线路线落下，为使水流形状较为漂亮，要求设计成水流在离OA距离为1m处达到距水面距离最大，高度2.25m.若不计其他因素，那么水池的半径至少要多少米才能使喷出的水流不致落到池外?
23. 某商场将进价40元一个的某种商品按50元一个售出时，每月能卖出500个.商场想了两个方案来增加利润：方案一：提高价格，但这种商品每个售价涨价1元，销售量就减少10个；
方案二：售价不变，但发资料做广告.已知当这种商品每月的广告费用为m(千元)时，每月销售量将是原销售量的p倍，且p =
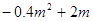.试通过计算，请你判断商场为赚得更大的利润应选择哪种方案？请说明你判断的理由！
24. 知识迁移当a＞0且x＞0时，因为 ，所以x﹣ + ≥0，从而x+ ≥ （当x= ）是取等号）．
记函数y=x+ （a＞0，x＞0）．由上述结论可知：当x= 时，该函数有最小值为2 ．
直接应用
已知函数y1=x（x＞0）与函数y2= （x＞0），则当x=1时，y1+y2取得最小值为2．
变形应用
已知函数y1=x+1（x＞﹣1）与函数y2=（x+1）2+4（x＞﹣1），求 的最小值，并指出取得该最小值时相应的x的值．
实际应用
已知某汽车的一次运输成本包含以下三个部分，一是固定费用，共360元；二是燃油费，每千米1.6元；三是折旧费，它与路程的平方成正比，比例系数为0.001．设该汽车一次运输的路程为x千米，求当x为多少时，该汽车平均每千米的运输成本最低？最低是多少元？
25. 某商场购进一批L型服装（数量足够多），进价为40元/件，以60元/件销售，每天销售20件，根据市场调研，若每件降价1元，则每天销售数量比原来多3件．现商场决定对L型服装开展降价促销活动，每件降价x元（x为正整数）．在促销期间，商场要想每天获得最大销售毛利润，每件应降价多少元？每天最大销售毛利润为多少？（注：每件服装销售毛利润是指每件服装的销售价与进货价的差）26. 某涵洞的截面边缘成抛物线形，现测得当水面宽AB=2米时涵洞的顶点与水面的距离为4米，这时离开水面2米处涵洞宽DE是多少？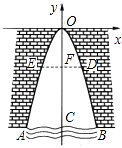
27. 公司投资750万元，成功研制出一种市场需求量较大的产品，并再投入资金1750万元进行相关生产设备的改进．已知生产过程中，每件产品的成本为60元．在销售过程中发现，当销售单价定为120元时，年销售量为24万件；销售单价每增加10元，年销售量将减少1万件．设销售单价为x（元）（x＞120），年销售量为y（万件），第一年年获利（年获利=年销售额﹣生产成本）为z（万元）．（1）求出y与x之间，z与x之间的函数关系式；
（2）该公司能否在第一年收回投资．
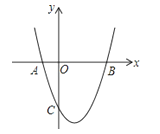
28.如图，抛物线y=ax2+bx+c与x轴交于A（﹣1，0），B（3，0）两点，与y轴交于C（0，﹣3）．
（1）求抛物线的解析式；
（2）D是y轴正半轴上的点，OD=3，在线段BD上任取一点E（不与B，D重合），经过A，B，E三点的圆交直线BC于点F，
①试说明EF是圆的直径；
②判断△AEF的形状，并说明理由．
29. 今年以来，国务院连续发布了《关于加快构建大众创业万众创新支撑平台的指导意见》等一系列支持性政策，各地政府高度重视、积极响应，中国掀起了大众创业万众创新的新浪潮．某创新公司生产营销A、B两种新产品，根据市场调研，发现如下信息：信息1：销售A种产品所获利润y（万元）与所售产品x（吨）之间存在二次函数关系y=ax2+bx，当x=1时，y=7；当x=2时，y=12．
信息2：销售B种产品所获利润y（万元）与所售产品x（吨）之间存在正比例函数关系y=2x．
根据以上信息，解答下列问题：
（1）求a，b的值；
（2）该公司准备生产营销A、B两种产品共10吨，请设计一个生产方案，使销售A、B两种产品获得的利润之和最大，最大利润是多少？
30. 汽车租赁行业现在火爆起来．小明开办了一家汽车租赁公司，拥有汽车20辆，在旺季每辆车的每天租金为600元时，可全部租出：当每辆车的每天租金增加50元时，未租出的车将增加一辆，租出的车辆每辆每天需要维护费200元，未租出的车辆每辆每天需要维护费100元，每天其他开销共计1000元．（1）当每辆车的租金为1000元时，每天能租出多少辆车？每天净收益为多少元？
（2）当每辆车的每天租金定为多少元时，租赁公司的每天净收益最大？最大净收益为多少元？（每天净收益=总租金﹣租出去车辆维护费﹣未租出去车辆维护费﹣每天其他开销）
四、综合题
-
31. 某商场经营某种品牌的玩具，购进时的单价是40元，根据市场调查：在一段时间内，销售单价是50元时，销售量是600件，而销售单价每涨2元，就会少售出20件玩具.(1)、不妨设该种品牌玩具的销售单价为x元（x＞50），请你分别用x的代数式来表示销售量y件和销售该品牌玩具获得利润ω元，并把结果填写在表格中：
销售单价（元）
x
销售量y（件）
销售玩具获得利润ω（元）
(2)、在（1）问条件下，若玩具厂规定该品牌玩具销售单价不低于54元，且商场要完成不少于400件的销售任务，求商场销售该品牌玩具获得的最大利润是多少元？32. 某水果销售店在草莓销售旺季，试销售成本为每千克20元的草莓，规定试销期间销售单价不低于成本单价，也不高于每千克40元，经试销发现，销售量y（千克）与销售单价x（元）符合一次函数关系，如图是y与x的函数关系图象.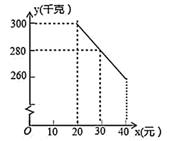
(1)、求y与x的函数解析式；(2)、设该水果销售店试销草莓获得的利润为W元，求W的最大值.33. 某超市销售一种时尚玩具，进价为每件10元，售价为每件12元时，当天的销售量为200件，在销售过程中发现：售价每上涨0.5元，当天的销售量就减少10件.设当天销售单价统一为每件x元（ ，且是按着0.5元的倍数上涨），当天销售利润为y元.(1)、求y与x的函数关系式（不要求写出自变量的取值范围）；(2)、若当天销售利润为640元，求当天的销售单价；(3)、若每件玩具的利润不超过80%，要想当天获得利润最大，每件玩具的售价应为多少元？并求出最大利润.34. 某商店经过市场调查，整理出某种商品在第x(1≤x≤90)天的售价与销量的相关信息如下表：时间x(天)
1≤x＜50
50≤x≤90
售价(元/件)
x＋40
90
每天销量(件)
200－2x
已知该商品的进价为每件30元，设销售该商品的每天利润为y元.
(1)、求出y与x的函数关系式；(2)、问销售该商品第几天时，当天销售利润最大，最大利润是多少？35. 某商场销售一种小商品，进货价为8元/件.当售价为10元/件时，每天的销售量为100件.在销售过程中发现：销售单价每上涨0.1元，每天的销售量就减少1件.设销售单价为x元/件（ ），每天销售利润为y元.(1)、求y与x的函数关系式；(2)、要使每天销售利润不低于270元，求销售单价所在的范围；(3)、若每件该小商品的利润不超过 ，则每件该小商品的销售单价定为多少元时，每天获得的利润最大.最大利润是多少？36. 某公司生产的商品的市场指导价为每件500元，公司的实际销售价格可以浮动x个百分点，即销售价格=500（1+x%），经过市场调研发现，这种商品的日销售量y（件）与销售价格浮动的百分点x之间的函数关系为y=-10x+120，若该公司按浮动-12个百分点的价格出售，每件商品仍可获利10%.(1)、求该公司生产销售每件商品的成本为多少元；(2)、当该公司的商品定价为每件多少元时，日销售利润最多？最多是多少元？（说明：日销售利润=（销售价格-成本）×日销售量）(3)、该公司决定每销售一件商品就捐赠m元利润（m≥l）给希望工程，公司通过销售记录发现，当价格浮动的百分点大于-3时，扣除捐赠后的日销售利润随x增大而减小，直接写出m的取值范围.37. 如图，在一次高尔夫球的比赛中，某运动员在原点O处击球，目标是离击球点10米远的球洞，球的飞行路线是一条抛物线，结果球的落地点距离球洞2米，（击球点、落地点、球洞三点共线）球在空中最高处达3.2米.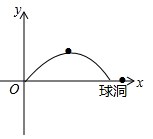
(1)、求表示球飞行的高度y（单位：米）与表示球飞出的水平距离x（单位：米）之间的函数关系式；(2)、当球的飞行高度不低于3米时，求x的取值范围.38. 如图，隧道的截面由抛物线 和矩形 构成，矩形的长 为 ，宽 为 ，隧道最高点E距离地面 ，以 所在的直线为x轴，线段 的垂直平分线为y轴，建立平面直角坐标系，y轴是抛物线的对称轴.
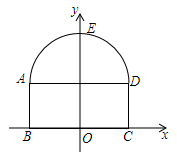(1)、求该抛物线的关系式；(2)、现有一辆货运卡车高 ，宽 ，这辆货运卡车能否通过该隧道？通过计算说明你的结论.39. 传统节日“春节”到来之际，某商店老板以每件60元的价格购进一批商品，若以单价80元销售，每月可售出300件.调查表明：单价每上涨1元，该商品每月的销售量就减少10件.(1)、请写出每月销售该商品的利润y（元）与单价x（元）间的函数关系式；(2)、单价定为多少元时，每月销售商品的利润最大？最大利润为多少？40. 如图，二次函数的图象与x轴相交于A(−3，0)、B(1，0)两点，与y轴相交于点C(0，3)，点C.D是二次函数图象上的一对对称点，一次函数的图象过点B，D.
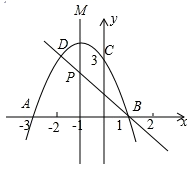(1)、D点坐标；(2)、求二次函数的解析式；(3)、根据图象直接写出使一次函数值小于二次函数值的x的取值范围；