浙江省温州市2021年中考数学试卷
试卷更新日期:2021-06-22 类型:中考真卷
一、选择题(本题有10小题,每小题4分,共40分.每小题只有一个选项是正确的,不选、多选、错选,均不给分)
-
1. 计算 的结果是( )A、4 B、-4 C、1 D、-12. 直六棱柱如图所示,它的俯视图是( )
 A、
A、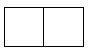 B、
B、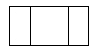 C、
C、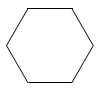 D、
D、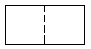 3. 第七次全国人口普查结果显示,我国具有大学文化程度的人口超218000000人.数据218000000用科学记数法表示为( )A、 B、 C、 D、4. 如图是某天参观温州数学名人馆的学生人数统计图.若大学生有60人,则初中生有( )
3. 第七次全国人口普查结果显示,我国具有大学文化程度的人口超218000000人.数据218000000用科学记数法表示为( )A、 B、 C、 D、4. 如图是某天参观温州数学名人馆的学生人数统计图.若大学生有60人,则初中生有( )某天参观温州数学名人馆的学生人数统计图
 A、45人 B、75人 C、120人 D、300人5. 解方程 ,以下去括号正确的是( )A、 B、 C、 D、6. 如图,图形甲与图形乙是位似图形, 是位似中心,位似比为 ,点 , 的对应点分别为点 , .若 ,则 的长为( )
A、45人 B、75人 C、120人 D、300人5. 解方程 ,以下去括号正确的是( )A、 B、 C、 D、6. 如图,图形甲与图形乙是位似图形, 是位似中心,位似比为 ,点 , 的对应点分别为点 , .若 ,则 的长为( )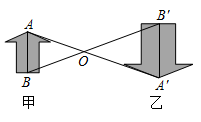 A、8 B、9 C、10 D、157. 某地居民生活用水收费标准:每月用水量不超过17立方米,每立方米 元;超过部分每立方米 元.该地区某用户上月用水量为20立方米,则应缴水费为( )A、 元 B、 元 C、 元 D、 元8. 图1是第七届国际数学教育大会(ICME)的会徽,在其主体图案中选择两个相邻的直角三角形,恰好能组合得到如图2所示的四边形 .若 . ,则 的值为( )
A、8 B、9 C、10 D、157. 某地居民生活用水收费标准:每月用水量不超过17立方米,每立方米 元;超过部分每立方米 元.该地区某用户上月用水量为20立方米,则应缴水费为( )A、 元 B、 元 C、 元 D、 元8. 图1是第七届国际数学教育大会(ICME)的会徽,在其主体图案中选择两个相邻的直角三角形,恰好能组合得到如图2所示的四边形 .若 . ,则 的值为( ) A、 B、 C、 D、9. 如图,点 , 在反比例函数 ( , )的图象上, 轴于点 , 轴于点 , 轴于点 ,连结 .若 , , ,则 的值为( )
A、 B、 C、 D、9. 如图,点 , 在反比例函数 ( , )的图象上, 轴于点 , 轴于点 , 轴于点 ,连结 .若 , , ,则 的值为( )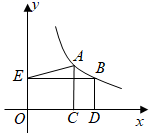 A、2 B、 C、 D、10. 由四个全等的直角三角形和一个小正方形组成的大正方形 如图所示.过点 作 的垂线交小正方形对角线 的延长线于点 ,连结 ,延长 交 于点 .若 ,则 的值为( )
A、2 B、 C、 D、10. 由四个全等的直角三角形和一个小正方形组成的大正方形 如图所示.过点 作 的垂线交小正方形对角线 的延长线于点 ,连结 ,延长 交 于点 .若 ,则 的值为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本题有6小题,每小题5分,共30分)
-
11. 分解因式: .12. 一个不透明的袋中装有21个只有颜色不同的球,其中5个红球,7个白球,9个黄球.从中任意摸出1个球是红球的概率为.13. 若扇形的圆心角为 ,半径为17,则扇形的弧长为.14. 不等式组 的解为.15. 如图, 与 的边 相切,切点为 .将 绕点 按顺时针方向旋转得到 ,使点 落在 上,边 交线段 于点 .若 ,则 度.
 16. 图1是邻边长为2和6的矩形,它由三个小正方形组成,将其剪拼成不重叠、无缝隙的大正方形(如图2),则图1中所标注的 的值为;记图1中小正方形的中心为点 , , ,图2中的对应点为点 , , .以大正方形的中心 为圆心作圆,则当点 , , 在圆内或圆上时,圆的最小面积为.
16. 图1是邻边长为2和6的矩形,它由三个小正方形组成,将其剪拼成不重叠、无缝隙的大正方形(如图2),则图1中所标注的 的值为;记图1中小正方形的中心为点 , , ,图2中的对应点为点 , , .以大正方形的中心 为圆心作圆,则当点 , , 在圆内或圆上时,圆的最小面积为.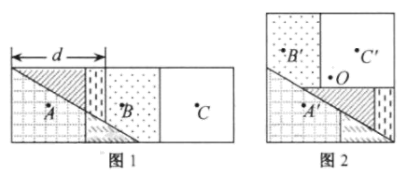
三、解答题(本题有8小题,共80分.解答需写出必要的文字说明、演算步骤或证明过程)
-
17.(1)、计算: .(2)、化简: .18. 如图, 是 的角平分线,在 上取点 ,使 .
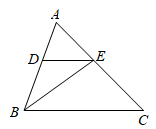 (1)、求证: .(2)、若 , ,求 的度数.19. 某校将学生体质健康测试成绩分为 , , , 四个等级,依次记为4分,3分,2分,1分.为了解学生整体体质健康状况,拟抽样进行统计分析.(1)、以下是两位同学关于抽样方案的对话:
(1)、求证: .(2)、若 , ,求 的度数.19. 某校将学生体质健康测试成绩分为 , , , 四个等级,依次记为4分,3分,2分,1分.为了解学生整体体质健康状况,拟抽样进行统计分析.(1)、以下是两位同学关于抽样方案的对话:小红:“我想随机柚取七年级男、女生各60人的成绩.”
小明:“我想随机柚取七、八、九年级男生各40人的成绩.”
根据右侧学校信息,请你简要评价小红、小明的抽样方案.
如果你来抽取120名学生的测试成绩,请给出抽样方案.
学校共有七、八、九三个年级学生近千人,各段人数相近,每段男、女生人数相当,
.....
(2)、现将随机抽取的测试成绩整理并绘制成如下统计图,请求出这组数据的平均数、中位数和众数.某校部分学生体质健康测试成绩统计图
 20. 如图 与 的方格都是由边长为1的小正方形组成.图1是绘成的七巧板图案,它由7个图形组成,请按以下要求选择其中一个并在图2、图3中画出相应的格点图形(顶点均在格点上).
20. 如图 与 的方格都是由边长为1的小正方形组成.图1是绘成的七巧板图案,它由7个图形组成,请按以下要求选择其中一个并在图2、图3中画出相应的格点图形(顶点均在格点上).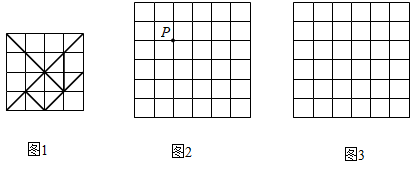 (1)、选一个四边形画在图2中,使点 为它的一个顶点,并画出将它向右平移3个单位后所得的图形.(2)、选一个合适的三角形,将它的各边长扩大到原来的 倍,画在图3中.21. 已知抛物线 经过点 .(1)、求抛物线的函数表达式和顶点坐标.(2)、直线 交抛物线于点 , , 为正数.若点 在抛物线上且在直线 下方(不与点 , 重合),分别求出点 横坐标与纵坐标的取值范围,22. 如图,在 中, , 是对角线 上的两点(点 在点 左侧),且 .
(1)、选一个四边形画在图2中,使点 为它的一个顶点,并画出将它向右平移3个单位后所得的图形.(2)、选一个合适的三角形,将它的各边长扩大到原来的 倍,画在图3中.21. 已知抛物线 经过点 .(1)、求抛物线的函数表达式和顶点坐标.(2)、直线 交抛物线于点 , , 为正数.若点 在抛物线上且在直线 下方(不与点 , 重合),分别求出点 横坐标与纵坐标的取值范围,22. 如图,在 中, , 是对角线 上的两点(点 在点 左侧),且 . (1)、求证:四边形 是平行四边形.(2)、当 , , 时,求 的长.23. 某公司生产的一种营养品信息如下表.已知甲食材每千克的进价是乙食材的2倍,用80元购买的甲食材比用20元购买的乙食材多1千克.
(1)、求证:四边形 是平行四边形.(2)、当 , , 时,求 的长.23. 某公司生产的一种营养品信息如下表.已知甲食材每千克的进价是乙食材的2倍,用80元购买的甲食材比用20元购买的乙食材多1千克.营养品信息表
营养成分
每千克含铁42毫克
配料表
原料
每千克含铁
甲食材
50毫克
乙食材
10毫克
规格
每包食材含量
每包单价
A包装
1千克
45元
B包装
0.25千克
12元
(1)、问甲、乙两种食材每千克进价分别是多少元?(2)、该公司每日用18000元购进甲、乙两种食材并恰好全部用完.①问每日购进甲、乙两种食材各多少千克?
②已知每日其他费用为2000元,且生产的营养品当日全部售出.若A的数量不低于B的数量,则A为多少包时,每日所获总利润最大?最大总利润为多少元?
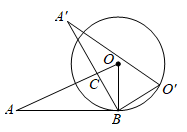
24. 如图,在平面直角坐标系中, 经过原点 ,分别交 轴、 轴于 , ,连结 .直线 分别交 于点 , (点 在左侧),交 轴于点 ,连结 .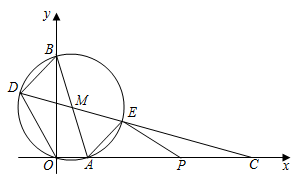 (1)、求 的半径和直线 的函数表达式.(2)、求点 , 的坐标.(3)、点 在线段 上,连结 .当 与 的一个内角相等时,求所有满足条件的 的长.
(1)、求 的半径和直线 的函数表达式.(2)、求点 , 的坐标.(3)、点 在线段 上,连结 .当 与 的一个内角相等时,求所有满足条件的 的长.