浙江省绍兴市2021年中考数学试卷
试卷更新日期:2021-06-22 类型:中考真卷
一、选择题(本大题有10小题,每小题4分,共40分.请选出每小题中一个最符合题意的选项,不选、多选、错选,均不给分)
-
1. 实数2,0,-3, 中,最小的数是( )A、2 B、0 C、-3 D、2. 第七次全国人口普查数据显示,绍兴市常住人口约为5 270 000人,这个数字5270 000用科学记数法可表示为( )A、 B、 C、 D、3. 如图的几何体由五个相同的小正方体搭成,它的主视图是( )
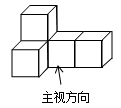 A、
A、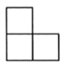 B、
B、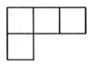 C、
C、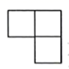 D、
D、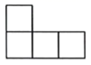 4. 在一个不透明的袋中装有6个只有颜色不同的球,其中3个红球、2个黄球和1个白球.从袋中任意摸出一个球,是白球的概率为( )A、 B、 C、 D、5. 如图,正方形ABCD内接于 ,点P在 上,则 的度数为( )
4. 在一个不透明的袋中装有6个只有颜色不同的球,其中3个红球、2个黄球和1个白球.从袋中任意摸出一个球,是白球的概率为( )A、 B、 C、 D、5. 如图,正方形ABCD内接于 ,点P在 上,则 的度数为( )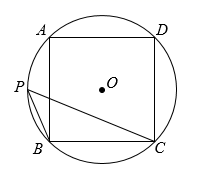 A、 B、 C、 D、6. 关于二次函数 的最大值或最小值,下列说法正确的是( )A、有最大值4 B、有最小值4 C、有最大值6 D、有最小值67. 如图,树AB在路灯O的照射下形成投影AC,已知路灯高 ,树影 ,树AB与路灯O的水平距离 ,则树的高度AB长是( )
A、 B、 C、 D、6. 关于二次函数 的最大值或最小值,下列说法正确的是( )A、有最大值4 B、有最小值4 C、有最大值6 D、有最小值67. 如图,树AB在路灯O的照射下形成投影AC,已知路灯高 ,树影 ,树AB与路灯O的水平距离 ,则树的高度AB长是( )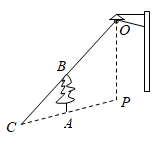 A、 B、 C、 D、8. 如图,菱形ABCD中, ,点P从点B出发,沿折线 方向移动,移动到点D停止.在 形状的变化过程中,依次出现的特殊三角形是( )
A、 B、 C、 D、8. 如图,菱形ABCD中, ,点P从点B出发,沿折线 方向移动,移动到点D停止.在 形状的变化过程中,依次出现的特殊三角形是( )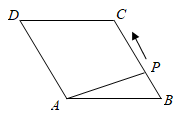 A、直角三角形→等边三角形→等腰三角形→直角三角形 B、直角三角形→等腰三角形→直角三角形→等边三角形 C、直角三角形→等边三角形→直角三角形→等腰三角形 D、等腰三角形→等边三角形→直角三角形→等腰三角形9. 如图, 中, , ,点D是边BC的中点,以AD为底边在其右侧作等腰三角形ADE,使 ,连结CE,则 的值为( )
A、直角三角形→等边三角形→等腰三角形→直角三角形 B、直角三角形→等腰三角形→直角三角形→等边三角形 C、直角三角形→等边三角形→直角三角形→等腰三角形 D、等腰三角形→等边三角形→直角三角形→等腰三角形9. 如图, 中, , ,点D是边BC的中点,以AD为底边在其右侧作等腰三角形ADE,使 ,连结CE,则 的值为( )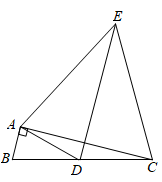 A、 B、 C、 D、210. 数学兴趣小组同学从“中国结”的图案(图1)中发现,用相同的菱形放置,可得到更多的菱形.如图2,用2个相同的菱形放置,得到3个菱形.下面说法正确的是( )
A、 B、 C、 D、210. 数学兴趣小组同学从“中国结”的图案(图1)中发现,用相同的菱形放置,可得到更多的菱形.如图2,用2个相同的菱形放置,得到3个菱形.下面说法正确的是( )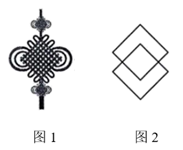 A、用3个相同的菱形放置,最多能得到6个菱形 B、用4个相同的菱形放置,最多能得到16个菱形 C、用5个相同的菱形放置,最多能得到27个菱形 D、用6个相同的菱形放置,最多能得到41个菱形
A、用3个相同的菱形放置,最多能得到6个菱形 B、用4个相同的菱形放置,最多能得到16个菱形 C、用5个相同的菱形放置,最多能得到27个菱形 D、用6个相同的菱形放置,最多能得到41个菱形二、填空题(本大题有6小题,每小题5分,共30分)
-
11. 分解因式:x2+2x+1= .
12. 我国明代数学读本《算法统宗》有一道题,其题意为:客人一起分银子,若每人7两,还剩4两;若每人9两,则差8两,银子共有两.(注:明代时1斤=16两)13. 图1是一种矩形时钟,图2是时钟示意图,时钟数字2的刻度在矩形ABCD的对角线BD上,时钟中心在矩形ABCD对角线的交点O上.若 ,则BC长为cm(结果保留根号).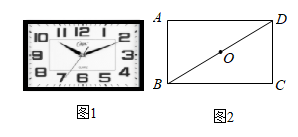 14. 如图,在 中, , ,以点C为圆心,CA长为半径作弧,交直线BC于点P,连结AP,则 的度数是.
14. 如图,在 中, , ,以点C为圆心,CA长为半径作弧,交直线BC于点P,连结AP,则 的度数是.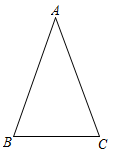 15. 如图,在平面直角坐标系中,正方形ABCD的顶点A在x轴正半轴上,顶点B,C在第一象限,顶点D的坐标 . 反比例函数 (常数 , )的图象恰好经过正方形ABCD的两个顶点,则k的值是.
15. 如图,在平面直角坐标系中,正方形ABCD的顶点A在x轴正半轴上,顶点B,C在第一象限,顶点D的坐标 . 反比例函数 (常数 , )的图象恰好经过正方形ABCD的两个顶点,则k的值是.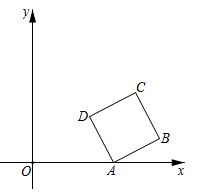 16. 已知 与 在同一平面内,点C,D不重合, , , ,则CD长为.
16. 已知 与 在同一平面内,点C,D不重合, , , ,则CD长为.三、解答题(本大题有8小题,第17~20小题每小题8分,第21小题10分,第22,23小题每小题12分,第24小题14分,共80分.解答需写出必要的文字说明、演算步骤或证明过程)
-
17.(1)、计算: .(2)、解不等式: .18. 绍兴莲花落,又称“莲花乐”,“莲花闹”,是绍兴一带的曲艺.为了解学生对该曲种的熟悉度,某校设置了:非常了解、了解、了解很少、不了解四个选项,随机抽查了部分学生进行问卷调查,要求每名学生只选其中的一项,并将抽查结果绘制成如下不完整的统计图.
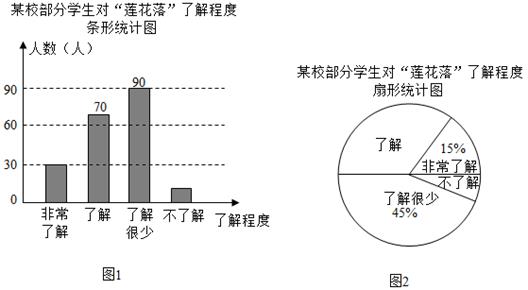
根据图中信息,解答下列问题:
(1)、本次接受问卷调查的学生有多少人?并求图2中“了解”的扇形圆心角的度数.(2)、全校共有1200名学生,请你估计全校学生中“非常了解”、“了解”莲花落的学生共有多少人.19. I号无人机从海拔10m处出发,以10m/min的速度匀速上升,II号无人机从海拔30m处同时出发,以a(m/min)的速度匀速上升,经过5min两架无人机位于同一海拔高度b(m).无人机海拔高度y(m)与时间x(min)的关系如图.两架无人机都上升了15min.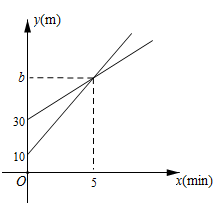 (1)、求b的值及II号无人机海拔高度y(m)与时间x(min)的关系式.(2)、问无人机上升了多少时间,I号无人机比II号无人机高28米.20. 拓展小组研制的智能操作机器人,如图1,水平操作台为l,底座AB固定,高AB为50cm,连杆BC长度为70cm,手臂CD长度为60cm.点B,C是转动点,且AB,BC与CD始终在同一平面内,
(1)、求b的值及II号无人机海拔高度y(m)与时间x(min)的关系式.(2)、问无人机上升了多少时间,I号无人机比II号无人机高28米.20. 拓展小组研制的智能操作机器人,如图1,水平操作台为l,底座AB固定,高AB为50cm,连杆BC长度为70cm,手臂CD长度为60cm.点B,C是转动点,且AB,BC与CD始终在同一平面内,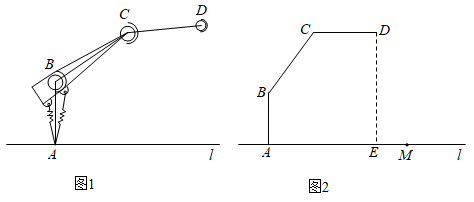 (1)、转动连杆BC,手臂CD,使 , ,如图2,求手臂端点D离操作台 的高度DE的长(精确到1cm,参考数据: , ).(2)、物品在操作台 上,距离底座A端110cm的点M处,转动连杆BC,手臂CD,手臂端点D能否碰到点M?请说明理由.21. 如图,在 中, ,点D,E分別在边AB,AC上, ,连结CD,BE.
(1)、转动连杆BC,手臂CD,使 , ,如图2,求手臂端点D离操作台 的高度DE的长(精确到1cm,参考数据: , ).(2)、物品在操作台 上,距离底座A端110cm的点M处,转动连杆BC,手臂CD,手臂端点D能否碰到点M?请说明理由.21. 如图,在 中, ,点D,E分別在边AB,AC上, ,连结CD,BE.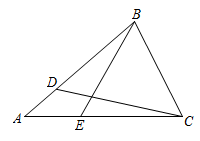 (1)、若 ,求 , 的度数.(2)、写出 与 之间的关系,并说明理由.22. 小聪设计奖杯,从抛物线形状上获得灵感,在平面直角坐标系中画出截面示意图,如图1,杯体ACB是抛物线的一部分,抛物线的顶点C在y轴上,杯口直径 ,且点A,B关于y轴对称,杯脚高 ,杯高 ,杯底MN在x轴上.
(1)、若 ,求 , 的度数.(2)、写出 与 之间的关系,并说明理由.22. 小聪设计奖杯,从抛物线形状上获得灵感,在平面直角坐标系中画出截面示意图,如图1,杯体ACB是抛物线的一部分,抛物线的顶点C在y轴上,杯口直径 ,且点A,B关于y轴对称,杯脚高 ,杯高 ,杯底MN在x轴上.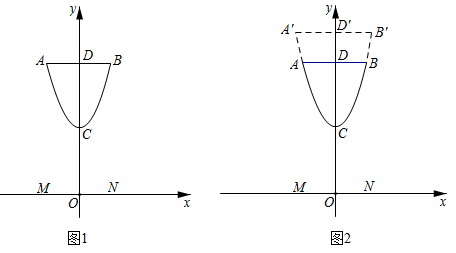 (1)、求杯体ACB所在抛物线的函数表达式(不必写出x的取值范围).(2)、为使奖杯更加美观,小敏提出了改进方案,如图2,杯体 所在抛物线形状不变,杯口直径 ,杯脚高CO不变,杯深 与杯高 之比为0.6,求 的长.23. 问题:如图,在 中, , , , 的平分线AE,BF分别与直线CD交于点E,F,求EF的长.
(1)、求杯体ACB所在抛物线的函数表达式(不必写出x的取值范围).(2)、为使奖杯更加美观,小敏提出了改进方案,如图2,杯体 所在抛物线形状不变,杯口直径 ,杯脚高CO不变,杯深 与杯高 之比为0.6,求 的长.23. 问题:如图,在 中, , , , 的平分线AE,BF分别与直线CD交于点E,F,求EF的长.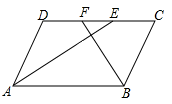
答案: .
(1)、探究:把“问题”中的条件“ ”去掉,其余条件不变.①当点E与点F重合时,求AB的长;
②当点E与点C重合时,求EF的长.
(2)、把“问题”中的条件“ , ”去掉,其余条件不变,当点C,D,E,F相邻两点间的距离相等时,求 的值.24. 如图,矩形ABCD中, ,点E是边AD的中点,点F是对角线BD上一动点, .连结EF,作点D关于直线EF的对称点P.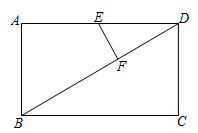 (1)、若 ,求DF的长.(2)、若 ,求DF的长.(3)、直线PE交BD于点Q,若 是锐角三角形,求DF长的取值范围.
(1)、若 ,求DF的长.(2)、若 ,求DF的长.(3)、直线PE交BD于点Q,若 是锐角三角形,求DF长的取值范围.