浙江省宁波市2021年中考数学试卷
试卷更新日期:2021-06-22 类型:中考真卷
一、选择题(每小题4分,共40分.在每小題给出的四个选项中,只有一项符合题目要求)
-
1. 在﹣3,﹣1,0,2这四个数中,最小的数是( )A、﹣3 B、﹣1 C、0 D、22. 计算 的结果是( )A、 B、 C、 D、3. 2021年5月15日,“天问一号”着陆巡视器成功着陆于火星乌托邦平原,此时距离地球约320000000千米.数320000000科学记数法表示为( )A、 B、 C、 D、4. 如图所示的几何体是由一个圆柱和一个长方体组成的,它的主视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 5. 甲、乙、丙、丁四名射击运动员进行射击测试,每人10次射击成绩的平均数 (单位:环)及方差 (单位:环 )如下表所示:
5. 甲、乙、丙、丁四名射击运动员进行射击测试,每人10次射击成绩的平均数 (单位:环)及方差 (单位:环 )如下表所示:甲
乙
丙
丁
9
8
9
9
1.6
0.8
3
0.8
根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应选择( )
A、甲 B、乙 C、丙 D、丁6. 要使分式 有意义,x的取值应满足( )A、 B、 C、 D、7. 如图,在 中, 于点D, .若E,F分别为 , 的中点,则 的长为( )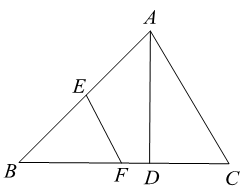 A、 B、 C、1 D、8. 我国古代数学名著《张邱建算经》中记载:“今有清洒一斗直粟十斗,醑酒一斗直粟三斗.今持粟三斛,得酒五斗,问清、醑酒各几何?”意思是:现在一斗清酒价值10斗谷子,一斗醑酒价值3斗谷子,现在拿30斗谷子,共换了5斗酒,问清酒、醑酒各几斗?如果设清酒x斗,醑酒y斗,那么可列方程组为( )A、 B、 C、 D、9. 如图,正比例函数 的图象与反比例函数 的图象相交于A,B两点,点B的横坐标为2,当 时,x的取值范围是( )
A、 B、 C、1 D、8. 我国古代数学名著《张邱建算经》中记载:“今有清洒一斗直粟十斗,醑酒一斗直粟三斗.今持粟三斛,得酒五斗,问清、醑酒各几何?”意思是:现在一斗清酒价值10斗谷子,一斗醑酒价值3斗谷子,现在拿30斗谷子,共换了5斗酒,问清酒、醑酒各几斗?如果设清酒x斗,醑酒y斗,那么可列方程组为( )A、 B、 C、 D、9. 如图,正比例函数 的图象与反比例函数 的图象相交于A,B两点,点B的横坐标为2,当 时,x的取值范围是( )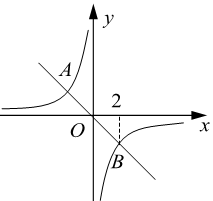 A、 或 B、 或 C、 或 D、 或10. 如图是一个由5张纸片拼成的 ,相邻纸片之间互不重叠也无缝隙,其中两张等腰直角三角形纸片的面积都为 ,另两张直角三角形纸片的面积都为 ,中间一张矩形纸片 的面积为 , 与 相交于点O.当 的面积相等时,下列结论一定成立的是( )
A、 或 B、 或 C、 或 D、 或10. 如图是一个由5张纸片拼成的 ,相邻纸片之间互不重叠也无缝隙,其中两张等腰直角三角形纸片的面积都为 ,另两张直角三角形纸片的面积都为 ,中间一张矩形纸片 的面积为 , 与 相交于点O.当 的面积相等时,下列结论一定成立的是( )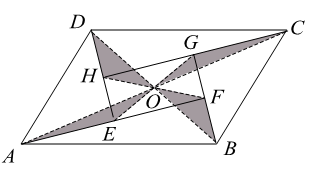 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每小题5分,共30分)
-
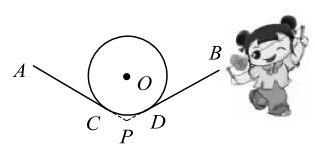
11. 的绝对值是 .12. 分解因式: .13. 一个不透明的袋子里装有3个红球和5个黑球,它们除颜色外其余都相同.从袋中任意摸出一个球是红球的概率为.14. 抖空竹在我国有着悠久的历史,是国家级的非物质文化遗产之一.如示意图, 分别与 相切于点C,D,延长 交于点P.若 , 的半径为 ,则图中 的长为 .(结果保留 )
 15. 在平面直角坐标系中,对于不在坐标轴上的任意一点 ,我们把点 称为点A的“倒数点”.如图,矩形 的顶点C为 ,顶点E在y轴上,函数 的图象与 交于点A.若点B是点A的“倒数点”,且点B在矩形 的一边上,则 的面积为.
15. 在平面直角坐标系中,对于不在坐标轴上的任意一点 ,我们把点 称为点A的“倒数点”.如图,矩形 的顶点C为 ,顶点E在y轴上,函数 的图象与 交于点A.若点B是点A的“倒数点”,且点B在矩形 的一边上,则 的面积为. 16. 如图,在矩形 中,点E在边 上, 与 关于直线 对称,点B的对称点F在边 上,G为 中点,连结 分别与 交于M,N两点,若 , ,则 的长为 , 的值为.
16. 如图,在矩形 中,点E在边 上, 与 关于直线 对称,点B的对称点F在边 上,G为 中点,连结 分别与 交于M,N两点,若 , ,则 的长为 , 的值为.
三、解答题(本大题有8小题,共80分)
-
17.(1)、计算: .(2)、解不等式组: .18. 如图是由边长为1的小正方形构成的 的网格,点A,B均在格点上.
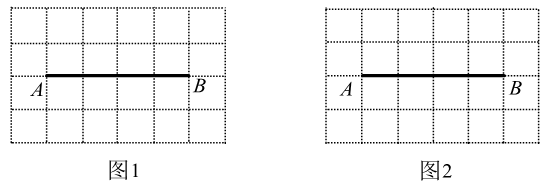 (1)、在图1中画出以 为边且周长为无理数的 ,且点C和点D均在格点上(画出一个即可).(2)、在图2中画出以 为对角线的正方形 ,且点E和点F均在格点上.19. 如图,二次函数 (a为常数)的图象的对称轴为直线 .
(1)、在图1中画出以 为边且周长为无理数的 ,且点C和点D均在格点上(画出一个即可).(2)、在图2中画出以 为对角线的正方形 ,且点E和点F均在格点上.19. 如图,二次函数 (a为常数)的图象的对称轴为直线 . (1)、求a的值.(2)、向下平移该二次函数的图象,使其经过原点,求平移后图象所对应的二次函数的表达式.20. 图1表示的是某书店今年1~5月的各月营业总额的情况,图2表示的是该书店“党史”类书籍的各月营业额占书店当月营业总额的百分比情况.若该书店1~5月的营业总额一共是182万元,观察图1、图2,解答下列向题:
(1)、求a的值.(2)、向下平移该二次函数的图象,使其经过原点,求平移后图象所对应的二次函数的表达式.20. 图1表示的是某书店今年1~5月的各月营业总额的情况,图2表示的是该书店“党史”类书籍的各月营业额占书店当月营业总额的百分比情况.若该书店1~5月的营业总额一共是182万元,观察图1、图2,解答下列向题: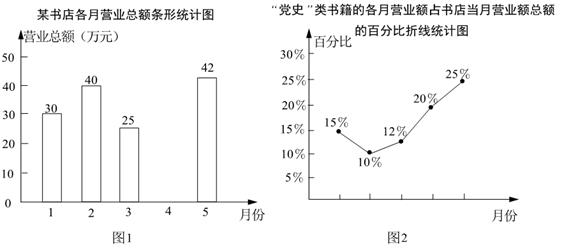 (1)、求该书店4月份的营业总额,并补全条形统计图.(2)、求5月份“党史”类书籍的营业额.(3)、请你判断这5个月中哪个月“党史”类书籍的营业额最高,并说明理由.21. 我国纸伞的制作工艺十分巧妙.如图1,伞不管是张开还是收拢,伞柄 始终平分同一平面内两条伞骨所成的角 ,且 ,从而保证伞圈D能沿着伞柄滑动.如图2是伞完全收拢时伞骨的示意图,此时伞圈D已滑动到点 的位置,且A,B, 三点共线, ,B为 中点,当 时,伞完全张开.
(1)、求该书店4月份的营业总额,并补全条形统计图.(2)、求5月份“党史”类书籍的营业额.(3)、请你判断这5个月中哪个月“党史”类书籍的营业额最高,并说明理由.21. 我国纸伞的制作工艺十分巧妙.如图1,伞不管是张开还是收拢,伞柄 始终平分同一平面内两条伞骨所成的角 ,且 ,从而保证伞圈D能沿着伞柄滑动.如图2是伞完全收拢时伞骨的示意图,此时伞圈D已滑动到点 的位置,且A,B, 三点共线, ,B为 中点,当 时,伞完全张开. (1)、求 的长.(2)、当伞从完全张开到完全收拢,求伞圈D沿着伞柄向下滑动的距离.(参考数据: )22. 某通讯公司就手机流量套餐推出三种方案,如下表:
(1)、求 的长.(2)、当伞从完全张开到完全收拢,求伞圈D沿着伞柄向下滑动的距离.(参考数据: )22. 某通讯公司就手机流量套餐推出三种方案,如下表:A方案
B方案
C方案
每月基本费用(元)
20
56
266
每月免费使用流量(兆)
1024
m
无限
超出后每兆收费(元)
n
n
A,B,C三种方案每月所需的费用y(元)与每月使用的流量x(兆)之间的函数关系如图所示.
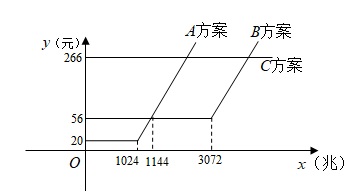 (1)、请直接写出m,n的值.(2)、在A方案中,当每月使用的流量不少于1024兆时,求每月所需的费用y(元)与每月使用的流量x(兆)之间的函数关系式.(3)、在这三种方案中,当每月使用的流量超过多少兆时,选择C方案最划算?23. 如图
(1)、请直接写出m,n的值.(2)、在A方案中,当每月使用的流量不少于1024兆时,求每月所需的费用y(元)与每月使用的流量x(兆)之间的函数关系式.(3)、在这三种方案中,当每月使用的流量超过多少兆时,选择C方案最划算?23. 如图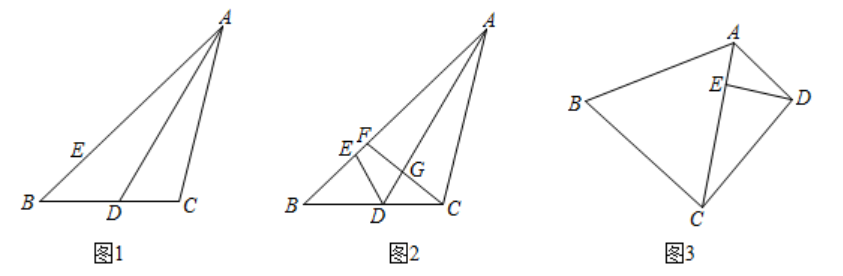 (1)、(证明体验)
(1)、(证明体验)如图1, 为 的角平分线, ,点E在 上, .求证: 平分 .
(2)、(思考探究)如图2,在(1)的条件下,F为 上一点,连结 交 于点G.若 , , ,求 的长.
(3)、(拓展延伸)如图3,在四边形 中,对角线 平分 ,点E在 上, .若 ,求 的长.
24. 如图1,四边形 内接于 , 为直径, 上存在点E,满足 ,连结 并延长交 的延长线于点F, 与 交于点G.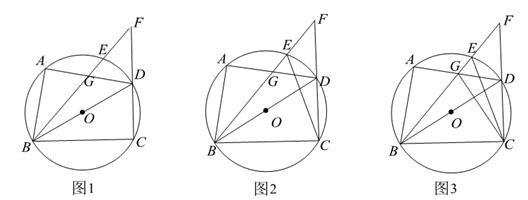 (1)、若 ,请用含 的代数式表列 .(2)、如图2,连结 .求证; .(3)、如图3,在(2)的条件下,连结 , .
(1)、若 ,请用含 的代数式表列 .(2)、如图2,连结 .求证; .(3)、如图3,在(2)的条件下,连结 , .①若 ,求 的周长.
②求 的最小值.