浙江省金华市2021年中考数学试卷
试卷更新日期:2021-06-22 类型:中考真卷
一、一、选择题(本题有10小题,每小题3分,共30分
-
1. 实数 , ,2,-3中,为负整数的是( )A、 B、 C、2 D、-32. ( )A、3 B、 C、 D、3. 据科学家估计,太阳与地球的平均距离大约是 千米,现将数字 用科学记数法表示应为( )A、 B、 C、 D、4. 一个不等式的解在数轴上表示如图,则这个不等式可以是( )
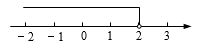 A、 B、 C、 D、5. 某同学的作业如下框,其中※处填的依据是( )
A、 B、 C、 D、5. 某同学的作业如下框,其中※处填的依据是( )如图,已知直线 .若 ,则 .
请完成下面的说理过程.
解:已知 ,
根据(内错角相等,两直线平行),得 .
再根据( ※ ),得 .
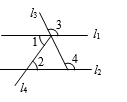 A、两直线平行,内错角相等 B、内错角相等,两直线平行 C、两直线平行,同位角相等 D、两直线平行,同旁内角互补6. 将如图所示的直棱柱展开,下列各示意图中不可能是它的表面展开图的是( )
A、两直线平行,内错角相等 B、内错角相等,两直线平行 C、两直线平行,同位角相等 D、两直线平行,同旁内角互补6. 将如图所示的直棱柱展开,下列各示意图中不可能是它的表面展开图的是( )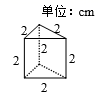 A、
A、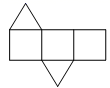 B、
B、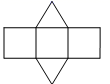 C、
C、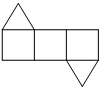 D、
D、 7. 如图是一架人字梯,已知 米,AC与地面BC的夹角为 ,则两梯脚之间的距离BC为( )
7. 如图是一架人字梯,已知 米,AC与地面BC的夹角为 ,则两梯脚之间的距离BC为( )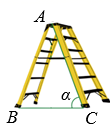 A、 米 B、 米 C、 米 D、 米8. 已知点 在反比例函数 的图象上.若 ,则( )A、 B、 C、 D、9. 某超市出售一商品,有如下四种在原标价基础上调价的方案,其中调价后售价最低的是( )A、先打九五折,再打九五折 B、先提价 ,再打六折 C、先提价 ,再降价 D、先提价 ,再降价10. 如图,在 中, ,以该三角形的三条边为边向形外作正方形,正方形的顶点 都在同一个圆上.记该圆面积为 , 面积为 ,则 的值是( )
A、 米 B、 米 C、 米 D、 米8. 已知点 在反比例函数 的图象上.若 ,则( )A、 B、 C、 D、9. 某超市出售一商品,有如下四种在原标价基础上调价的方案,其中调价后售价最低的是( )A、先打九五折,再打九五折 B、先提价 ,再打六折 C、先提价 ,再降价 D、先提价 ,再降价10. 如图,在 中, ,以该三角形的三条边为边向形外作正方形,正方形的顶点 都在同一个圆上.记该圆面积为 , 面积为 ,则 的值是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题 (本题有6小题,每小题4分,共24分
-
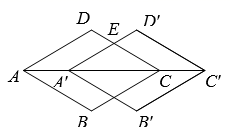
11. 二次根式 中,x的取值范围是 .12. 已知 是方程 的一个解,则m的值是.13. 某单位组织抽奖活动,共准备了150张奖券,设一等奖5个,二等奖20个,三等奖80个.已知每张奖券获奖的可能性相同,则1张奖券中一等奖的概率是.14. 如图,菱形 的边长为 , ,将该菱形沿AC方向平移 得到四边形 , 交CD于点E,则点E到AC的距离为 .
 15. 如图,在平面直角坐标系中,有一只用七巧板拼成的“猫”,三角形①的边BC及四边形②的边CD都在x轴上,“猫”耳尖E在y轴上.若“猫”尾巴尖A的横坐标是1,则“猫”爪尖F的坐标是.
15. 如图,在平面直角坐标系中,有一只用七巧板拼成的“猫”,三角形①的边BC及四边形②的边CD都在x轴上,“猫”耳尖E在y轴上.若“猫”尾巴尖A的横坐标是1,则“猫”爪尖F的坐标是.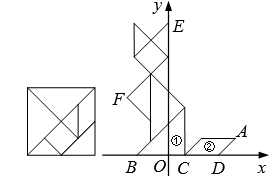 16. 如图1是一种利用镜面反射,放大微小变化的装置.木条BC上的点P处安装一平面镜,BC与刻度尺边MN的交点为D,从A点发出的光束经平面镜P反射后,在MN上形成一个光点E.已知 , .
16. 如图1是一种利用镜面反射,放大微小变化的装置.木条BC上的点P处安装一平面镜,BC与刻度尺边MN的交点为D,从A点发出的光束经平面镜P反射后,在MN上形成一个光点E.已知 , .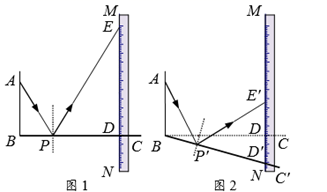 (1)、ED的长为.(2)、将木条BC绕点B按顺时针方向旋转一定角度得到 (如图2),点P的对应点为 , 与MN的交点为D′,从A点发出的光束经平面镜 反射后,在MN上的光点为 .若 ,则 的长为.
(1)、ED的长为.(2)、将木条BC绕点B按顺时针方向旋转一定角度得到 (如图2),点P的对应点为 , 与MN的交点为D′,从A点发出的光束经平面镜 反射后,在MN上的光点为 .若 ,则 的长为.三、解答题 (本题有8小题,共66分,各小题都必须写出解答过程
-
17. 计算: .18. 已知 ,求 的值.19. 已知:如图,矩形 的对角线 相交于点O, .
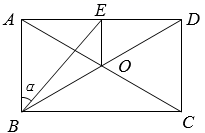 (1)、求矩形对角线的长.(2)、过O作 于点E,连结BE.记 ,求 的值.20. 小聪、小明准备代表班级参加学校“党史知识”竞赛,班主任对这两名同学测试了6次,获得如下测试成绩折线统计图.根据图中信息,解答下列问题:
(1)、求矩形对角线的长.(2)、过O作 于点E,连结BE.记 ,求 的值.20. 小聪、小明准备代表班级参加学校“党史知识”竞赛,班主任对这两名同学测试了6次,获得如下测试成绩折线统计图.根据图中信息,解答下列问题: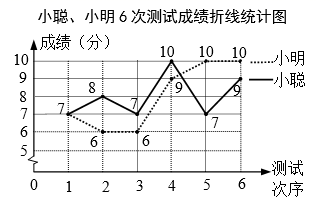 (1)、要评价每位同学成绩的平均水平,你选择什么统计量?求这个统计量.(2)、求小聪成绩的方差.(3)、现求得小明成绩的方差为 (单位:平方分).根据折线统计图及上面两小题的计算,你认为哪位同学的成绩较好?请简述理由.21. 某游乐场的圆形喷水池中心O有一雕塑OA,从A点向四周喷水,喷出的水柱为抛物线,且形状相同.如图,以水平方向为x轴,点O为原点建立直角坐标系,点A在y轴上,x轴上的点C,D为水柱的落水点,水柱所在抛物线第一象限部分的函数表达式为 .
(1)、要评价每位同学成绩的平均水平,你选择什么统计量?求这个统计量.(2)、求小聪成绩的方差.(3)、现求得小明成绩的方差为 (单位:平方分).根据折线统计图及上面两小题的计算,你认为哪位同学的成绩较好?请简述理由.21. 某游乐场的圆形喷水池中心O有一雕塑OA,从A点向四周喷水,喷出的水柱为抛物线,且形状相同.如图,以水平方向为x轴,点O为原点建立直角坐标系,点A在y轴上,x轴上的点C,D为水柱的落水点,水柱所在抛物线第一象限部分的函数表达式为 . (1)、求雕塑高OA.(2)、求落水点C,D之间的距离.(3)、若需要在OD上的点E处竖立雕塑EF, , .问:顶部F是否会碰到水柱?请通过计算说明.22. 在扇形 中,半径 ,点P在OA上,连结PB,将 沿PB折叠得到 .
(1)、求雕塑高OA.(2)、求落水点C,D之间的距离.(3)、若需要在OD上的点E处竖立雕塑EF, , .问:顶部F是否会碰到水柱?请通过计算说明.22. 在扇形 中,半径 ,点P在OA上,连结PB,将 沿PB折叠得到 .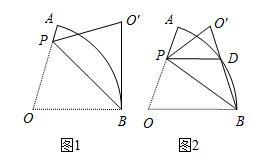 (1)、如图1,若 ,且 与 所在的圆相切于点B.
(1)、如图1,若 ,且 与 所在的圆相切于点B.①求 的度数.
②求AP的长.
(2)、如图2, 与 相交于点D,若点D为 的中点,且 ,求 的长.23. 背景:点A在反比例函数 的图象上, 轴于点B, 轴于点C,分别在射线 上取点 ,使得四边形 为正方形.如图1,点A在第一象限内,当 时,小李测得 .探究:通过改变点A的位置,小李发现点D,A的横坐标之间存在函数关系.请帮助小李解决下列问题.
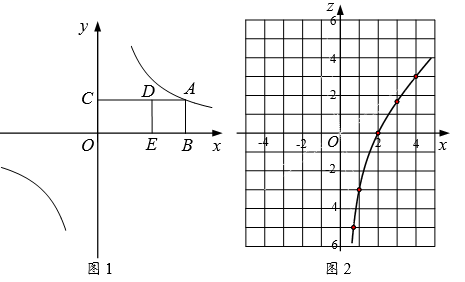 (1)、求k的值.(2)、设点 的横坐标分别为 ,将z关于x的函数称为“Z函数”.如图2,小李画出了 时“Z函数”的图象.
(1)、求k的值.(2)、设点 的横坐标分别为 ,将z关于x的函数称为“Z函数”.如图2,小李画出了 时“Z函数”的图象.①求这个“Z函数”的表达式.
②补画 时“Z函数”的图象,并写出这个函数的性质(两条即可).
③过点 作一直线,与这个“Z函数”图象仅有一个交点,求该交点的横坐标.
24. 在平面直角坐标系中,点A的坐标为 ,点B在直线 上,过点B作AB的垂线,过原点O作直线l的垂线,两垂线相交于点C.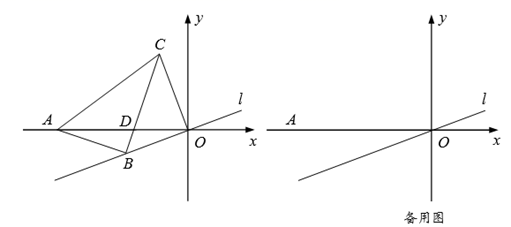 (1)、如图,点B,C分别在第三、二象限内,BC与AO相交于点D.
(1)、如图,点B,C分别在第三、二象限内,BC与AO相交于点D.①若 ,求证: .
②若 ,求四边形 的面积.
(2)、是否存在点B,使得以 为顶点的三角形与 相似?若存在,求OB的长;若不存在,请说明理由.